艾里函数的完备约化系统

杜昊^1,2,*, Clemens G.Raab³

(1. 北京邮电大学理学院, 北京 102206
2. 教育部数学与信息网络重点实验室, 北京 102206
3. 约翰·开普勒 (林茨) 大学代数教研室, 林茨 4040. )

摘要: 计算某种“闭形式”的不定积分,即符号积分,是计算机代数的一个重要研究领域。在部分实现递归Risch算法后,人们发现并行积分方法可以实现更高效的算法,其中最著名的算法之一是Risch-Norman算法。然而,这种方法依赖于积分中无法准确得到的多项式次数的估计。Norman基于完备化思想提供了一种避免次数估计的替代方法。然而,根据微分域的构造和项序的选择,可能会发生完备化过程不能终止并产生无限多约化法则的情况。我们将Norman方法优化并应用于在物理学中有重要应用的Airy函数生成的微分环。通过确定适当的项序,我们用有限个公式表示无限多个约化法则,并给出了Airy函数的两个完备约化系统。

关键词: 符号积分, Risch-Norman算法, 无限约化系统

DOI: 10.48014/bcam.20230724002

引用格式: 杜昊,Clemens Raab. 艾里函数的完备约化系统[J]. 中国应用数学通报,2023,1(1):10-22.

文章类型: 研究性论文

收稿日期: 2023-07-24

接收日期: 2023-08-28

出版日期: 2023-12-28

1　Introduction

Symbolic integration is used to calculate certain“closed form” of integrals by algebraic methods.Traditionally，algorithms using differential fields have been developed for that，see e.g.[22，5，20].Nowadays，symbolic integration based on reduction becomes popular，especially when creative telescoping plays an important role [3，1，8，9，2，16，7，12].It also has many applications in combinatorics，algorithm complexity analysis and mathematical physics，see [25] for example.

Liouville’s Theorem and its various refinements on the structure of elementary integrals are the main theoretical foundation for many algorithms in symbolic integration.Basically，Liouville’s Theorem tells that a rational expression f in terms of given functions y_i has an integral that is an elementary expression of the y_i if and only if it has an integral of the form

∫f=+α_iln，

where α_i are constants and u，v，p_iare polynomial expressions in the y_i or，in other words，f can be written as

f=+α_i.

Risch [22，23] developed an algorithm to determine whether an elementary function has an elementary integral.Main parts of the algorithm are also presented in [15，5].See [24] for commentaries and details as well as further developments and references.Since these algorithms are very involved because of their recursive structure，a simpler and more efficient approach was devised:the Risch-Norman algorithm [19].It aims at directly finding candidates for polynomials v and p_i and determining u and α_i in the above form of the integral.Since in general this approach relies on heuristics so far，it may fail to find an elementary integral even if the given integrand has one.Nonetheless，the approach is powerful in practice，rather easy to implement，and can even be generalized to many classes of integrands for which no other algorithm is available.For details，see [14] and [5，Ch.10]，for example.We will discuss how to find the numerator u later.

For instance，Boettner observed that the following antiderivative cannot be found by recent extensions of the Risch—Norman algorithm[4，Ex.8.7].

∫Ai'(x)²dx=Ai'(x)²+

Ai(x)Ai'(x)-Ai(x)² (1)

The Airy function Ai(x)satisfies Ai″=xAi

and can be given by the integral

Ai=cosdt

for real x.Its properties and applications in physics are discussed in [26] and [11，Ch.9]，for example.

Norman [18] proposed improvements to make the heuristic Risch-Norman algorithm more powerful by addressing the problem of finding the numerator of the rational part of the integral.Instead of finding u via an ansatz with undetermined constant coefficients as explained above，he discussed a reduction-based approach to this problem.His reduction rules are based on identities for fixed v relating certain numerators u with the corresponding integrands，such as

∫f= or f=，

which involve parameters in their coefficients and exponents.To reduce a given term，an instance f as above used for reducing can only be multiplied by a constant coefficient to match its leading term with the given term.In this paper，based on Norman’s completion-based approach [18]，we present two complete reduction systems for Airy functions which are both infinite.

2　Preliminaries

Let F be a field of characteristic zero.A derivation ∂ on F is an additive map that satisfies the product rule ∂=g+f for all f，g∈F.Then forms a differential field.The set of constant elements in F forms a subfield denoted by Const_∂=.

Moreover，we only consider the case where the field F is given as a purely transcendental extension F=C of a field of constants C⊆ Const_∂(F) by elements t₁，...，t_n∈F that are algebraically independent over C.Hence，∂ is a C-linear map on the multivariate rational function field C and t₁，…，t_n model algebraically independent functions.

Actually，a derivation on such a field is completely determined by the elements ∂t₁，…，∂t_n via ∂=·∂_i，where ∂_i is the standard partial derivation with respect to t_i.Conversely，any choice of ∂t₁，…，∂t_n∈F yields a derivation on F this way.The following definition is based on [5，Ch.10].

Definition.For = with C⊆Const_∂ such that t₁，…，t_n are algebraically independent over C，we define the denominator of ∂ as den:=lcm and to ∂ we associate the derivation :F→F defined by f:=den·∂f.

In contrast to∂，the derivation necessarily maps polynomials to polynomials so that is a differential subring of .

2.1　Elementary integrals

In order to discuss elementary integration，we recall several notions in the following，see e.g.[5，Ch.3].Let and be two differential fields.We say that E is a differential field extension of F，or F is a differential subfield of E，if E contains F and =∂.When there is no confusion，we still denote the derivation Δ on E by ∂.Let t belong to a differential extension of F.Then，t is called a monomial over F if it is transcendental over F and its derivative belongs to F.It is called exponential over F，if its logarithmic derivative is equal to the derivative of some element in F;and is said to be logarithmic over F if its derivative is equal to the logarithmic derivative of some element in F.For example，exp(x)is exponential over C(x)with the usual derivation ，because exp(x)'/ exp(x)= 1 is the derivative of x;similarly，log is logarithmic over C(x)by log'=.

We call an elementary extension of if there are z₁，…，z_n∈E such that E=F and z_i is exponential，logarithmic，or algebraic over for all i=1，2，…，n.Then，we say f∈F has an elementary integral，if there is an elementary extension of and g∈E such that f=∂g，and we call such g an elementary integral of f.

For a field= as above，the Risch-Norman algorithm mentioned earlier first determines polynomials v∈Candp₁，…，p_m∈C and then solves the ansatz

f=∂+α_i(2)

for α₁，…，α_m∈C and the constant coefficients of u∈C，where the potential support of u is chosen based on heuristic degree bounds.Only for differential fields of certain type，theoretical results predict how v and p₁，…，p_m have to be chosen explicitly in order not to miss any solutions，see [10，13] and also [5，Sec.10.4].In particular，there is the well-known case of rational function integration corresponding to with ∂t₁=1，where even a comprehensive choice of candidate monomials appearing in u can be given based on f.

Determining u is challenging because of possible cancellations in the derivative ∂u.In practice，usually various heuristic degree bounds have been used to determine a finite ansatz for u.In the literature，the bound

(u)≤1-min(1，(∂t_i))+
max((num(f))，(den(f)))(3)

on partial degrees is given for elementary F，cf.[14，5]，and in general [5] proposes to use the following bound on the total degree.

deg(u)≤1+deg(num(f))+
max(0，deg- deg)(4)

In implementations，the bounds

deg(u)≤1+deg+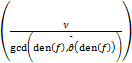
max(5)

on the total degree [6] and

(u)≤1+max，

+

(6)

on the partial degrees [4] have been used.

Example 1.For the integral(1)，we consider the differential field with ∂t₁=1，∂t₂= t₃，and ∂t₃= t₁t₂.The generators t₁，t₂，t₃ correspond to the functions x，Ai，and Ai'，respectively.In the notation of(2)，we havef= ，i.e.m=0.The integral is given by

u=t₁+t₂t₃-(7)

and v = 1.Note that this integral violates all degree bounds(3)—(6)mentioned above.

Thus，we are going to apply an alternative approach to find the numerator u of the integral by reduction.This idea comes from [18].When v and p_i in(2)are given，determining whether the integrand f∈C has an elementary integral can be done by reducing it using a sufficiently complete set of known terms ∂ coming from known q_i∈C that generate the whole space {∂(q/v)|q∈C[t₁，…，t_n]}.Such pairs can be found via a completion procedure proposed by Norman starting from pairs where q_i is just a monomial.

2.2　Monomial orders

Usually，a semigroup order on the commutative monoid of monomials is called a monomial order if it satisfies t_i>1 for all i.Monomial orders can be induced by matrices acting on exponent vectors of monomials.A monomial order is called lexicographic if it can be induced by a permutation matrix.More generally，a monomial order is called a block order if it can be induced by a matrix which is(up to permutation of columns)a block diagonal matrix.

Example 2.Compare the ordering of monomials t₁t₃，t₂t₃，t₁， and t₁t₂t₃，which are shown together with the images of their exponent vectors after applying the matrices below.

1. With the block order induced by ，we have

2. With the order induced by ，we have

Moreover，these orders are going to be used later.

3　Reduction systems for Airy functions

Let Ai be the Airy function，which satisfies the second order differential equation y″=xy.Assume that

∂t₁=1，∂t₂=t₃ and ∂t₃=t₁t₂.

Then t₁ can be viewed as x，t₂ can be viewed as Ai and t₃ can be viewed as the derivative of Ai.In addition， is the minimal differential field containing the rational functions，the Airy function and any order of its derivatives.

Throughout this section，we consider the differential ring C with the derivation ∂，because the least common denominator of the derivatives of generators is equal to 1.In order to simplify the integrability problem of an element in C，we restrict to integrating polynomials.Then we can prove that if a polynomial has an elementary integral，then the integral should also be a polynomial in C. Define θ:=，then C is a tower of monomial extensions since ∂θ=-θ²+t₁ and ∂t₂=θt₂.

Theorem 1.If a polynomial f∈C has an elementary integral over ，then there exists g∈C such that ∂g=f.

Proof.From Lemma 2 below，it follows that there is no polynomial p∈C\C with ∈C.Therefore，the claim follows from Theorem 10.2.1 of [5].

In the following two lemmas，we follow the convention to say a polynomial is special if it divides its own derivative.

Lemma 1.There are no special polynomials in C(t₁)[θ]\C(t₁) and we have Const(C(t₁，t₂，t₃))=C.

Proof.It was shown in [17，Sec.2.2] that the Airy differential equation ∂²y-t₁y=0 has no non-zero Liouvillian solutions.Consequently^[③]，∂y=-y²+t₁ does not have an algebraic solution ω∈，since expwould be a Liouvillian solution of the Airy differential equation.Then，by Theorem 3.4.3 of [5]，there is no special polynomial in C\C.Now，Corollary 2.54 of [20] yields Const=C.

Lemma 2.Let p，q∈C such that ∂p=q·p and p≠0，then p，q∈C.

Proof.By Lemma 1，we have Const=C.Therefore，by homogeneity of ∂ w.r.t.total degree in t₂，t₃，we have either deg(p)= 0 or deg=deg(p).Together，this implies q∈C.Hence，by homogeneity of ∂，each homogeneous part h of p satisfies ∂h=qh.Let h=f with f∈C and n = deg(p)be the leading homogeneous part of p.Then，we obtain ∂h=+nθf，which implies ∂f=f， i.e.f∈C is a special polynomial.By Lemma 1，we obtain f∈C.Thus，n=0 follows from ∂f=f，which implies p∈C.

Next，we are going to present two complete reduction systems for Airy functions with respect to different monomial orders.A reduction system can be viewed as a set of polynomial pairs∈C such that ∂q=p with p monic.It is said to be complete if the leading monomial of ∂f for any f∈C can be reduced by some pair in the system，i.e.，the leading monomial of ∂f is equal to the leading monomial of p in the pair.In principle，complete reduction systems can be computed by the method presented in [18].However，the algorithm may not terminate and produce infinitely many parameterized formulas for such pairs，which is the case in the situations below.It turns out that a subset of these formulas，which still is infinite，is sufficient to define a complete reduction system.We describe the pattern of these sufficient reduction rules in the concrete cases.

3.1　A reduction system based on a block order

In this subsection，we show a complete reduction system based on the block order induced by .The main reason to choose such an order is because for any polynomial p∈C，the total degree in t₂ and t₃ of p is equal to that of the derivative of p.So we try to use a block ordering to determine the leading term of polynomials:first use a degree reverse lexicographic order with t₂<t₃，then compare the degree of t₁.

Then due to the above monomial order，we find reduction rules as follows.

Theorem 2.(i) For all i，j，k∈Ν with k≥1，we have

∂=+

.

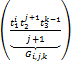(ii) For all i，j，k∈Ν with i≥-，there is

P_i，j，k=c_m，n

with c_m，n∈C depending on i，j，k such that P_i，j，k∈C and

∂P_i，j，k=+

.

with a_m，b_m ∈ C depending on i，j，k.

Proof.(i)It follows from the product rule.

(ii)We proceed by induction on j.If j=0，then we can find

P_i，0，k= and ∂P_i，0，k=+t₂.

If j=1，we can find

P_i，1，k=-t₂+ and

∂P_i，1，k=t₂--

，

which match the conditions.Then we assume thatj≥2 and that (ii) holds for j-1.Note that

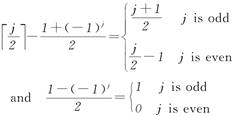(8)

First assume j is odd.Then by the induction hypothesis，there exists P_{i-2，j-1，k+1} in C with i-2≥-1，which implies that i≥，such that

P_{i-2，j-1，k+1}=c_m，n

and its derivative equals to

+a_m+

　b_m. (9)

According to the generic reduction rule(i)，for all m∈Ν，i≥3m+2，j∈Z⁺ and k∈Ν，we have that ∂G_{i-3m-2，j-1，k+1}equals

++
　.

For the following construction，one can note that i≥ does not imply i≥3m+2，but all coefficients a_m of monomials with negative powers of t₁ are zero anyway since ∂P_{i-2，j-1，k+1}∈C.In order to cancel the monomials containing ，let

P_i，j，k=·

P_{i-2，j-1，k+1}-G_{i-2，j-1，k+1}-

a_mG_{i-3m-2，j-1，k+1}

=+

=

+

=

with a₀=1，so that the derivative of P_i，j，k is equal to

++，

where ， and depend on the coefficients a_m，b_m and c_m，n in (9) as well as on the exponents i，j，k.Thus，P_i，j，k and ∂P_i，j，k satisfy the form in (ii)，which implies that the theorem holds for the odd case.

Next assume that j is even.By the induction hypothesis，there exists

P_{i+1，j-1，k+1}=c_m，n

with i+1≥ by (8)，which implies i≥-1，such that its derivative is equal to

+a_m+

　b_m，

wherea_m，b_m and c_m，ndepend on i+1，j-1 and k+1.Let a₀=1 and

P_i，j，k=·

P_{i+1，j-1，k+1}-a_mG_{i-3m+1，j-1，k+1}.

Then similarly，we can check that both P_i，j，k and ∂P_i，j，k satisfy the form given in the theorem，which implies the even case holds，too.

However，it is difficult to express the coefficients of the reduction rules as in the statement of the theorem above.Actually，the reduction rules can be created by the recurrence

，

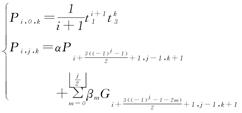where the coefficients α and β_m depend on i，j，k and satisfy some linear system such that all of the coefficients of appearing in ∂P_i，j，k are equal to zero.So it is hard to use these rules in practice.We do not present a completeness proof for this reduction system since the proof is similar to the proof of Theorem 4 in the next subsection.

3.2　A reduction system based on an adapted

order

The reduction system shown above contains complicated coefficients which satisfy some recurrences.This gives us a great difficulty to create reduction rules efficiently.So we try to use a different monomial order，which is induced by to see whether there are some improvements.The order follows from the fact that the weighted degree with respect to (2，0，1) of the leading monomial of ∂G_i，j，k as in Theorem 2(i)is equal to another monomial in the lower terms.In order to keep the completeness of the reduction system，we repeat the generic reduction rule as shown in Theorem 2(i)in the following theorem and then present new reduction rules due to the new monomial order.

Theorem 3.(i) For all i，j，k∈Ν with k≥1，we have

∂=+

.

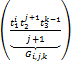(ii) For all i，j∈Ν with j being odd and i≥，there is

=!!

with the leading monomial ·，such that

∂=+

.

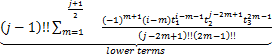(iii) For all i，j∈Ν with j being even and i≥-1，there is

=c_j，0(t₁-+c_j，m

with the leading monomial such that

∂=+，

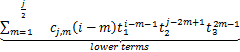where c_j，m∈C with

c_j，0=

and

=(-1c_j，0.

Moreover，there is a× matrix A equaling

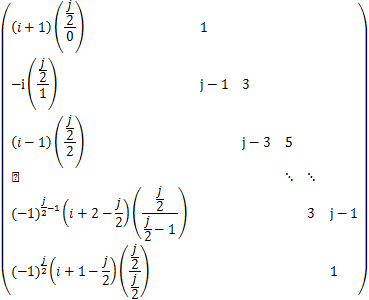
such that

A·=.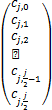

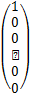Proof.(i)and(ii)follow from the product rule.

(iii)It is easy to check that

∂=+

+

+

((j-2m+1)c_j，m+

(2m+1)c_j，m+1)+

c_j，m.

We denote the above matrix by A= with

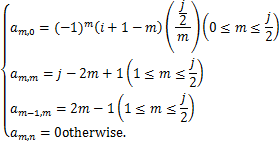
Then by the Laplace expansion with respect to the first column of A，

det=!!

!!.

It follows from Wilf-Zeilberger method that the following identities are satisfied for all nonnegative integers n，in particular，setting n=，

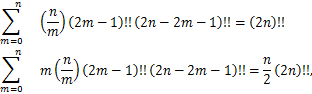
which implies det= is nonzero.Thus，we can find a unique nonzero solution of the linear system A·= ，such that

∂=+c_j，m.

In particular，c_j，0=，where A_1，1=!! is the -cofactor of A，and =c_j，0.

Then the above reduction rules can be easily built up due to linear algebra.Next，we verify the completeness of the above reduction system，i.e.，explain that the monomials which do not satisfy the conditions shown in Theorem 3(i)，(ii)and(iii)cannot be equal to the leading monomial of any derivative.

Theorem 4.A nonzero polynomial in C whose support contains only monomials of the form such that i≤-2 for even j，and i≤ for odd j，does not have an antiderivative in C.

Proof.It is sufficient to consider only monomials where j+k=d is the same.So，we let p，q₀，…，q_d∈C[t₁] such that p=∂q，where

q:=q_j.

For d=0，all nonzero polynomials have an integral since p=∂q reduces to the identity p=∂q₀ in C and we have ∂t₁=1.Correspondingly，no monomial with i≤-2 exists in C for d=0.

Now，let d ≥ 1.First，we assume q₀=0.Let j∈ be minimal such that q_j≠0.Then，the part of ∂q containing is given by jq_j，which is nonzero in contradiction to p=∂q.It follows that q=0 and hence p=0.

Now，we assumeq₀≠0 and let l:=deg.Without loss of generality，we can assume that q₀ is monic(otherwise we modify p and all q_j by dividing them by lc(q₀)).Next，we inductively prove the following properties of q_j for all j∈.

1. If j is even，then

deg=l+ and coeff>0.

2. If j is odd，then

deg≤l+ and coeff≥0.

Forj=0，we have deg=l and coeff(q₀，)>0 by definition.For j=1，the part of ∂q containing is given by +q₁，which is zero by p=∂q.Hence，q₁=-∂q₀ has deg≤l-1 and coeff≥0，even if l=0.For j≥2，the part of ∂q containing is given by

q_j-2t₁++jq_j，which is zero by p=∂q.Therefore，

q_j=-.

If j is even，then we have

deg≤l+<l+=deg+2

by the induction hypothesis.Consequently，we obtain

deg=deg+1=l+

as well as

coeff=-

coeff>0

by the induction hypothesis.On the other hand，if j is odd，we have deg=l+≥deg+2 by the induction hypothesis.We also have that

coeff=-coeff

-coeff.

Altogether，this yields

deg≤deg-1=l+

and coeff ≥0 by the induction hypothesis.This concludes the induction.

Finally，we observe that the part of ∂q containing is given by q_d-1t₁+，which implies p=q_d-1t₁+∂q_dby p=∂q.If d is even，then we obtain that

coeff=coeff+

coeff，

which is different from zero by the properties shown above.Consequently，we have deg≥l+-1≥-1 so that p does not only contain monomials with i≤-2.If d is odd，then

deg=l+>l+≥deg

by the properties shown above，which implies that

deg=deg+1=l+≥

Hence，p does not only contain monomials with i≤.

Example 3.Compute the following integrals involving Ai:

∫Ai'(x)²dx and ∫(45x³-26)Ai(x)⁵dx.

Consider the differential ring(C[t₁，t₂，t₃]，∂) generated by Ai(x) with

∂t₁=1， ∂t₂=t₃ and ∂t₃=t₁t₂.

We apply the reduction rules in Theorem 3 to

f₁= and f₂=45-26

as follows:

f₁=　　　　　

=∂G_0，0，2-t₁

=∂

=∂

　and

f₂=-26

=∂+-90t₁t₃-26

=∂-26

=∂

=∂(-26t₁+45t₃+20-60t₁+24)

Moreover，the second integral cannot be computed by Mathematica 13.1.

In summary，we present two reduction systems for the differential ring generated by Airy functions due to different monomial orderings and prove that both of them are complete.Then for any polynomial in the above ring，we can determine whether it has an integral in the same ring，and if yes，we can compute such an integral by reduction.Furthermore，according to the complete reduction system in Theorem 3，any polynomial can be decomposed as a sum of a derivative of another one and a polynomial with minimal leading term，which cannot be reduced anymore.Together with the structure theorem given by Bronstein，we can determine the denominator as well as the logarithmic part of the integral so that we are able to determine the elementary integrability of an element in the differential filed further using a reduction system adapted to the denominator.Later，we will give a more formal way of reduction systems as well as rigorous weighted degree bounds for the integrals.

Conflict of interest:The authors declare no conflict of interest.

---

参考文献(References)

[1] Bostan A.;Chen S.;Chyzak F.;Li Z.;Xin G.Hermite Reduction and Creative Telescoping for Hyperexponential Functions.Proceedings of the International Symposi- um on Symbolic and Algebraic Computation,pages 77- 84,ACM Press,2013.
https://doi.org/10.48550/arXiv.1301.5038
[2] Bostan A.;Chyzak F.;Lairez P;Salvy B.Generalized Hermite Reduction,Creative Telescoping,and Definite Integration of D-Finite Functions.Proceedings of the International Symposium on Symbolic and Algebraic Computation,pages 95-102,ACM Press,2018.
https://doi.org/10.1145/ 3208976.3208992
[3] Bostan A.;Lairez P;Salvy B.Creative telescoping for rational functions using the Griffiths-Dwork method.Proceedings of the International Symposium on Symbolic and Algebraic Computation,pages 93-100,ACM Press,2013.
https://doi.org/10.1145/2465506.2465935
[4] Boettner S.T.Mixed Transcendental and Algebraic Extensions for the Risch-Norman Algorithm.PhD Thesis, Tulane Univ.,New Orleans,USA,2010.
[5] Bronstein M.Symbolic Integration I-Transcendental Functions.2nd ed.,Springer,2005.
https://doi.org/10.1007/b138171
[6] Bronstein M.pmint-The Poor Man’s Integrator.Version 1.1,2005.
http://www-sop.inria.fr/cafe/Manuel.Bronstein/pmint/
[7] Chen S.;Du H.;Li Z.Additive Decompositions in Primitive Extensions.Proceedings of the International Symposium on Symbolic and Algebraic Computation,pages 135-142,ACM Press,2018.
https://doi.org/10.1145/3208976.3208987
[8] Chen S.;Kauers M.;Koutschan C.Reduction-Based Creative Telescoping for Algebraic Functions.Proceedings of the International Symposium on Symbolic and Algebraic Computation, pages 175-182,ACM Press,2016.
https://doi.org/10.1145/ 2930889.2930901
[9] Chen S.;van Hoeij M.;Kauers M.;Koutschan C.Reduction- based creative telescoping for Fuchsian D-finite functions.Journal of Symbolic Computation 85,Pages 108-127,2018.
https://doi.org/10.1016/j.jsc.2017.07.005
[10] Davenport J.H.The Parallel Risch Algorithm(I). Proc.EUROCAM’82,pages 144- 157,1982.
https://dl.acm.org/doi/10.5555/ 646656.700248
[11] Olver F.W.J.;Olde Daalhuis A.B.;Lozier D.W.; Schneider B.I.;Boisvert R.F.;Clark C.W.;Miller B. R.;Saunders B.V.;Cohl H.S.;McClain M.A.(eds.) NIST Digital Library of Mathematical Functions.
https://dlmf.nist.gov/,Release 1.1.10 of 2023-6-15.
[12] Du H.;Guo J.;Li Z.;Wong E.An Additive Decomposition in Logarithmic Towers and Beyond.Proceedings of the International Symposium on Symbolic and Algebraic Computation,pages 146-153,ACM Press,2020.
https://doi.org/10.1145/ 3373207.3404025
[13] Davenport J.H.;Trager B.M.On the Parallel Risch Algorithm(II).ACM Trans.Mathematical Software 11,pages 356-362,1985.
https://doi.org/10.1145/6187.6189
[14] Geddes K.O.;Stefanus L.Y..On the Risch-Norman Integration Method and Its Implementation in MAPLE. Proceedings of the International Symposium on Symbolic and Algebraic Computation,pages 212-217, ACM Press,1989.
https://doi.org/10.1145/74540.74567
[15] Geddes K.O.;Czapor S.R.;Labahn G.Algorithms for Computer Algebra.Springer Science & Business Media,1992.
[16] van der Hoeven J.Constructing reductions for creative telescoping-The general differentially finite case.Applicable Algebra in Engineering,Communication and Computing 32,pages 575-602,2021.
https://doi.org/10.1007/s00200-020-00413-3
[17] Kovacic J.J.An Algorithm for Solving Second Order Linear Homogeneous Differential Equations.Journal of Symbolic Computation 2,pages 3-43,1986.
https://doi.org/10.1016/ S0747-7171(86)80010-4
[18] Norman A.C.A Critical-Pair/Completion based Integration Algorithm.Proceedings of the International Symposium on Symbolic and Algebraic Computation, pages 201-205,1990.
https://doi.org/10.1145/96877.96926
[19] Norman A.C.;Moore P.M.A.Implementing the new Risch Integration algorithm.Proc.4th International Colloquium on Advanced Computing Methods in Theoretical Physics,pages 99-110,1977.
[20] Raab C.G.Definite Integration in Differential Fields. PhD thesis,RISC-Linz,Johannes Kepler University, Linz,Austria,2012.
http://www.risc.jku.at/publications/download/risc_4583/PhD_CGR.pdf
[21] Ritt J.F.Integration in Finite Terms-Liouville’s Theory of Elementary Methods.Columbia University Press, New York,1948.
https://doi.org/ 10.1007/978-3-030-98767-1_3
[22] Risch R.H.The problem of integration in finite terms. Transactions of the American Mathematical Society 139,pages 167-189,1969.
[23] Risch R.H.The solution of integration in finite terms. Bulletin of the American Mathematical Society 76,pages 605-608,1970.
[24] Raab C.G.;Singer M.F.(eds.).Integration in Finite Terms:Fundamental Sources.Texts & Monographs in Symbolic Computation,Springer,2022.
https://doi.org/10.1007/978-3-030-98767-1
[25] Schneider C.;Blümlein J.(eds.).Computer algebra in quantum field theory:Integration,summation and special functions.Texts & Monographs in Symbolic Computation, Springer,Vienna,2013.
[26] Vallée O.;Soares M.Airy Functions and Applications to Physics.2nd ed.,Imperial College Press,2010.

Complete Reduction Systems for Airy Functions

Hao Du^1,2,*, Clemens G.Raab³

(1. School of Science, Beijing University of Posts and Telecommunications (BUPT) , Beijing 102206, China
2. Key Laboratory of Mathematics and Information Networks (BUPT) , Ministry of Education, Beijing 102206, China
3. Institute for Algebra, Johannes Kepler University Linz (JKU) , Linz 4040, Austria)

Abstract: The computation of indefinite integrals in certain kind of “closed form”,which is known as symbolic integration,is an important research subarea of computer algebra.After implementing the recursive Risch algorithm partly,it was realized that efficient algorithms can be achieved by a parallel approach.This led to the famous Risch-Norman algorithm.However,this approach relies on an ansatz with heuristic degree bounds.Norman’s completion-based approach provides an alternative for finding the numerator of the integral avoiding heuristic degree bounds.However,depending on the differential field and on the selected ordering of terms,it may happen that the completion process does not terminate and yields an infinite number of reduction rules.We apply Norman’s approach to the differential field generated by Airy functions,which play an important role in physics.By fixing adapted orderings and analyzing the process in the concrete case,we present two complete reduction systems for Airy functions by finitely many formulae to denote infinitely many reduction rules. 

Keywords: Symbolic integration, Risch-Norman algorithm, Infinite reduction systems

DOI: 10.48014/bcam.20230724002

Citation: Hao Du,Clemens Raab.Complete reduction systems for Airy functions[J].Bulletin of Chinese Applied Mathematics,2023,1(1):10-22.