

基于阿基米德螺线与碰撞检测的运动轨迹问题研究
(湖北理工学院, 黄石 435000)
摘要: 根据传统文化遗产板凳龙的运动展开研究, 板凳龙表演涉及复杂的螺旋运动轨迹和多节点的协同运动, 对其建模和优化提出了极高的要求。为了深入理解其运动特点并提高安全性及观赏性, 探索了阿基米德螺旋运动轨迹的建模、碰撞检测以及优化问题的解决方案。针对复杂运动系统中的建模与求解问题, 运用中心差分法、牛顿迭代法、二分搜索法和仿真模拟技术等方法; 部分选择性创新地提出碰撞检测方法以及将约束条件转换为优化问题的模型; 采用多阶段自适应优化算法, 进一步提高了系统性能; 研究螺旋运动轨迹的数学建模、碰撞检测模型的建立和运动系统的整体性能优化; 解决了运动系统中的多重建模与求解难题。该成果不仅提供了对板凳龙运动的精确描述, 还为天体轨道设计、DNA双螺旋结构、蛋白质折叠等复杂系统的研究提供了新的思路和解决方案, 为类似动态系统的运动优化和性能提升提供了新的思路与技术支持。
关键词: 阿基米德螺线, 碰撞检测, 路径优化, 运动系统设计
DOI: 10.48014/bcam.20240918001
引用格式: 吴迪, 毛智文, 钟畅. 基于阿基米德螺线与碰撞检测的运动轨迹问题研究[J]. 中国应用数学通报, 2024, 2(4): 12-18.
文章类型: 研究性论文
收稿日期: 2024-09-18
接收日期: 2024-10-23
出版日期: 2024-12-28
1 引言
起源于汉代的“板凳龙”作为龙文化传播的载体,已经被列为国家级非物质文化遗产推荐项目。该项目以其鲜明的地方特色和文化标识展现了浙闽地区悠久历史与丰富文化底蕴,表现了当地人民对龙文化的独特理解和深厚情感,感受到了传统文化在现代社会中的活力与价值,在社会方面发挥凝聚、向上作用[1,2]。
“板凳龙”用一块长341cm、宽30cm的木板作为龙头,龙身和龙尾每节板凳长220cm、宽30cm,所有板凳预留两个孔中心距离板头27.5cm且孔径为5.5cm的圆孔以供连接。将板凳逐一扎制并拼接,形成一条完整的总计具有223节的板凳龙。表演中,龙身和龙尾紧密配合龙头的动作,通过精准的步伐和默契的配合,呈现出流畅的圆盘状形态。
本研究围绕板凳龙的运动轨迹建模与优化展开,重点解决其在不同阶段的运动特点,如盘入、调头、盘出等复杂情境。为了详细刻画这些运动过程,首先基于阿基米德螺旋线对板凳龙的整体运动轨迹进行了数学建模,模拟了龙头、龙身及龙尾沿螺旋线运动时的路径和速度变化。该模型精确描述了龙头前把手的匀速运动,并推导出龙身和龙尾各节点的运动规律。
在此基础上,本研究还考虑了实际舞龙过程中可能出现的碰撞问题,采用了几何建模和碰撞检测算法,重点分析了板凳相互接触或发生碰撞的情境。通过将碰撞问题近似为两个旋转长方体的交叠,我们引入了碰撞检测算法,并结合二分搜索法精确定位了碰撞发生的时间和位置,确保在实际表演中能够避免碰撞的发生。此外,研究还对板凳龙的调头路径进行了优化。通过设计一段符合调头空间约束的S形曲线,将舞龙队的顺时针盘入转化为逆时针盘出。我们通过调整螺距和圆弧半径,确保龙头顺利完成调头的同时,缩短了调头路径,并避免各节点之间的碰撞。
阿基米德螺线是一种在自然界和人类设计中广泛存在的曲线[3]。通过对板凳龙运动轨迹的深入研究与探讨,对其他领域具有一定的应用前景,还能在现代科技应用中寻找到新的研究方向,从而推动文化与科技的双向发展。例如,其庞大而灵活的结构设计,为仿生机器人、柔性结构的研发提供了新的思路;同时,基于阿基米德螺线的运动模型分析,也可应用于其他领域,如航天器轨道设计、可控旋转运动的机械臂、精密传感器的路径规划等。
2 运动轨迹
设定当前龙头前把手的行进速度始终保持1m/s,螺距为55cm。
2.1 阿基米德螺线
设立极坐标系,以螺线等距螺线半径随极角线性增加,在极坐标系中的方程为:
r(θ)=a+bθ(1)
其中,r(θ)是螺线半径,θ是极角,参数a定义了螺旋线的起始半径,b决定了螺旋的增量。代入上述公式得到:
![]() =b(2)
=b(2)
而螺距p和螺旋线参数b的关系[4]:
b=![]() (3)
(3)
可以计算出参数b的值。
将螺距p=0.55m代入公式中,得到:
b=![]() ≈
≈![]() (4)
(4)
利用微分方程描述了角度θ随时间t的变化:
![]() =-
=-![]() (5)
(5)
阿基米德螺旋线弧长s(θ)的计算公式为:
s(θ)=![]() (6)
(6)
其中,sinh-1(θ) 是反双曲正弦函数[5],定义为:
sinh-1(θ)=ln![]() (7)
(7)
为了确定在某一时刻的龙头位置,需要得到龙头的角度,s(θ)是螺旋线弧长函数,starget是当前时刻龙头前把手经过的弧长,C是初始弧长,因此我们可以得到以下函数:
f![]() =s(θ)-
=s(θ)-![]() (8)
(8)
龙头的极径rhead:
rhead=b·θhead(9)
相邻把手位置约束方程:
![]() +
+![]() =d2(10)
=d2(10)
根据阿基米德螺旋线弧长公式综合上述两式,依赖于相邻节点位置和速度的目标函数对每一秒进行迭代计算龙头的极角θhead(t+1),将极坐标系转换成平面直角坐标系
![]() (11)
(11)
假设把手连接处不受摩擦力影响。又龙头和板凳之间的固定相连,故可逐步计算每个部分的位置,同理求解出龙身及龙尾的极角。
由于已经知道龙整体的位置且龙头速度恒定,利用中心差分法[6],并将在x轴与y轴方向上的速度合成,故节点的速度vi的计算公式为:
vi=![]() (12)
(12)
其中,Δt是两时间间隔,设置一个非常小的时间步长参数[7]。
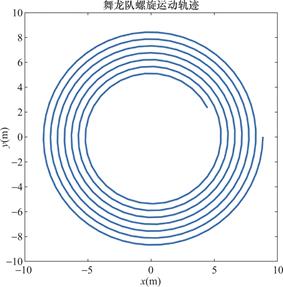
图1 舞龙队未掉头前轨迹
Fig.1 The trajectory of the dragon dance team before turning around
板凳龙的运动具有一定的周期性。各节点的相对位置和速度受龙头运动的影响,舞龙队速度趋近于1m/s。随着时间的推移,各坐标的变化幅度逐渐减小,这反映了舞龙队逐渐向螺线中心靠拢的过程。靠近龙头的部分速度变化较小;而靠近龙尾的部分速度变化较大。这反映了舞龙队不同部分受到的加速度不同由于板凳之间的连接和重叠,板凳龙的形状无法完全遵循螺线。
2.2 碰撞检测
当舞龙队从进入状态到出来状态时,需要合理化路径,确保不能发生碰撞。为了判断是否发生碰撞,可以使用它们的中心点坐标,以及在运动过程中发生的坐标变换[8]。
将每个板凳抽象成规则矩形,设定待检测的两板凳分别为长方形1和长方形2。
长方形边的斜率k:
k=![]() (13)
(13)
其中,(X1(1),X1(2))和(X2(1),X2(2))是板凳的前后把手的坐标。斜率k描述了两个长方形边的倾斜程度。
长方形中线的垂线斜率k':
k'=-![]() (14)
(14)
表示长方形的边垂直的直线的倾斜程度。
长方形的中心点Xi,center:
Xi,center=![]() (15)
(15)
其中i表示第i个长方形的标号。长方形的中心点是长方形的几何中心。
可以用矩阵A描述两个长方形中线垂直方向上的约束条件,定义为:
A=![]() (16)
(16)
这个矩阵的第一行和第二行分别表示两个长方形中线垂线的斜率。矩阵的列包含了每个长方形垂线的斜率和-1(表示y轴的偏移)。
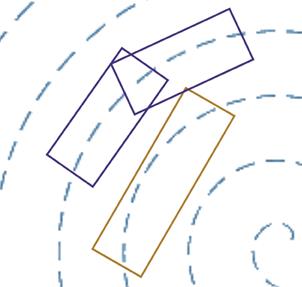
图2 碰撞轨迹
Fig.2 Collision trajectory
在板凳龙运动过程中,板凳的中心点随时间变化。假设板凳的中心点坐标为(xi![]() ,yi
,yi![]() )。设龙头的坐标为(xhead
)。设龙头的坐标为(xhead![]() ,yhead
,yhead![]() )。连接板凳上的两圆孔中心,两中线垂线的交点为新原点P。
)。连接板凳上的两圆孔中心,两中线垂线的交点为新原点P。
P=A-1·![]() (17)
(17)
把长方形1所有的离散点都按照新坐标旋转,若有点出现在长方形2区域,即为碰撞。将长方形1设置合适范围生成在坐标轴方向上均匀分布的n个离散点,这些点可以构成一个矩形区域。通过旋转矩阵T进行坐标旋转。使用旋转矩阵T将离散点坐标从第一个长方形的坐标系转换到第二个长方形的坐标系。该矩阵为旋转后的点集,用于检查点是否在第二个长方形的区域内。
T=![]() (18)
(18)
XYnew=T·![]() (19)
(19)
δθ为旋转角度。
检查所有旋转后x坐标值与第二个长方形长的差值的绝对值是否小于板凳宽的一半。这意味着点在长方形二的宽度范围内。如果旋转后的离散点中有位于第二个长方形的区域内的点,则该区域非空,表示两个长方形相交。
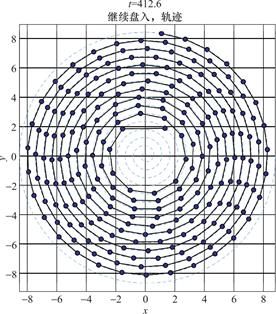
图3 一直盘入的终止时刻
Fig.3 Termination time of continuous disk loading
舞龙队不能继续行进的终止时刻,即板凳之间即将发生碰撞的临界状态[9]。利用坐标转换判断碰撞,接着,设计高效算法推进时间,并在每个时间步检查是否发生碰撞,可用二分法和逐步逼近法确定碰撞时刻并尽可能减少判定时间间隔。最终将终止时刻代入计算,得到关键节点的位置和速度。
3 综合动态路径规划与优化
舞龙队从进入状态到出来状态将由顺时针盘入调头切换为逆时针盘出,故需要一定的调头空间。设置调头空间是以螺线中心为圆心、直径为9m的圆形区域。
为了确定舞龙队的合理美观行驶路线,我们提出了一个创新的多阶段、多目标动态路径规划与优化模型。该模型将整个运动过程细分为三个关键阶段:盘入、调头、盘出。每个阶段都配备了专门的运动方程和约束条件,而整个流程则通过连续性条件实现平滑过渡。核心策略是将路径规划问题转化为一个受约束的非线性优化问题。通过参数化调头曲线,并优化这些参数来寻找最优解。此外,模型还引入了多种约束条件,以确保运动过程的连续性和流畅性。
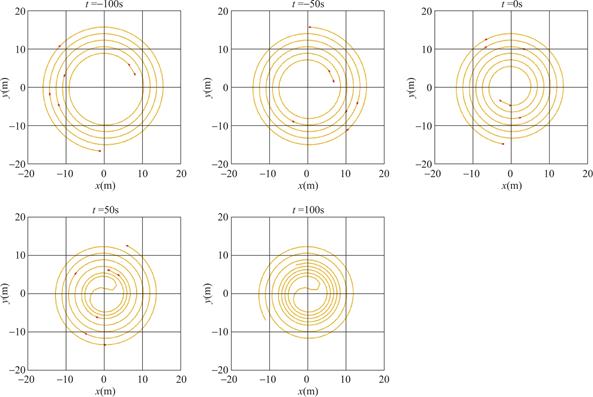
图4 不同阶段运行轨迹
Fig.4 Operating trajectories at different stages
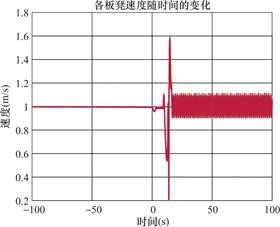
图5 板凳的v-t图像
Fig.5 V-T image of bench
3.1 约束条件
最小化调头曲线的总长度:
L=R1![]() +R2
+R2![]() (20)
(20)
调头空间边界约束,所有点需位于直径9m的圆内:
x2+y2≤![]() (21)
(21)
圆弧连接点位置连续性:
![]() (22)
(22)
切线方向连续性:
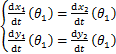 (23)
(23)
速度连续性约束:龙头前把手速度恒定为1m/s,需满足:
![]() +
+![]() =1
=1
螺线参数方程如下:
p=1.7m,r(θ)=aθ,x=aθcosθ,y=aθsinθ
其中,
a=![]() ≈0.2706m
≈0.2706m
3.2 多阶段动态优化
模型的关键组成部分包括螺线运动的几何特性,包括盘入和盘出的螺线参数方程;调头曲线的参数化表示,涉及圆弧的半径和圆心位置;运动的连续性约束,确保不同阶段之间的位置、速度和加速度的连续性;几何约束,例如调头空间的边界条件和螺线的切线条件;以及优化目标,即最小化调头曲线的总长度。
盘入螺线参数方程如下:
![]() (24)
(24)
盘入螺线参数方程如下:
![]() (25)
(25)
调头曲线由两个圆弧组成,半径分别为R1和R2,圆心坐标![]() 为和
为和![]() 。
。
第一段圆弧为:
![]() (26)
(26)
第二段圆弧为:
![]() (27)
(27)
为了实现这一模型,我们提出了一种自适应多阶段优化算法。该算法的核心理念是将整个优化过程分解为多个阶段,每个阶段专注于特定的子问题,并采用自适应策略动态调整优化参数和约束条件。算法的实施步骤包括初始化系统参数,例如螺距、板凳长度、把手间距等;设计多阶段优化流程,涵盖螺线衔接优化、调头曲线形状优化和全局微调;在各个阶段应用不同的优化策略和约束条件,逐步提高解决方案的质量;生成完整的运动轨迹,并进行结果验证与微调。
该算法的显著特点是其分阶段和自适应的特性。通过将优化过程分解为多个阶段,我们能够更有效地解决不同层次的问题。每个阶段都会根据当前的优化结果自动调整参数和策略,从而提高优化的效率。同时,算法在全局微调阶段确保了解决方案的全局最优性,实现了局部问题的有效处理与全局优化目标的和谐统一。
调头曲线与螺线相切,需满足位置和方向连续性。位置连续性:
![]() (28)
(28)
方向连续性:
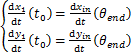 (29)
(29)
为了优化调头路径,通过调整圆弧半径、考虑曲率变化,通过遗传算法进行迭代,优化舞龙队的运动轨迹。我们需要给出逼近的方法:掉头区域的直径为9m,表示S形曲线中两个半圆的直径之和最大为9m。我们从这个最大的直径开始,将S形曲线的两端沿两个等距螺线不断减少,同时利用问题二的碰撞检测模型对其进行检测。当其发生碰撞时,就意味着逼近了最短的掉头曲线。
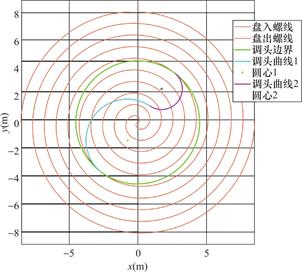
图6 掉头轨迹
Fig.6 U-turn trajectory
4 总结
本文以板凳龙为基础,在特定情形下,研究阿基米德螺线并且做出拓展。为了防止碰撞,模型利用矩阵变换和坐标旋转检测板凳之间的相对位置关系,判定是否相交。优化算法分阶段执行,逐步解决路径规划中的子问题,动态调整参数,确保全局最优解决方案。优化路径方面提出了一种创新的舞龙队行驶路径规划与优化模型,旨在确保路线的合理、美观和避免碰撞。该模型将运动分为三个阶段:盘入、调头、盘出,并通过螺旋线和圆弧的参数化方程、几何约束及运动连续性条件进行非线性优化,确保不同阶段平滑衔接。
利益冲突: 作者声明没有利益冲突。
[①] *通讯作者 Corresponding author:吴迪,18971955169@163.com
收稿日期:2024-09-18; 录用日期:2024-10-23; 发表日期:2024-12-28
参考文献(References)
[1] 周晨. 江西板凳龙研究[D]. 南昌: 江西师范大学, 2020. 2506+2514.
https://doi.org/10.3969/j.issn.1004-132X.2018.20.017
[2] 韦华丽. 北泉板凳龙文化的现状与传承[D]. 重庆: 西南大学, 2012.
https://doi.org/10.7666/d.y2086714.
[3] 凌云龙, 汪川, 张海潮. 基于阿基米德螺线的三导线环形磁导引[J]. 物理学报, 2020, 69(10): 101-109.
https://doi.org/10.7498/aps.69.20200284.
[4] 张瑞坤, 汪国昭. 阿基米德螺线的拟Bernstein基表示[J]. 计算机辅助设计与图形学学报, 2006, 18(7): 918-923.
https://doi.org/10.3321/j.issn:1003-9775.2006.07.004.
[5] 张士勤, 郭白妮. 反双曲正弦函数的单调性和不等式[J]. 数学季刊(英文版), 2009, 24(3): 384-388.
https://doi.org/10.3969/j.issn.1002-0462.2009.03.011.
[6] 郭双冰, 张志跃. 一类非线性发展方程的特征中心差分法[J]. 计算物理, 2007, 24(6): 637-646.
https://doi.org/10.3969/j.issn.1001-246X.2007.06.002.
[7] 周杰梁, 郑百林. 基于中心差分法的纤维结构碰撞动力学分析[J]. 力学季刊, 2011, 32(3): 466-472.
[8] 程启明, 赖宇生, 李剑辉, 等. 基于双dq坐标变换的模块化多电平矩阵变换器无源控制策略[J]. 电力自动化设 备, 2023, 43(4): 16-22.
https://doi.org/10.16081/j.epae.202206026.
[9] 杨海芬, 张辉, 蒋贤皓, 等. 基于拥堵预测的路径规划算法研究[J]. 电子科技大学学报, 2024, 53(3): 376-381.
https://doi.org/10.12178/1001-0548.2022333.
Study on Motion Trajectory Problem Based on Archimedean Spiral and Collision Detection
(Hubei Polytechnic University, HBPU, Huangshi 435000, China)
Abstract: This study investigates the motion characteristics of the traditional cultural heritage “Bandenglong” ( Bench Dragon) , a performance involving intricate spiral trajectories and coordinated multi-node movements, which demands high precision in modeling and optimization. To enhance safety, aesthetic performance, and operational efficiency, we propose a comprehensive framework integrating Archimedean spiral trajectory modeling, collision detection algorithms, and multi-stage dynamic path optimization. By employing numerical methods such as the central difference scheme, Newton-Raphson iteration, and binary search, alongside simulation techniques, we innovatively transform. collision constraints into optimization problems and develop a selective collision detection approach. A multi-phase adaptive optimization algorithm is introduced to dynamically adjust parameters, ensuring global optimality while addressing subproblems like spiral transition smoothing and collision avoidance. The established mathematical model accurately describes the spiral motion of the dragon’s head, body, and tail, resolving multi-scale modeling challenges in complex dynamic systems. Beyond its application to the Bandenglong, this framework offers novel insights and methodological support for diverse fields, including celestial orbital design, DNA double-helix structural analysis, and robotic path planning, thereby bridging cultural heritage preservation with modern technological advancements.
Keywords: Archimedean spiral, collision detection, path optimization, motion system design
DOI: 10.48014/bcam.20240918001
Citation: WU Di, MAO Zhiwen, ZHONG Chang. Study on motion trajectory problem based on archimedean spiral and collision detection[J]. Bulletin of Chinese Applied Mathematics, 2024, 2(4): 12-18.