

一类特定作用核的热力学Cucker-Smale模型的渐近稳定性
(北京化工大学, 北京 100029)
摘要: 聚集行为是常见的自然现象。动物的迁徙、细菌的运动以及心脏和脉搏的跳动都表现出一定的聚集行为。2007年, Cucker和Smale提出了可有效地刻画聚集行为的Cucker-Smale模型。2017年, Ha等人考虑了温度效应对聚集现象的影响, 对Cucker-Smale模型进行了改进。改进后的模型一般称为热力学Cucker-Smale模型 (简称TCS模型) 。具体而言: 本文探讨了一类特定作用核的热力学Cucker-Smale模型的渐近稳定性。当TCS模型的两个作用核函数ϕ (r) 和ζ (r) 均有界且存在严格大于0的下界时, 我们得到了TCS模型Cauchy问题的解会在一类特定初值下, 呈现指数稳定性的一个充分条件。特别的, 与以往的研究通常会假设ϕ (r) 和ζ (r) 有界且单调递减不同, 本文中我们对ϕ (r) 和ζ (r) 的单调性不做要求。此外, 我们还利用Matlab程序对本文结论的一维情形进行数值模拟。模拟结果显示, 在一组符合结论条件的初值下, 粒子的速度和温度会趋于同步, 而且它们的间距也保持有界, 从而进一步地验证了结论的正确性。
关键词: 热力学Cucker-Smale模型, 柯西问题, 渐近稳定性, 数值模拟
DOI: 10.48014/bcam.20241021001
引用格式: 闫盛伦, 孙俊彦, 毛智宇, 等. 一类特定作用核的热力学Cucker-Smale模型的渐近稳定性[J]. 中国应用数学通报, 2024, 2(4): 19-28.
文章类型: 研究性论文
收稿日期: 2024-10-21
接收日期: 2024-11-15
出版日期: 2024-12-28
1 引言
聚集行为是常见的自然现象。动物的迁徙、细菌的运动以及心脏和脉搏的跳动都表现出一定的聚集行为。聚集行为通常具有一定的目的性,例如,在生态学领域,聚集行为可促进种群繁殖、逃避天敌以及减少个体间的竞争,最终增强种群整体的安全系数。因此,对聚集行为的研究具有理论与应用意义。
1995年,匈牙利生物物理学家T.Vicsek等[1]首次利用数值实验的方法描述了群体运动的形成机理,并建立了Vicsek模型。A.Jadbabaie等[2]基于一定的假设条件下从数学的角度严格证明了上述数值实验的正确性。自T.Vicsek等人的工作后,出现了大量的数学模型来研究群体行为。2007年,Cucker教授和Smale教授上发表了可用来刻画聚集现象的Cucker-Smale模型[3]。对于一个由n个粒子组成的系统,设xi,vi分别代表第i个粒子的位置和速度,这里i=1,2,…,n。同时设粒子之间的作用核函数ω:R→R。在此符号系统下,Cucker-Smale模型的具体形式如下所示:
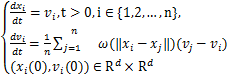 (1)
(1)
他们的研究表明,对于Cucker-Smale模型的作用核ω(r)=![]() ,当β≤1时,无论t=0时系 统的初始值取何值,Cucker-Smale的解都具有渐近稳定性,而当β>1时,只有当初始位置与速度均满足一定条件时,解才具有渐近稳定性。Cucker-Smale模型因其考虑到了系统中的全局相互作用,且在数学处理上有着其独特的优势,即解的大时间行为仅取决于初始值与作用核ω(r)。Cucker-Smale模型提出以来,许多研究者结合现实应用场景,选取不同的作用核ω(r),对其进行了深入的研究。例如,在文献[4]中,作用核ω(r)被取为ω(r)=
,当β≤1时,无论t=0时系 统的初始值取何值,Cucker-Smale的解都具有渐近稳定性,而当β>1时,只有当初始位置与速度均满足一定条件时,解才具有渐近稳定性。Cucker-Smale模型因其考虑到了系统中的全局相互作用,且在数学处理上有着其独特的优势,即解的大时间行为仅取决于初始值与作用核ω(r)。Cucker-Smale模型提出以来,许多研究者结合现实应用场景,选取不同的作用核ω(r),对其进行了深入的研究。例如,在文献[4]中,作用核ω(r)被取为ω(r)=![]() (称为奇异核)并对其一维情形下粒子的排序问题进行了详细的研究。当粒子数量n→¥时,Cucker-Smale模型的流体动力学极限形式亦广受关注,例如,文献[5]便对流体动力学Cucker-Smale模型的若干性质进行了研究。
(称为奇异核)并对其一维情形下粒子的排序问题进行了详细的研究。当粒子数量n→¥时,Cucker-Smale模型的流体动力学极限形式亦广受关注,例如,文献[5]便对流体动力学Cucker-Smale模型的若干性质进行了研究。
然而,Cucker-Smale模型具有其自身的局限性。Cucker-Smale模型仅考虑了相对速度、受力以及位置等内生变量对群体运动状态的影响,但还有大量聚集行为受到光照、温度等外生变量的影响。例如,文献[6]和文献[7]指出,蓝细菌是一种能够感知并响应光照强度及其方向变化的光合微生物,在一定条件下,这些细菌会主动地向光源运动。在文献[8]中,Ha等人考虑到了温度对聚集行为的影响,并基于Cucker-Smale系统建立了热力学Cucker-Smale模型(简称TCS模型)。
热力学Cucker-Smale模型是一种重要的刻画受热力学效应影响的聚集效应的常微分方程模型。对于一个由n个粒子组成的系统,设Ti代表第i个粒子的温度,其中i=1,2,…,n。同时设粒子之间的作用函数ϕ,ζ:R→R。在此符号系统下,TCS模型的具体形式如下所示:
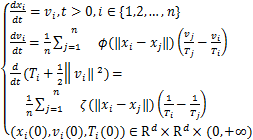 (2)
(2)
方程组(2)中其他项含义与(1)相同。
文献[8]的结论表明,当粒子的作用核为常 数且温度的数值远大于速度的范数,也就是将![]() 修正为
修正为![]() 时,TCS模型的解在小扰动条件下仍具有渐近稳定性。文献[9]考察了带有势场U=
时,TCS模型的解在小扰动条件下仍具有渐近稳定性。文献[9]考察了带有势场U=![]() 的TCS模型,该模型即在原始TCS模型的基础上将
的TCS模型,该模型即在原始TCS模型的基础上将![]() 修正为
修正为![]() +ÑU,文献[9]的作者基于文献[8]的结果,验证了当作用核满足单调递减且Lipschitz连续的条件时,模型的解具有渐近稳定性。文献[10]分别考察了整体有向图上的TCS模型的连续与离散形式,并提出了其柯西问题的渐近稳定性的一个充分条件。文献[11]考察了作用核为符 号函数时,TCS模型的解中的速度项将在有限时间 内取到相同的值。文献[12]考察了奇异作用核下TCS模型的渐近稳定性。与此类似,当粒子数n→¥时,借鉴统计力学思想的动理学TCS模型也广受关注,例如,文献[13]与文献[14]分别考察了动理学TCS模型分别与不可压缩和可压缩粘性流体力学方程组的耦合形式。
+ÑU,文献[9]的作者基于文献[8]的结果,验证了当作用核满足单调递减且Lipschitz连续的条件时,模型的解具有渐近稳定性。文献[10]分别考察了整体有向图上的TCS模型的连续与离散形式,并提出了其柯西问题的渐近稳定性的一个充分条件。文献[11]考察了作用核为符 号函数时,TCS模型的解中的速度项将在有限时间 内取到相同的值。文献[12]考察了奇异作用核下TCS模型的渐近稳定性。与此类似,当粒子数n→¥时,借鉴统计力学思想的动理学TCS模型也广受关注,例如,文献[13]与文献[14]分别考察了动理学TCS模型分别与不可压缩和可压缩粘性流体力学方程组的耦合形式。
在叙述本文结论前,我们给出TCS模型渐近稳 定性的数学定义。
定义1(TCS模型的渐近稳定性) 如果TCS模型(2)的解(xi,vi,Ti),i=1,2,…,n满足如下条件。
![]() ‖vi(t)-vj(t)‖=0,i,j=1,2,…,n
‖vi(t)-vj(t)‖=0,i,j=1,2,…,n
![]() |Ti(t)-Tj(t)|=0,i,j=1,2,…,n
|Ti(t)-Tj(t)|=0,i,j=1,2,…,n
![]() ‖xi(t)-xj(t)‖<+¥,i,j=1,2,…,n
‖xi(t)-xj(t)‖<+¥,i,j=1,2,…,n
则称此时TCS模型具有渐近稳定性。
值得注意的是,根据以上定义,TCS模型的渐近稳定性只意味着粒子之间的相对速度大小‖vi(t)-vj(t)‖与相对温度大小|Ti(t)-Tj(t)|随时间增加收敛至0,但这并不意味着vi(t)与Ti(t)本身收敛至定值。同时,粒子间距‖xi(t)-xj(t)‖作为时间的函数保持有界,也不意味着在任意时刻粒子的位置xi(t)在某一确定的有界区域内。
为便于叙述,本文主要符号说明如下:
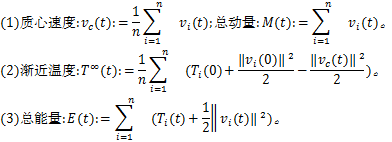
(4)相对速度:![]() (t):=vi(t)-vc(t);相对温度:
(t):=vi(t)-vc(t);相对温度:![]() (t)=Ti(t)-
(t)=Ti(t)-![]() (t)。
(t)。
注意到当TCS模型中的各个粒子的温度相等 且为定值时,即为Cucker-Smale模型。本文主要结论为如下定理:
定理1.1 如果TCS模型的作用核数ϕ(r)和ζ(r)满足如下条件:
(1)当r∈[0,+¥)时,ϕ(r),ζ(r)是Lipschitz连续函数。
(2)∀r∈[0,+¥),存在m1,m2,M1,M2∈(0,+¥)使得0<m1≤ϕ(r)≤M1,0<m2≤ζ(r)≤M2。
并且存在ε0>0使得各项初始值满足:
(1)![]()
(2)温度初值正则性:
![]()
(ii)![]() Ti(0)>0,
Ti(0)>0,![]() (0)>ε0
(0)>ε0
(iii)m1![]() >
>![]()
(iv)![]() >
>![]() +
+![]()
(i)~(iv)中的常数A1,A2,A3的定义是:
A1:=2m1![]() -
-![]()
A2:=![]() -
-![]() -
-![]()
A3:=![]() +
+![]()
那么,对于任意t∈[0,+¥),如下结论成立:
(1)速度的l2估计:
![]()
(2)温度的l2估计:
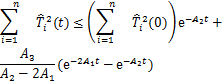
(3)间距有界性:
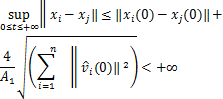
从而不难看出此时TCS模型具有渐近稳定性。
与以往结果相比,该定理的一个重要的创新点为不再对作用核函数的单调性作出要求,而是只需 要保证有严格正的下界。为证明TCS模型渐近稳定性,常见做法是根据作用核和初值的条件,对方程右端项进行代数放缩处理,构造耗散结构。因此,作用核函数不具备单调性的性质对提出新的耗散结构带来了挑战。本文中我们克服了这一挑战,证明了在此类作用核下,当初值满足一定条件时,TCS模型柯西问题的解同样具有渐近稳定性。
本文结构安排如下:在第二章中,我们提出并证明了TCS模型的动量守恒和能量守恒性质,并利用这些性质得到了TCS模型在此类作用核下的速度与温度的耗散结构。然而,此时得到的耗散结构只是局部成立,因此在第三章对定理1.1的证明中,我们首先利用常见的bootstrapping技巧将这一局部成立的耗散结构推广至整体,最后利用Gronwall不等式得到了速度和温度的渐近估计,并利用速度的渐近估计证明了粒子间距的有界性,得到了最终结论。在第四章,我们针对一维情形进行数值模拟,对结论进行进一步的佐证。
2 热力学Cucker-Smale模型的基本性质
在这一章节中,我们首先将利用热力学Cucker-Smale模型的对称性,从数学上证明TCS模型的能 量守恒与动量守恒性质。并利用该性质进行一系列代数放缩,得到其在定理1.1的初值条件下的耗散结构。本章节的结论在证明定理1.1的过程中至关重要。
引理2.1(守恒律) 令![]() 为TCS模型(2)的一个解,并且初始值满足‖M(0)‖<+¥与E(0)<+¥,i=1,2,…,n,则对于∀t∈[0,+¥),我们有动量守恒M(t)=M(0)与能量守恒E(t)=E(0)。
为TCS模型(2)的一个解,并且初始值满足‖M(0)‖<+¥与E(0)<+¥,i=1,2,…,n,则对于∀t∈[0,+¥),我们有动量守恒M(t)=M(0)与能量守恒E(t)=E(0)。
证明:首先证明动量守恒M(t)=M(0)。交换指标i与j并利用对称性ϕ(‖xi-xj‖)=ϕ(‖xj-xi‖)可得:
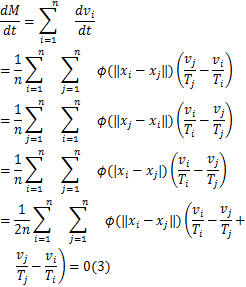
这就可证明TCS系统(2)动量守恒,即M(t)=M(0)。同理可证系统能量守恒E(t)=E(0)。根据该引理可立即得:vc(t)=vc(0)与![]() (t)=
(t)=![]() (0)。
(0)。
标注2.1 若vc(t)=0并记![]() =
=![]() (0),那么TCS系统(2)。等价于以下形式:
(0),那么TCS系统(2)。等价于以下形式:
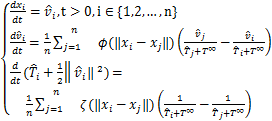
引理2.2(耗散结构) 令![]() 为TCS模型(2)的一个解,则当初值满足定理1.1的条件时,存在s∈(0,+¥],使得在区间[0,s)内有
为TCS模型(2)的一个解,则当初值满足定理1.1的条件时,存在s∈(0,+¥],使得在区间[0,s)内有
![]()
并且在区间[0,s)内如下微分不等式成立
(1)速度微分不等式:
![]() (4)
(4)
(2)温度微分不等式:
![]() (5)
(5)
证明:因为初始值满足
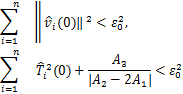
由解的连续性可知,只要s是一个充分小的正数,在区间[0,s)内便有
![]()
接下来,我们首先对速度进行估计:
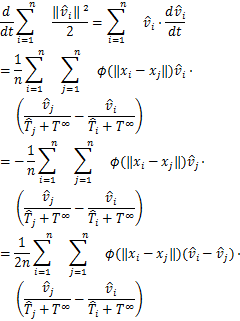
利用关系
![]() -
-![]()
=![]() (
(![]() -
-![]() )
)
+![]() (
(![]() -
-![]() )(6)
)(6)
可得
![]()
其中
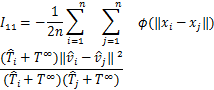
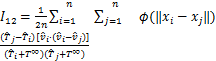 (7)
(7)
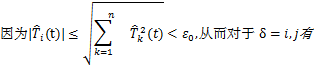
(x1(0),x2(0),x3(0),x4(0),x5(0))=(0.7094,2.1088,4.5787,3.9610,4.7975)
(v1(0),v2(0),v3(0),v4(0),v5(0))=(0.0696,0.0573,-0.0637,-0.0567,-0.0065)
(T1(0),T2(0),T3(0),T4(0),T5(0))=(10.0031,10.0154,9.9908,10.0320,10.0218)
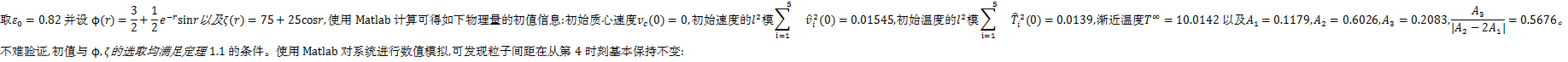
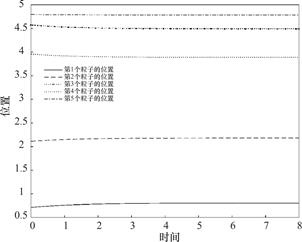
图1 位置模拟
Fig.1 Simulation of position
系统速度的渐近效应在第7.7时刻左右明显:
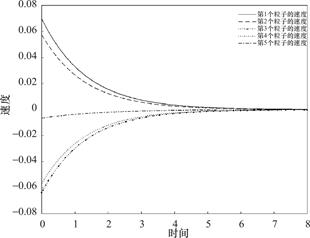
图2 速度模拟
Fig.2 Simulation of velocity
系统温度的渐近效应在第1.8时刻左右明显:
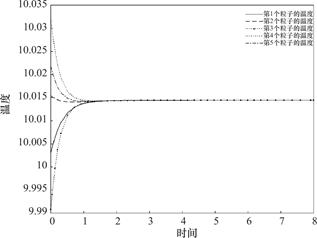
图3 温度模拟
Fig.3 Simulation of temperature
利益冲突: 作者声明没有利益冲突。
[②] *通讯作者 Corresponding author:邹委员,zwy@amss.ac.cn
收稿日期:2024-10-21; 录用日期:2024-11-15; 发表日期:2024-12-28
参考文献(References)
[1] T. Vicsek, A. Czirok, E. Ben-Jacob, et al. Novel type of phase transition in a system of self-driven particles[J]. Physical Review Letters, 1995, 5(6): 1226-1229.
https://doi.org/10.1103/PhysRevLett.75.1226.
[2] A. Jadbabaie, J. Lin, A. S. Morse. Coordination of groups of mobile autonomous agents using nearest neighbor rules[J]. IEEE Transactions on Automatic Control, 2003, 48(6): 988-1001.
https://doi.org/10.1109/tac.2003.812781.
[3] F. Cucker, S. Smale. Emergent behavior in flocks[J]. IEEE Transactions on Automatic Control, 2007, 52(5): 852-862.
https://doi.org/10.1109/TAC.2007.89584.
[4] X. T. Zhang, T. T. Zhu. Complete classification of the asymptotical behavior for singular C-S model on the real line[J]. Journal of Differential Equations, 2020, 269(1): 201-256.
https://doi.org/10.1016/j.jde.2019.12.004
[5] R. Shu and E. Tadmor. Flocking hydrodynamics with external potentials[J]. Arch. Ration. Mech. Anal. , 238(2020): 347-381.
https://doi.org/10.1007/s00205-020-01544-0
[6] D. Bhaya. Light matters: phototaxis and signal transduction in unicellular cyanobacteria[J]. Molecular Microbiology, 2004, 53(3): 745-754.
https://doi.org/10.1111/j.1365-2958.2004.04160.x
[7] D. Bhaya, K. Nakasugi, F. Fazeli, et al. Phototaxis and impaired motility in adenylyl cyclase and cyclase receptor protein mutants of synechocystis sp. strain PCC 6803[J]. Journal of Bacteriology, 2006, 188(20): 7306-7310.
https://doi.org/10.1128/JB.00573-06a
[8] S. Y. Ha, T. Ruggeri. Emergent dynamics of a thermodynamically consistent particle model[J]. Archive for Rational Mechanics and Analysis, 2017, 223(3): 1397-1425.
https://doi.org/10.1007/s00205-016-1062-3
[9] H. J. Cho, L. L. Du, S. Y. Ha. Emergence of a periodically rotating one-point cluster in a thermodynamic Cucker- Smale ensemble[J]. Quarterly of Applied Mathematics, 2022, 80(1): 1-22.
https://doi.org/10.1090/qam/1602
[10] J. G. Dong, S. Y. Ha, D. Kim, Emergent behaviors of continuous and discrete thermomechanical Cucker- Smale models on general digraphs[J]. Mathematical Methods in the Applied Sciences, 29(2019), 589-632.
https://doi.org/0.1142/S0218202519400013
[11] H. Ahn, S. Noh. Finite-in-time flocking of the thermodynamic Cucker-Smale model[J]. Networks and Heterogeneous Media, 2024, 19(2): 526-546.
https://doi.org/10.3934/nhm.20240233
[12] H. Ahn. Uniform stability of the Cucker-Smale and thermodynamic Cucker-Smale ensembles with singular kernels[J]. Networks and Heterogeneous Media, 2022, 17(5): 753-782.
https://doi.org/10.3934/nhm.2022025
[13] Y. P. Choi, S. Y. Ha, J. Jung, et al. Global dynamics of the thermomechanical Cucker-Smale ensemble immersed in incompressible viscous fluids[J]. Nonlinearity, 2019, 32(5): 1597-1640.
https://doi.org/10.1088/1361-6544/aafaae
[14] Y. P. Choi, S. Y. Ha, J. Jung, et al. On the coupling of kinetic thermomechanical Cucker-Smale equation and compressible viscous fluid system[J]. Journal of Mathematical Fluid Mechanics, 2020, 22(4).
https://doi.org/10.1007/s00021-019-0466-x
A Symptotic Stability of Thermodynamic Cucker-Smale Model with a Specific Interacting Kerne
(Beijing University of Chemical Technology (BUCT) , Beijing 100029, China)
Abstract: Gathering behavior. are commonly observed in nature. Animal migration, bacterial movement, and the beating of the heart and pulse, exhibit collective behaviors all exhibit certain aggregation behaviors. In 2007, Cucker and Smale proposed the Cucker-Smale model, which can effectively characterize aggregation behavior. In 2017, Ha et al improved the Cucker-Smale model, which considered the effect of temperature on aggregation phenomena. This improved model is generally referred to as the thermodynamic Cucker- Smale model (TCS model for short) . Specifically, this article explores the asymptotic stability of thermodynamic Cucker-Smale model with a specific interacting kernel. When the two action functions ϕ (r) and ζ (r) of the TCS model are both bounded and have a lower bound which is strictly greater than 0, we obtain a sufficient condition for the exponential stability of the solution to the Cauchy problem of the TCS model. Specifically, previous studies have typically assumed that ϕ (r) and ζ (r) are bounded and monotonically decreasing, but in this article, we do not require monotonicity for ϕ (r) and ζ (r) . In addition, we also used Matlab programs to numerically simulate the one-dimensional case of the conclusions presented in this paper. The simulation results show that under a set of initial values that meet the conclusion conditions, the velocity and temperature of particles tend to synchronize, and their spacing remains bounded, further verifying the correctness of the conclusion.
Keywords: Thermodynamical Cucker-Smale Model, cauchy problem, asymptotic stability, numerical simulation
DOI: 10.48014/bcam.20241021001
Citation: YAN Shenglun, SUN Junyan, MAO Zhiyu, et al. A symptotic stability of thermodynamic Cucker- Smale model with a specific interacting kernel [J]. Bulletin of Chinese Applied Mathematics, 2024, 2(4): 19-28.