板凳龙行径位置计算的动态反馈算法
(1. 陕西师范大学数学与统计学院, 西安 710119
2. 陕西师范大学物理学与信息技术学院, 西安 710119)
摘要: 本文探讨了板凳龙沿阿基米德螺线盘入过程中, 各把手位置的确定方法。首先, 根据各把手盘入的行径特征, 确定对应极角的定量搜索范围, 为后续算法提供初值。随后, 提出了一种用于计算后一把手位置的动态反馈算法, 该算法有效避免了在求解非线性方程组时出现的多解问题。此外, 为提高计算效率, 研究了不同极角与迭代参数的函数设计。在仿真环境下, 验证了该动态反馈算法的有效性。
DOI: 10.48014/bcam.20241118001
引用格式: 郑雯欢, 郑姝艺, 陈森, 等. 板凳龙行径位置计算的动态反馈算法[J]. 中国应用数学通报, 2025, 3(1): 1-9.
文章类型: 研究性论文
收稿日期: 2024-11-18
接收日期: 2024-12-15
出版日期: 2025-03-28
1 Introduction
As an intangible cultural heritage of China，the bench dragon can be traced back to the Song Dynasty.It has passed through the Song，Yuan，Ming，Qing，and Republic of China for more than a thousand years[1].Among the bench dragon folklore in many places，the most famous is the Youlong bench Dragon in Huizhou[2].Youlong bench dragon is one of the most characteristic traditional folk activities of Yulong Village in Huizhou.On the fifteenth day of the first lunar month every year，villagers organize the bench dragon event to express their hope for a better life in the coming year.The bench dragon consists of a dragon head bench and several dragon body benches，which are connected by handles.The villagers use handles to drive the dragon forward.As the dragon advances，the dragon body benches are circling in the shape of a spiral.The bench dragon travels fast and can turn around while traveling.In the marching process，the speed of movement changes rapidly，the distance between the benches is small，and there can be no collisions[3].Successful performance of the bench dragon requires a high degree of tacit understanding among the performers.The activities of bench dragon mainly contain two parts:coiling the dragon body and turning the dragon over.After more than a thousand years of inheritance and development，the bench dragon has become a vivid depiction of national cohesion[4].It is not only a treasure of Chinese intangible cultural heritage，but also a vivid embodiment of the spirit of unity and the common endeavor of the Chinese nation[5].
The Problem A of 2024 Contemporary Undergraduate Mathematical Contest in Modeling sets up a series of problems based on the performance of bench dragon.The problem focuses on solving the position of each part of bench dragon during the performance，including dragon head and dragon body.It is crucial to determine the position of the latter handle based on the position of the former handle，involving the solution of nonlinear equations[6,7].Due to the nonlinearity，it is hard to explicitly solve the nonlinear equations.Although there are numerous numerical methods for solving nonlinear equations[8,9]，the focused method to solve the position of each handle of bench dragon has not been fully studied.
The paper investigates the focused method to calculate the moving position of bench dragon.Based on the idea of feedback[10-12]，the paper proposes a dynamical feedback algorithm for iteratively solving the latter handle position by the information of the former one[13,14].The main contributions of the paper are shown as follows.
1)The searching range of the polar angle of the latter handle is quantitatively established，leading to a quantitative selection of the initial value in iterative feedback algorithm.
2)A dynamical feedback algorithm for iteratively solving the latter handle position is proposed.Furthermore，a functional design of iterative parameter based on the polar angle is proposed，which promotes the computational efficiency.
The rest of the paper is organized as follows.In Section 2，the problem formulation is presented.In Section 3，the quantitative searching range of the polar angle and the design of the dynamical feedback algorithm are given.In Section 4，the simulation results with constant iterative parameters are given.In Section 5，the algorithm is further improved to the iterative parameter as a variable.
2 Problem Description
Consider a bench dragon consisting of 
sections of benches.The first section is the dragon head，the next 
sections are the dragon body，and the last section is the dragon tail.The schematic diagram of bench dragon is shown in Fig.1.
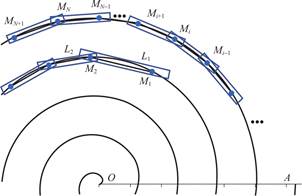
Fig.1 Bench dragon schematic diagram
Two neighboring benches are connected by a handle.Each handle point is denoted as 
，
.The former handle of the dragon head is denoted by 
.The distance between the former and latter handle of the dragon head is 
，and the distance between the rest neighboring handles are 
.The bench dragon coils clockwise along an equidistant spiral of pitch 
.The center of each handle is located on the spiral.The former handle of the dragon head has a constant traveling speed 
.At the initial time，the former handle of the dragon head is located at the point 
of the 
-th turn of the spiral.Moreover，the rest of the benches are aligned along a trajectory extending outward from the spiral at the initial time.
Denote the center of the spiral as the pole 
and the ray 
as the polar axis to establish a polar coordinate system.The positive direction of the angle is clockwise.The polar equation of the 
-th handle in the coiling process of the bench dragon satisfies the following equation:
(1)
where ，
is the polar radius of the -th handle at the time 
，
is the polar radius of the -th handle at the initial moment，
is the polar angle of the -th handle at the time ，and is the pitch.
To determine the position of each handle of the bench dragon during the traveling process，it is necessary to calculate the latter handle position based on the former handle position.However，the general algorithms for solving nonlinear equations have a high computational time complexity，and it is difficult to ensure the accuracy due to the multiplicity of solutions[15].To promote the computational efficiency and avoid the multi-solution problem，the paper proposes an algorithm based on feedback to calculate the position of handles.
3 Dynamical Feedback Algorithm
3.1 The former handle of the dragon head
This subsection establishes the function from the time to the polar angle of the former handle of dragon head.
The path of the former handle of the dragon head along the spiral coil is an arc.The relation between the arc length 
and the polar angle 
can be obtained as follows:
(2)
By substituting(1)into(2)，the relation between the arc length of the former handle of the dragon head and the polar angle can be obtained as follows:
(3)
The former handle of the dragon head moves with the velocity ，leading to 
.Based on the equation(3)，the relation between the polar angle of the former handle of the dragon head and time can be established:
(4)
The polar angle of the former handle of the dragon head with respect to can be obtained by solving(4).Based on the solution of(4)and the transform between Cartesian coordinates and polar coordinates，the coordinate of in the Cartesian coordinate system can be determined:
(5)
where 
is the abscissa of the -th handle in the Cartesian coordinate system，and 
is the ordinate of the -th handle in the Cartesian coordinate system.
3.2 Dynamical feedback algorithm
3.2.1 Searching range of polar angle
Before the detailed design of dynamical feedback algorithm，the initial value of iterative algorithm is discussed in this subsection.
Firstly，the possible searching range of the polar angle of the latter handle is analyzed.To concisely introduce the calculation，the -th handle is taken as an example，and the searching range of the polar angle of based on the coordinates of is given in the following steps.The schematic of positional relations between and 
is given in Fig.2.
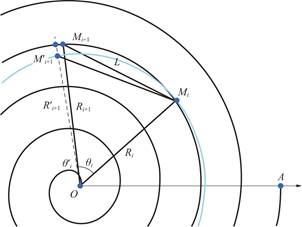
Fig.2 The searching range of the angle of the latter handle
Step 1:Due to the polar radius of the -th handle，namely 
，a circle 
with the radius and the center can be constructed.Construct a circle 
with the -th handle point as the center and the chord length 
as the radius，where satisfies the following relations:
(6)
Step 2:The point of intersection of circle and circle is denoted as 
.By comparing the position of and ，it can be obtained that:
(7)
where 
is the polar radius corresponding to ，
is the included angle between the line where is and the line where 
is，and 
is the included angle between the line where is and the line where is.Given that 
，we can conclude that 
.From(1)，the following inequality holds.
，(8)
where 
is the polar angle corresponding to ，and 
is the polar angle corresponding to .
According to Step 1 and Step 2，the searching range of the polar angle of is obtained:
.(9)
3.2.2 Dynamical feedback algorithm
This subsection introduces the dynamical feedback algorithm for solving the position of the latter handle.
Based on the position of ，the calculating process of the position of the latter handle is established as follows.If a polar angle 
is selected，then a corresponding point in spiral with respect to 
can be denoted as 
.The coordinate of point in the Cartesian coordinate system is 
.The Euclidean distance between and can be calculated，denoted as 
.Then two cases of and can be obtained.
Case 1:When the difference between and the distance between the two handles is greater than 0:
，(10)
the polar angle of 
should be larger than polar angle of .In this case，the selected polar angle is smaller than the actual 
.A positive number should be added to .On this basis，a parameter 
is introduced，with 
being used as the positive number to be added.Therefore， can be iteratively solved by increasing .
Case 2:When the difference between and the actual chord length is less than 0:
，(11)
the polar angle of should be smaller than polar angle of .In this case，the selected is larger than .A negative number should be added to polar angle .Therefore， can be iteratively solved by decreasing .
With the combination of the above two cases of ，the following equation for iteratively solving is constructed by choosing the initial value as :
，(12)
where 
is the initial value of the iteration， is the polar angle computed at the 
-th iteration，
， is the iterative parameter and 
. is the Euclidean distance between corresponding to the polar angle under the -th iteration and .The stop condition for the iteration to is:
，where 
represents the maximum permissible error.
The framework of the proposed dynamical feedback algorithm is presented as follows.
|
Algorithm:Dynamical feedback algorithm for calculating the position of the latter handle |
|
Input:initial value Output:polar angle
Calculate while Compute
|
4 Simulation Results
In this section，the effectiveness of the proposed dynamical feedback algorithm is illustrated in a simulation environment.
Combining with the data of the 2024 National Mathematical Modeling A problem，the following parameters are selected.
，
(13)
During the iterative process，the paper sets the maximum permissible error as 10-4.The latter handles move along the trajectory of the former handles during the dynamical travel of the bench dragon.As the coil time increases，the position change of the same handle at different moments are mainly related to the polar radius，and the position change of different handles under the same moment are also mainly related to the polar radius.Therefore，discussing the position change of the same handle under different moments has a similar effect to the position change of different handles under the same moment.Based on the dynamical feedback algorithm proposed in the paper，we consider the handle 
of the dragon body as an example.The simulation results of the handle are presented in Fig.3 to Fig.6.
Fig.3 illustrates the variation of the iterative chord length at different moments under the constant iterative parameter 0.15.It can be observed that at 10 s，50 s，100 s，150 s，and 200 s，the number of iterative steps is 4，4，3，3 and 2，respectively.The trend of chord length variation exhibits good consistency.
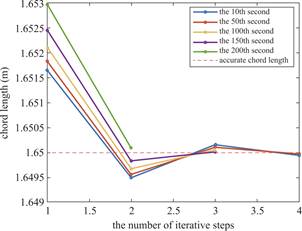
Fig.3 Response curves of iterative chord length at different moments
As shown in Fig.4，it can be found that when the parameter is set to 0.2425，the discrepancy between the iterative chord length and the exact value gradually increases，ultimately diverging.Therefore，once the iterative parameter exceeds the threshold，the iterative chord length no longer converges to the exact value but diverges.
Fig.5 demonstrates the variation in the number of iterative steps across different iterative parameters at initial time.As the parameter increases，the number of iterative steps decreases to an extreme value and then gradually increases until it reaches a point of divergence.The optimal iterative parameter depicted in Fig.5 is 0.11，corresponding to a total of four iterative steps.
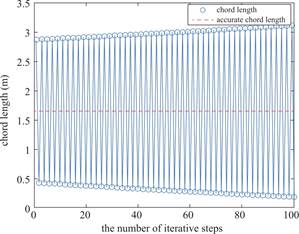
Fig.4 Response curve of divergent chord length
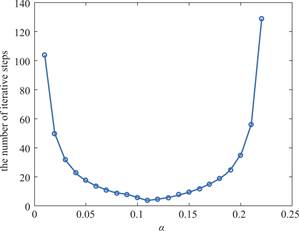
Fig.5 Response curve of the number of iterative steps
Fig.6 shows the changes in the optimal iterative parameters for the third handle at four specific moments.The trend of changes in the number of iterative steps at different moments exhibits superior consistency.It can be observed that at 0 s，50 s，100 s，and 150 s，the optimal iterative parameter is 0.11，0.12，0.13，and 0.14，respectively.Furthermore，as the duration of the bench dragon coiling process increases，the polar radius corresponding to handle diminishes progressively，concurrently with an increment in the optimal iterative parameter.
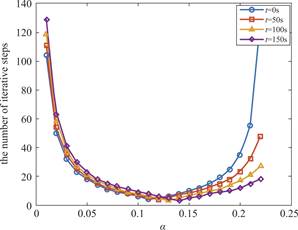
Fig.6 Response curves of the number of iterative steps
5 Improved Algorithm
In this section，the design of iterative parameter is discussed.By introducing a function between the iterative parameter and the polar angle，a functional design of iterative parameter is proposed，which improves the computational efficiency.
From the simulation results of the constant iterative parameter，the optimal iterative parameters change for the different positions corresponding to polar angle.Therefore，the relation between the optimal iterative parameter 
and polar angle is analyzed.
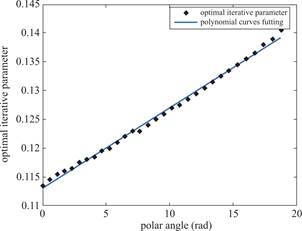
Fig.7 Fitting curve of optimal iterative parameter 
and the polar angle
Based on the content of the former section，the optimal iterative parameters at various moments can be determined.Furthermore，by integrating the relation between the polar angle of the former handle and time，the optimal iterative parameters corresponding to different polar angles can be calculated.The optimal iterative parameter corresponding to each polar angle per second is solved within the 
s.It has been observed that there is a linear relation between the optimal iterative parameter and the polar angles，as shown in Fig.7.Consequently，a linear polynomial is employed for fitting as follows.
(14)
Where 
is the coefficient of 
and 
is the constant term.From the simulation results:
(15)
Building upon equation(12)，the improved iterative equation is derived as follows:
(16)
Fig.8 demonstrates the total number of iterative steps per second of the handle during the coiling process when the iterative parameters are selected as variables and different constants，respectively.When is variable，the total number of iterative steps is significantly lower than when is constant.Particularly，when is 0.12，the difference between the variable and constant is initially small and gradually increases.
The total number of iterative steps within 150 s is calculated and compared between the constant and variable methods，as shown in Table 1.The rate represents the percentage decrease in the total number of iterative steps when using the variable method relative to the constant method.It is observed that the total number of iterative steps decreases by 18.38% when the iterative parameter is variable，compared to a fixed value of 0.12.Consequently，the improved algorithm reduces the number of iterative steps and the computational complexity.
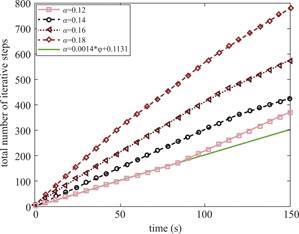
Fig.8 Response curves of the total number of iterative steps
Table 1 Comparison of the total number of iterative steps
|
Iterative parameter |
Total steps |
Rate % |
|
|
Constant |
0.12 |
370 |
18.38 |
|
|
0.14 |
425 |
28.94 |
|
|
0.16 |
572 |
47.20 |
|
|
0.18 |
778 |
61.18 |
|
|
|
302 |
/ |
6 Conclusions
In the paper，the problem of dynamically solving for the position of each handle as the bench dragon coils along the spiral is considered.Based on the characteristic that the distance between two neighboring handles is constant，the dynamic feedback algorithm is used to recursively determine the positions of each handle.The paper provides a detailed analysis of the relation between the iterative parameters and the number of iterative steps.The optimal iterative parameters corresponding to each polar angle are derived.The impact on the convergence speed when the iterative parameters are constant and variable is separately considered.Under the simulation environment，the proposed dynamical feedback algorithm can quickly and accurately calculate the position of each handle.The computational complexity can be effectively reduced by using the improved algorithm.
Conflict of interest:The authors declare no conflict of interest.
[①] *通讯作者 Corresponding author:陈森，senchen@snnu.edu.cn
收稿日期:2024-11-18; 录用日期:2024-12-15; 发表日期:2025-03-28
基金项目:This work is supported by the Young Talent Fund of Association for Science and Technology in Shaanxi，China，under grant No.20230513.
参考文献(References)
[1] Liu C. Historical changes of Jiangxi folk sports “Ta Chengxiang bench dragon”[J]. World of Archives, 2014,(35): 154-155.(in Chinese)
https://doi.org/10.16565/j.cnki.1006-7744.2014.35.018.
[2] Wu L. Aesthetic Review of Huizhou Folk Sports: Based on the Field Investigation of Bench Dragon of Youlong Village[J]. Sports Research and Education, 2021, 36(04): 76-80.(in Chinese)
https://doi.org/10.16207/j.cnki.2095-235x.2021.04.013
[3] Liu S. Investigation and Study on Pu Jiang Bench Dragon[J]. Ethnic Art, 2009,(04): 106-108+115.(in Chinese)
https://doi.org/10.16564/j.cnki.1003-2568.2009.04.022.(inChinese)
[4] Mao R, Wang Q, Wang Z, et al. On the Living Inheritance of Huizhou Bench Dragon in the View of Intangible Cultural Heritage Protection[J]. Martial Arts Studies, 2021, 6(01): 131-132.(in Chinese)
https://doi.org/10.13293/j.cnki.wskx.008789.
[5] Luo J. The Inheritance of Bench Dragon Folk Culture in the Context of Social Development[J]. Todays Literature and Art Creation, 2022,(40): 104-106.(in Chinese)
https://doi.org/10.20024/j.cnki.CN42-1911/I.2022.40.033.
[6] Ibrahim H A, Homidan A S. A derivative-free projection method with double inertial effects for solving nonlinear equations[J]. Applied Numerical Mathematics, 2025, 20955-67.
https://doi.org/10.1016/J.APNUM.2024.11.006
[7] Li X, Liu M. Solving Nonlinear Equation Systems Based on Improved Whale Optimization Algorithm[J]. Engineering and Management Science, 2024, 6(11).(in Chinese)
https://doi.org/10.12238/EMS.V6I11.10005
[8] Popkov S Y. Analytic Method for Solving One Class of Nonlinear Equations[J]. Doklady Mathematics, 2024: 1- 4.(prepublish)
https://doi.org/10.1134/S1064562424601392
[9] Mittal K S, Panday S, Jäntschi L. Enhanced Ninth-Order Memory-Based Iterative Technique for Efficiently Solving Nonlinear Equations[J]. Mathematics, 2024, 12(22): 3490-3490.
https://doi.org/10.3390/MATH12223490
[10] Ozbay H. Introduction to feedback control theory[M]. CRC Press, 2019.
https://doi.org/10.1201/9780203750117
[11] Ross I M, Sekhavat P, Fleming A, et al. Optimal Feedback Control: Foundations, Examples, and Experimental Results for a New Approach[J]. Journal of Guidance, Control, and Dynamics, 2008, 31(2): 307-321.
https://doi.org/10.2514/1.29532
[12] Khalil H K, Praly L. High-gain Observers in Nonlinear Feedback Control[J]. International Journal of Robust and Nonlinear Control, 2014, 24(6): 993-1015.
https://doi.org/10.1002/rnc.3156
[13] Peng N, Yao B, Wang F. Research of H2 Dynamic Output Feedback Reliable Control Against any Fault[J]. Computer Technology and Automation, 2016, 35(01): 1-4.(in Chinese)
https://doi.org/10.16339/j.cnki.jsjsyzdh.2016.01.001.
[14] Wei A, Zhao K. Analysis and Design for Linear Systems with Saturation by Linear Feedback[J]. Control and Decision, 2005,(01): 59-61+68.(in Chinese)
https://doi.org/10.13195/j.cd.2005.01.59.weiar.013.
[15] Long Y, Fan Y. Multiple and Sign-Changing Solutions for Boundary Value Problems of Second-Order Nonlinear Difference Equations[J]. Applied Mathematics, 2018, 31(03): 522-532.(in Chinese)
https://doi.org/10.13642/j.cnki.42-1184/o1.2018.03.034.
Dynamical Feedback Algorithm for Calculating the Moving Position of Bench Dragon' s Path
(1. School of Mathematics and Statistics, Shaanxi Normal University, Shaanxi, Xi' an 710119, China
2. School of Physics and Information Technology, Shaanxi Normal University, Shaanxi, Xi' an 710119, China)
Abstract: The paper considers the problem of determining the position of each handle as the bench dragon coils along the spiral. First, the quantitative searching range of the corresponding polar angle of the handle is given according to the traveling path characteristics of each handle coiled in, offering the initial value for the proposed algorithm. Then, a dynamical feedback algorithm for calculating the position of the latter handle is proposed, which avoids the multi-solution problem of solving nonlinear equations. Furthermore, to promote the computational efficiency, the design of iterative parameters based on varying polar angles is discussed. In the simulation environment, the effectiveness of the proposed dynamical feedback algorithm is illustrated.
Keywords: Dynamical feedback algorithm, iterative parameter, bench dragon
DOI: 10.48014/bcam.20241118001
Citation: ZHENG Wenhuan, ZHENG Shuyi, CHEN Sen, et al. Dynamical feedback algorithm for calculating the moving position of bench dragon' s path[J]. Bulletin of Chinese Applied Mathematics, 2025, 3(1): 1-9.
;
;
;
do
;
;
