谢尔宾斯基分形天线对应分形网络的本征时间及相关问题研究-HTML全文-中国应用数学通报-科学足迹出版社(SFP)

谢尔宾斯基分形天线对应分形网络的本征时间及相关问题研究

彭雨露^1,2, 黄煜可^1,2,*

(1. 北京邮电大学数学科学学院, 北京 102206
2. 数学与信息网络教育部重点实验室 (北京邮电大学) , 北京 102206)

摘要: 本文研究了基于谢尔宾斯基分形天线对应分形网络中随机游走的本征时间及相关问题。访问时间或命中时间H (i, j) 是从节点i出发随机游走到节点j的期望时间。网络G的本征时间定义为H (i, j) 对于任意i, j∈G的数学期望。经典的本征时间计算时, 直接将返回本身的时间记为H (i, i) =0。但在研究电子在分形天线对应分形网络中的随机游走行为时, 考虑电子离开某节点后、首次返回该节点的时间 (自返时间) 是必要的。本文采用了两种研究方法———基于谱理论的特征值方法和基于随机过程理论的马尔可夫链方法———得到修正的本征时间, 并通过一个实例展示了经典的本征时间与修正的本征时间之间的差异正好来源于自返时间。本文展示了分形网络在现代通信中的应用。研究结果有望为分形天线的设计和性能优化提供理论基础。

关键词: 谢尔宾斯基分形天线, 分形网络, 随机游走, 本征时间, 马尔可夫链

DOI: 10.48014/bcam.20250408002

引用格式: 彭雨露, 黄煜可. 谢尔宾斯基分形天线对应分形网络的本征时间及相关问题研究[J]. 中国应用数学通报, 2025, 3(2): 10-18.

文章类型: 研究性论文

收稿日期: 2025-04-08

接收日期: 2025-05-07

出版日期: 2025-06-28

1　Introduction

1.1　Fractal and Fractal Antenna

Wacław Sierpiński(1882—1969)was a renowned Polish mathematician whose work had a profound impact on various fields of mathematics，including topology，number theory，set theory，and geometry.He is best known for his contributions to fractal geometry and self-similar structures.Sierpiński􀆳s name is now closely associated with fractal geometry and self-similarity.His work demonstrated the deep interconnectedness of different mathematical disciplines and continues to inspire research in both theoretical and applied mathematics^[1^].

Our work in this paper is based on a typical example of fractal object called Sierpiński triangle.The Sierpiński triangle is a famous fractal structure that begins with an equilateral triangle.By recursively removing the central inverted triangle at each iteration，the structure evolves into a self-similar shape，see Jaume Anguera et al.^[1^] and Figure 1.

Ashwini et al.^[2^]developed a super-wideband(SWB) Sierpiński triangular fractal antenna，keeping electrical dimension(ED) small and bandwidth dimension ratio(BDR) high.Proposed SWB antenna is useful for multiple bands such as WiMax，WiFi，Fixed Satellite Services，Radio Navigation and Ka bands.Kalaiyarasan et al.^[3^]used some fractal concepts based on Sierpiński triangle to develop various Sierpinski carpet fractal antennas，significantly increasing the bandwidth and gain of the antenna，and improving the return loss.The optimal antenna performs at a frequency associated with 2.45 GHz and is intended for wireless applications.

Further research on fractal antennas needs to address fundamental theoretical issues，primarily the relationship between the geometric features and electrical performance of fractal antennas.All theoretical studies ultimately aim to solve practical engineering problems and apply fractal antenna technology to existing wireless communication markets.This paper will specifically investigate the properties of evolutionary networks generated by the basic fractal structures of fractal antennas.

Fig.1　The first three iterations of Sierpiński triangle

1.2　Fractal Network

A natural extension of the Sierpiński triangle is to generalize it to an M-sided polygon with M≥3，referred to as a Sierpiński-type polygon.In this work，we employ the Sierpiński-type polygon as a fundamental fractal unit to construct a family of evolving networks denoted by .Various complex networks have been built upon self-similar fractal structures，including Sierpinski networks^[4^][5^][6^]，Tree-like branching networks^[7^]，Apollonian networks^[8^]and the hierarchical networks^[9^].

An important problem in studying complex networks is to study their geometric and topological properties.Random walk on networks is a typical dynamic process that has garnered increasing research interest and found widespread applications across various fields of science and engineering.The eigentime，which represents the expected time to travel from one node to another，is a global characteristic of random walk on networks.It reflects the structure and efficiency of the entire network and serves as an important topological property of the network.

Lovász et al.^[10^]summarized methods for calculating the eigentime of a network using eigenvalues.They derived the behavior of random walks by utilizing the eigenvalues and eigenvectors of the graph􀆳s Laplacian matrix，and then calculated the eigentime.However，the eigenvalue method for calculating eigentime does not account for the case where a node returns to itself during a random walk on the network.To more comprehensively study the eigentime on networks，this paper will use Markov chains to derive the mean recurrent time of a node to itself on Sierpiński-type fractal networks.

2　Description of the Model

2.1　The Fractal Object

Let Δ=1，2，…，M denote the alphabet，where M≥3，and arithmetic is taken modulo M，so that M+1=1 in Δ.Consider a filled regular polygon^[6^]K with M sides，whose vertices are defined by a_k=，where k∈Δ.

The corresponding Sierpiński-type polygon is generated by the following iterated function system(IFS):

f_k(x)=λx+(1-λ)a_k，

where the contraction ratio λ is given by

λ=，with l=+1.

In certain studies^[5^]，the Sierpiński-type polygon is characterized as the unique invariant set associated with the iterated function system(IFS){f₁，f₂，…，f_M}.In contrast，this paper focuses on the union of all image sets produced at the ith iteration.Specifically，for any sequence A=x₁x₂…x_i∈Δ_i，we define the composite function f_A==􀳱􀳱…􀳱，and denote the image of the base polygon under this composition by K_A=f_A(K).Each such set K_A represents a scaled copy of the original polygon K with side length λⁱ，corresponding to the ith iteration level.The complete ith-stage approximation of the Sierpiński-type polygon is then given by the union:K_A.

2.2　The Fractal Networks

The construction of an unweighted fractal tree-like hierarchical network based on the Sierpiński-type polygon as the fractal foundation primarily relies on two parameters:the growth generation n of the network and the number of sides m of the Sierpiński-type polygon.Thus，the network is denoted as .The following outlines the construction process of this network.

Firstly，we define the nodes of the network .Based on the previous definition of the Sierpiński-type polygons，we define a one-to-one encoding map φ:K_A→Δⁱ，where K_A→A，with 0≤i≤n. This encoding map allows us to identify all the nodes of ，and subsequently，we can apply a hierarchical encoding scheme to the nodes.

Next，we define the edges of the network .This network is defined as an undirected network，meaning all edges are undirected.Based on the iteration of the Sierpiński-type polygons，we define the set of all nodes generated in the ith generation as the ith layer.Within the same layer，no nodes are connected，implying that there are no edges between them.However，if two nodes from adjacent layers correspond to polygons that share a common contact area，we define an edge between these two nodes.Nodes that belong to non-adjacent layers，even if their corresponding polygons share a common contact area，do not have an edge between them.

Let the number of nodes in each layer of the network be N_i.It is easy to obtain N_i=mⁱ.Then the total number of nodes N_i in a Sierpinski-type fractal network satisfies the following relation:.

Figure 2 illustrates the generation process of the network for the first three generations when m=3.

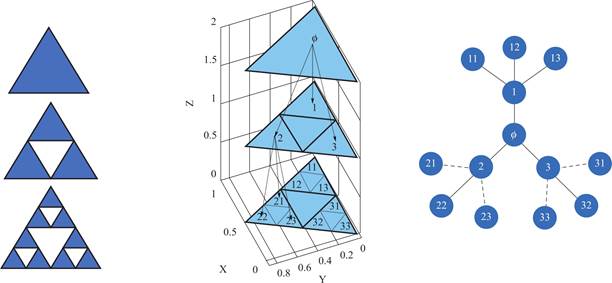
Fig.2　The generation process of the network for the first three generations when m=3

2.3　The Eigentime

In the study of eigentime for random walks on networks，the transition matrix and the Laplacian matrix are often used to describe the dynamic behavior of the random walk.By analyzing the eigenvalues of these matrices，we can further solve for the eigentime.

For the Sierpiński-type fractal network ，Dai et al.^[11^] observed a particular generation of the network and wrote the standard Laplacian matrix for the object network at that generation.Then，by examining the matrix and analyzing its structure，appropriate row transformations were applied to convert the matrix into an upper triangular form.Afterward，the eigenvalues were calculated from the determinant of the transformed matrix.Finally，by applying Vieta’s formulas，the sum of the reciprocals of all the nonzero eigenvalues of the network was computed.This allowed the derivation of an analytical expression for the eigentime of the Sierpiński-type fractal network :H_n~N_n ln N_n，when N_n→∞.

However，when using the eigenvalue method to calculate the eigentime of the network，the case where a node returns to itself is ignored.Therefore，the article proceeds to further investigate the eigentime of the Sierpiński-type fractal network using the Markov chain method.

3　The Markov Chain Method

3.1　The Markov Chain Model

Random walks on fractal networks can be viewed as a Markov chain.A Markov chain is a mathematical model that describes a random process，characterized by state transitions defined by a probability matrix，where the state at each step depends only on the current state.Fractal networks exhibit self-similarity and complex topological structures，and the connection patterns of nodes follow scale invariance.For the random walk on the network，the probability of moving from the current node i to a neighboring node j is typically given by P_ij = ，where k_i is the degree of node i.Therefore，the random walk on a fractal network fully satisfies the definition of a Markov chain.

In this paper，we model the random walk on fractal networks as a Markov chain and use established tools from Markov chain theory to analyze the eigentime.In this context，the return time of a node to itself，denoted as H_n(i→i)，represents the mean recurrent time in the Markov chain.This is the average time required to return to the same state after starting from it.In a Markov chain with a stationary distribution，the average return time of each state is equal to the reciprocal of its steady-state probability.

Let π=be the stationary distribution on the Sierpiński-type fractal network ，where N_n represents the total number of nodes in the network .Then we have H_n(i→i)=.

3.2　The Mean Recurrent Time

3.2.1　Conclusion

Theorem 1　The expression for the mean recurrent time of each node on the Sierpiński-type fractal network is:

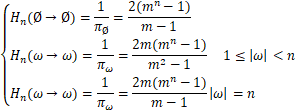
Take n=1 and m=3 for instance，see Figure 3.The theorem above means:

(1)The recurrent time from root node Ø to itself is H_n(Ø→Ø)==2.This means an electron on the Sierpiński-type fractal network = will take 2 steps from root node Ø to itself.In fact，the only paths are Ø→i→Ø，i=1，2，3.This conclusion is clearly true.

(2)The recurrent time from leaf node i to itself is H_n(i→i)==6.This means an electron on = will take 6 steps from leaf node i to itself.

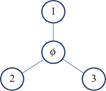
Fig.3　The Sierpiński-type fractal network

3.2.2　Proof of Theorem 1

For a random walk on an undirected graph，the stationary distribution π_i represents the long-term probability that the walk is at node i.

Lemma 2^[¹²^]　

Based on the tree-like hierarchical structure of the Sierpiński-type fractal network ，we can express the degrees of the nodes as follows:

• The degree of all nodes in the intermediate layers is d_int=m+1.

• The degree of the root node is d_Ø=m.

• The degree of the leaf nodes is d_leaf=1.

Based on Lemma 2，the stationary distribution π_i of the nodes on the Sierpiński-type fractal network is expressed as follows:

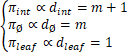
Therefore，

(1)

From the definition of the stationary distribution of the network，it follows that:

π_Ø+(m+m²+…+mⁿ^-1)π_int+mⁿπ_leaf=1(2)

By combining Equation(1)and Equation(2)，it can be derived that:

π_int+(m+m²+…+mⁿ^-1)π_int+π_int=1

Solving it，we get:

π_int=

Therefore，we can obtain the specific expression for the stationary distribution π_i of the nodes on the fractal network :

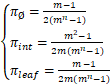
Next，using the formula for the mean recurrent time on a Markov chain，H_n(i→i)=，we can obtain the conclusion in Theorem 1.

4　Numerical Examples

For the Sierpiński-type fractal network ，when n=1 and m=3，we can study the eigentime using two methods:the random walk method and the eigenvalue approach based on the Laplacian matrix.These two methods allow for a more intuitive comparison and analysis of their differences.

4.1　The Eigenvalue Approach

The adjacency matrix of the Sierpiński-type fractal network is:

The degree matrix of is:

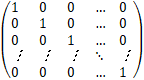
Therefore，the Laplacian matrix of is given by:

L=D-A=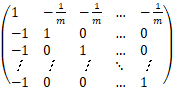

Let M=λI-L=λI-D+A，so

source:si_idp71968464;FounderCES

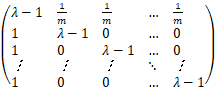
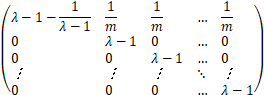
Therefore，the determinant of matrix M can be obtained as:

det(M)=det(λI-L)=(λ-1)^m

=λ(λ-2)(λ-1)^m^-1

Let det(M)=0，we can obtain the eigenvalues of the network as:

λ_i={0，1，1，…，1，2}，i=1，2，…，m，m+1

Theorem 2　The expression for the eigentime of the network is:

For instance，when m=3，we can obtain the eigentime of the fractal network as E_val=.

4.2　The Random Walk Method

For the random walk on the Sierpiński-type fractal network，combined with the Markov chain model in the paper，we can obtain the transition time between the nodes on the network as:

H₁(Ø→Ø)=2

H₁(i→i)=6

H₁(i→Ø)=1

H₁(Ø→i)=×1+[1+1+H₁(Ø→i)]

H₁(Ø→i)=5

H₁(i→j)=H₁(i→Ø)+H₁(Ø→j)=1+5=6，i≠j

Based on the formula for the stationary distribution on the Sierpiński-type fractal network，H_n(i→i)=，we can classify and discuss different pairs of nodes.

Firstly，for the case where each node starts from itself and returns to itself，the expected time is

E₁=E_Ø+E_i=1×××2+3×××6

=+=1

Then，for the case of random walks between different nodes，the expected time is

E₂=E_Øi+E_iØ+E_ij

=3×××5+3×××1+6×××6

=++1=

In summary，the eigentime of the Sierpiński-type fractal network obtained based on the definition of random walks is:

E_def = E₁+ E₂=

4.3　Conclusion

When n=1 and m=3，the eigentime of is E_val==E₂;and the modified eigentime of is E_def= E₁+ E₂= .The difference between E_val and E_def is expectation of H_n(ω→ω)，ω∈{ϕ，1，2，3}.Obviously，the difference between the classical and modified eigentimes is from the mean recurrent time.

5　Applications and Prospects in Fractal Antennas

As mentioned in the introduction，the Sierpiński triangle can be used in modern telecommunication for the development of ultra-wideband antennas^[13^].This paper studies the classical and modified eigentimes in the fractal network corresponding to the Sierpiński fractal antenna.We hope this work can provide a theoretical basis for the design and performance optimization of fractal antennas.

Conflict of interest:The authors declare no conflict of interest.

^{^[①]} *通讯作者　Corresponding author:黄煜可，hyk@bupt.edu.cn
收稿日期:2025-04-08;　录用日期:2025-05-07;　发表日期:2025-06-28
基金项目:This work is supported by the Young Talent Fund of Association for Science and Technology in Shaanxi，China，under grant No.20230513.

参考文献(References)

[1] Anguera, J, Andújar, A, Jayasinghe, J, et al. Fractal Antennas: An Historical Perspective[J]. Fractal Fract. 2020, 4, 3.
https://doi.org/10.3390/fractalfract4010003.
[2] Ashwini, K, Ashish, K, Singh, P. A. P. On the Development of Super-Wideband Sierpinski Triangular Fractal Antenna[J]. Wireless Personal Communications 2024, 134: 119-131.
https://doi.org/10.1007/s11277-024-10890-1.
[3] Kalaiyarasan, R, Nagarajan, G, Seenuvasamurthi, S. Design and Implementation of an Efficient Sierpinski Carpet Fractal Antenna with Defected Ground Structure for 2. 45 GHz Applications[J]. e-Prime-Adv. Electr. Eng. Electron. Energy 2023, 6: 100320,
https://doi.org/10.1016/j.prime.2023.100320.
[4] Barriere, L, Comellas, F, Dalfo, C. Fractality and the Small-World Effect in Sierpinski Graphs[J]. J. Phys. A Math. Gen. 2006, 39: 11739-11753.
https://doi.org/10.1088/0305-4470/39/38/003.
[5] Zeng, C, Zhou, M, Xue, Y. M. Small-World and Scale- Free Properties of the n-Dimensional Sierpinski Cube Networks[J]. Fractals 2020, 28: 2050001.
https://doi.org/10.1142/S0218348X20500012.
[6] Zeng, C, Xue, Y. M, Zhou, M. Fractal Networks on Sierpinski- Type Polygon[J]. Fractals 2020, 28: 2050087.
https://doi.org/10.1142/S0218348X20500875.
[7] Yang, S. S, Fu, H. H, Yu, B. M. Fractal Analysis of Flow Resistance in Tree-Like Branching Networks with Roughened Microchannels[J]. Fractals 2017, 25: 1750008.
https://doi.org/10.1142/S0218348X17500086.
[8] Andrade, J. S, Herrmann, H. J, Andrade, R. F. S, da Silva, L. R. Apollonian Networks: Simultaneously Scale- Free, Small-World, Euclidean, Space-Filling, and with Matching Graphs[J]. Phys. Rev. Lett. 2005, 94: 018702.
https://doi.org/10.1103/PhysRevLett.94.018702.
[9] Niu, M, Li, R. X. The Average Weighted Path Length for a Class of Hierarchical Networks[J]. Fractals 2020, 28: 2050073.
https://doi.org/10.1142/S0218348X20500735.
[10] Lovász, L. Random Walks on Graphs: A Survey[J]. Combinatorics, Paul Erdös Is Eighty 1993, 2: 1-46.
[11] Dai, M. F, Wang, X. Q, Sun, Y. Q, et al. Eigentime Iden- tities for Random Walks on a Family of Treelike Networks and Polymer Networks[J]. Physica A 2017, 484: 132-140.
https://doi.org/10.1016/j.physa.2017.04.172.
[12] Barabási, A. -L, Albert, R. Emergence of Scaling in Random Networks[J]. Science 1999, 286: 509-512.
https://doi.org/10.1126/science.286.5439.509.
[13] Kempkes, S. N, Slot, M. R, Freeney, S. E, et al. Design and characterization of electrons in a fractal geometry[J]. Nature Physics 2018, 15: 127-132.
https://doi.org/10.1038/s41567-018-0328-0.

Research on the Eigentime and Related Problems of the Corresponding Fractal Network of Sierpiński Fractal Antenna

PENG Yulu^1,2, HUANG Yuke^1,2,*

(1. School of Mathematical Sciences, Beijing University of Posts and Telecommunications (BUPT) , Beijing 102206, China
2. Key Laboratory of Mathematics and Information Networks (BUPT) , Ministry of Education, Beijing 102206, China)

Abstract: This paper studies the eigentime and related issues in the fractal network corresponding to the Sierpiński fractal antenna. The access time or hitting time H (i, j) is the expected number of steps before node j is visited, starting from node i . The eigentime of G is the expectation of H (i, j) for all i, j ∈G . Classical eigenvalue method let H (i, i) =0. However, when studying the random walk behavior. of electrons in fractal networks corresponding to fractal antennas, it is necessary to consider the time when electrons leave a certain node and first return to that node (self return time) . This paper adopts two research methods-the eigenvalue method based on spectral theory and the Markov chain method based on stochastic process theory-to obtain the modified intrinsic time, and demonstrates through an example that the difference between the classical intrinsic time and the modified intrinsic time is precisely due to the self return time. This paper shows the applications of fractal networks in modern communications. The research results are expected to provide a theoretical basis for the design and performance optimization of fractal antennas.

Keywords: Sierpiński fractal antenna, fractal network, random walk, eigentime, Markov Chain

DOI: 10.48014/bcam.20250408002

Citation: PENG Yulu, HUANG Yuke. Research on the eigentime and related problems of the corresponding fractal network of Sierpiński Fractal Antenna[J]. Bulletin of Chinese Applied Mathematics, 2025, 3(2): 10-18.