

单节点交叉裂隙油水两相流流动特性实验研究
(北京工业大学城市建设学部, 北京 100124)
摘要: 单节点交叉裂隙是离散裂隙网络的基本组成单元。本文通过实验方法对单节点交叉裂隙模型中油水两相流流动特性进行了研究。将模型按角度不同分为十六组, 在每组实验过程中依次改变油、水相流速, 实验时控制油、水相流速一直在低流速范围内。使用高速摄像机对实验中流体的流动过程进行记录, 并对结果进行详细分析。在低速流条件下, 油水两相在裂隙中呈弹状流。同时考虑油水相流速和裂隙交叉角度对水段长度和水油段长度比的影响。采用蠕动泵转速代替流速进行讨论, 结果表明: 对于同一交叉裂隙角度模型, 当水泵转速不变时, 水段长度随油泵转速增大逐渐减小, 二者呈幂函数的形式变化。当油泵转速不变时, 随着水泵转速的增大, 水段长度和水油段长度比逐渐增大, 分别呈线性和幂函数形式变化。在不同油泵、水泵转速下, 裂隙交叉角度对水段长和水油段长度比的影响规律不同。
关键词: 单节点交叉裂隙, 油水两相流, 弹状流, 水段长, 油段长, 水油段长度比
DOI: 10.48014/bcce.20231201002
引用格式: 杨崎浩, 李博, 王治强, 等. 单节点交叉裂隙油水两相流流动特性实验研究[J]. 中国土木工程通报, 2024, 2(1): 1-12.
文章类型: 研究性论文
收稿日期: 2023-12-01
接收日期: 2024-01-01
出版日期: 2024-03-28
0 引言
石油开采和储运过程中经常会出现油水两相流现象。低渗透裂缝性油藏的开发随着石油勘探的深入日益增多。在开采过程中,注水将原油驱替到岩体裂隙中[1-4],油水两相通过裂隙合并后共同流动到采收井[5]。如图1所示为岩体中的交叉裂隙,从图中可以看出岩体中的交叉裂隙具有许多不同的几何形态,这些交叉裂隙组成了岩体中的裂隙网格。在这种情况下,油水两相在裂隙中流动时,其两相流动形态主要受到裂隙的交叉角度大小和油水流速大小两个主要因素的影响[6,7]。另一方面,流体在岩体中裂隙的流动状态对于流体在岩体内的裂隙网络中的流动有重要影响[8]。因此,研究裂隙交叉角度和油、水相流速对两相流流动特性的影响具有重要意义。
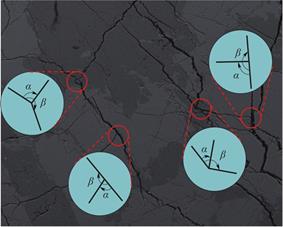
图1 岩体中不同几何形态的交叉裂隙
Fig.1 Cross fractures of different geometries in rock mass
离散裂隙网络(DFN)模型是一种用于描述裂缝的先进方法,其被广泛应用于裂隙介质中两相流动特性的相关研究[9,10]。在对于介质内离散裂隙网格进行研究时,应重点关注离散裂隙网格的重要基本组成单元—单节点交叉裂隙。如图2所示,一进一出、一进两出、两进一出和两进两出这四个流动形式是流体在单节点交叉裂隙中流动的四个基本流动形式。其中,重点对于两进一出这一流动方式进行研究。该流动方式主要包括两条进口裂隙和一条出口裂隙,油相、水相等流体由各自的进口裂隙流入并汇聚于裂隙交叉口,之后共同流出,由于微尺度效应,两相共同流出时会受到表面张力的作用,Zhao等[11]在流动充分发展区域观察到弹状流、单分散滴状流、液滴群流、平行流和环状流5种流型,其中弹状流相比之下更为稳定且较易获得,弹状流型下的两相流动特性已经被许多国内外学者大量研究[12-19]。
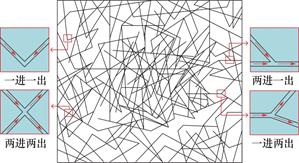
图2 离散裂缝网络(DFN)模型
Fig.2 Discrete fracture network(DFN)model
裂隙介质内裂隙交叉角度对于两相流流动特性的影响已经被广泛研究,其中T型和Y型微通道是两相流在裂隙中流动的两个主要的通道类型。研究发现,当两相在裂隙中流动时,微通道的类型会影响两相流的流动类型[12]。其中,平行流更容易出现在Y型微通道内,而弹状流更容易在T型微通道中形成。研究表明,在弹状流型下,当两相流动时分散相以液滴的形式出现,其中角度会影响其液滴尺寸,根据刘赵淼等人的研究[13],当Y型的角度在180°以内时,角度不影响分散相液滴尺寸,另一方面,当角度减小时,液滴生成时间会加快。Y型角度为180°时,液滴生成时间最长,生成的液滴尺寸最大。Steegmans等[14]发现相比于T型微通道,Y型通道会得到更小的分散相液滴。当前的研究表明,当两相在裂隙中交汇时,裂隙交叉角度会影响两相的碰撞方向,影响液滴的生成过程,进而对液滴尺寸产生重要影响。
弹状流型下,经研究表明,分散相液滴尺寸还会受到两相流速影响。Gupta等[15]研究发现,在T形微通道中分散相液滴形成会受到两相流速的影响,且两相流速在很大程度上会影响液滴的尺寸。当控制两相流速的数值大小不变时,Madhvanand等[16]在Y型微通道的研究背景下发现,随着液滴流速逐渐增大,分散相液滴的尺寸逐渐减小。当两相流速的数值大小发生变化时,Cherlo等[17]研究发现,在T形微通道内,随着连续相流速逐渐增大,液滴的尺寸逐渐减小。屈健等[18]研究发现当硅油流量为固定值时,液滴尺寸随水相流量增大而增大。目前,国内外学者主要对于固定角度下流速与分散相液滴尺寸的关系进行了研究,然而在实际的岩体工程中,岩体中交叉裂隙的角度不是固定不变的。此外,研究表明在两相流动过程中,油相所占比例主要影响采油效率,而分散相液滴尺寸和连续相液滴尺寸之比对油相所占比例有较大影响。因此,研究裂隙交叉角度和油、水相流速对分散相液滴尺寸和两相液滴尺寸比的影响是非常重要的。
本文对于裂隙介质内单节点交叉裂隙中油水两相的流动特性进行了研究,所研究的流动形式为两进一出。首先,将模型按角度不同分为十六组,分别进行实验。其次,每组实验过程中依次改变油、水相流速,实验时需控制水、油相流速的大小一直在低流速范围内。最后,实验过程中用高速摄像机记录流体的流动过程,并对于拍摄结果使用相关分析软件进行详细分析。分散相液滴尺寸用水段长来定义,油、水两相液滴的尺寸之比用水油段长度来定义。实验后对于数据进行分析,讨论了裂隙交叉角度和油水两相流速与水段长、油段长长度比之间的关系。讨论了在哪种条件下,采油效率最高。
1 实验模型和实验流程
1.1 实验模型和装置
本次实验中所使用的模型由有机玻璃(PMMA)材料制作而成。PMMA材料所制作出的裂隙模型相比较于岩石材料所制作出的裂隙模型更为精确。除此之外,还具备可视化的优势,使得实验时观测更为精确便利。但是PMMA材料和岩石材料在材料参数方面有着不同,而流体在裂隙中流动主要与裂隙的形状相关,因此可近似忽略材料参数对实验结果造成的影响。在两个有机玻璃板上雕刻相同的单节点交叉裂隙,并使用亚克力胶黏剂将二者进行粘贴,组成实验所需模型。两玻璃板组成的雕刻裂隙截面用于表示裂隙的开度。模型裂隙截面的形状为矩形,开度为2.0mm×5.0mm,三条裂隙均长 10.0cm,以确保两相流在裂隙中充分流动。
图3所示为四种根据角度进行分类的单节点交叉裂隙模型。如图4所示,为了更好地分析角度因素对试验结果的影响,本次研究对模型的角度进行了详细描述。模型的三条裂隙依次为进油裂隙、进水裂隙和出口裂隙,其中油相通过进油裂隙流入,水相通过进水裂隙流入,二者合并后共同通过出口裂隙流出。将出口裂隙所在直线定义为基准线,进油裂隙与出口裂隙之间夹角用α(0°<α≤180°)表示,进油方向如图所示。进水裂隙与出口裂隙之间夹角用β(0°<β<360°)表示,进水方向如图所示。油相,水相共同流出的方向如图所示,表示为流动方向。图5所示为本实验模型的α、β角度分布情况,从图中可以看出,不同的裂隙中的进水、进油裂隙的位置不同,即α、β不同。本实验根据α、β角度的不同共分为十六组实验。

图3 实验所用的单节点交叉裂隙模型
Fig.3 Single-node cross fracture model used in experiments
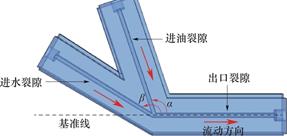
图4 单节点交叉裂隙模型α、β角度的定义
Fig.4 Definition of angle α and β of single-node cross fracture model
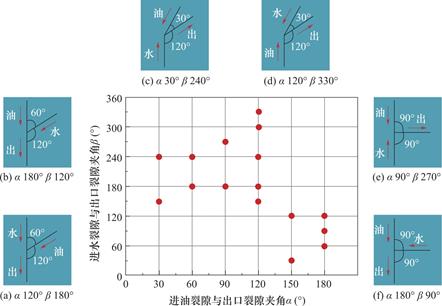
图5 实验模型的α、β角度分布情况
Fig.5 Distribution of α and β angle of experimental model
图6所示为本研究中所使用的实验装置。油相采用食用油进行实验,测得其密度为0.968g/cm3,水相使用自来水进行实验,为便于实验过程中能够通过颜色对于油相和水相进行区分,将适量红墨水与自来水混合放入水箱中,测得其密度为1.055g/cm3。实验过程中通过实验装置右侧油箱旁的数字选择面板调节油相流速,通过实验装置左侧水箱旁的数字选择面板调节水相流速。油、水两相均通过PVC软管流入模型内。在模型的进水裂隙、进油裂隙和出口裂隙处分别雕刻圆形孔洞,与PVC软管相连接并固定密封,其中三个裂隙的开度应严格小于PVC软管的内径,以便于油、水两相能够充分流入模型中的裂隙。打印尺子并将其粘贴在出口裂隙处,以便于量取出口裂隙中的水段长度和油段长度。模型应始终处于水平状态以防止入口和出口之间产生压力差,从而对实验结果造成影响。将高速摄像机安装在模型上部,实时记录两相流动过程。
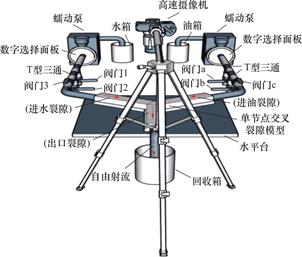
图6 实验装置
Fig.6 Experimental device
图7为蠕动泵转速与流速的关系示意图。蠕动泵转速用n表示,流速用v表示。当n分别取3、5、8、10、15和20rpm时,实验测得了油相和水相v的大小。从图中可以看出,当n不变时,油相与水相v之间的数值大小相差较小。因此,可以假定在实验过程中,在蠕动泵转速固定时,油相和水相的流速近似相等。从图中还可以看出,油相和水相的流速大小都随着n的逐渐增大呈线性增大。本实验共包括16组不同的转速实验。
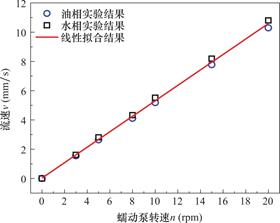
图7 蠕动泵转速与流速的关系
Fig.7 Relation between speed and flow rate of peristaltic pump
1.2 实验流程
首先,将实验装置右侧油箱旁的蠕动泵打开,并将蠕动泵的转速通过数字选择面板调节至实验要求大小。其次,将阀门c打开,使得油相流入模型内,并从进油裂隙流入,当油相流入到裂隙交叉口时将被分为两部分,一部分通过出口裂隙流出并由回收箱回收,另一部分会流入进水裂隙。当模型中的裂隙都充满油相时,通过实验装置将裂隙中的空气排净。油相从进水裂隙流出后,操作步骤如图8所示。首先,使阀门3处于开启状态,使阀门1,2处于封闭状态。将T型三通和软管在a处进行断开,使得油相流动至T型三通,并从a处流出。其次,将装置左侧水箱旁的蠕动泵打开并通过数字选择面板将蠕动泵转速调节至实验要求大小,使得水相通过软管流动至a处。将T型三通与软管在a处相连接。由于在连接的过程中会引入空气并产生气泡,从而会
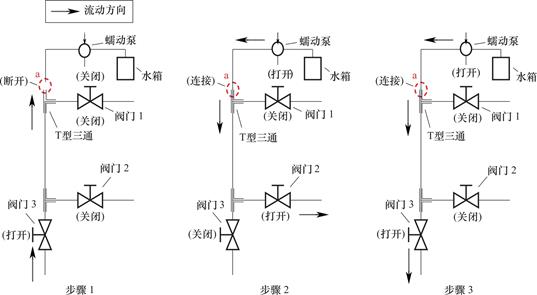
图8 实验过程中排气处理
Fig.8 Exhaust treatment during the experiment
使得实验结果存在误差,所以在实验开始之前应按要求将空气排净。之后开启阀门2,封闭阀门3,水相将软管里的气泡和油相一并驱动到阀门2处流出。等待气泡全部排出干净后,打开阀门3,保持阀门2关闭,油相被水相沿软管驱替并流至模型。水相通过进水裂隙流入模型,并与进油裂隙中流入的油相在裂隙交叉口处交汇,之后共同从出口裂隙流出,再进行回收。试验结束后,对实验装置和设备进行清理,吹干等,以用于下一组实验。固定α、β角度,通过实验装置中的数字选择面板改变装置两侧的蠕动泵转速,进行下一组实验。全部转速完成后,改变α、β角度,重复上述实验。
本次实验排除了空气的影响,以避免模型出现油水气三相流。主要是通过:(1)在实验开始之前,空气充斥在模型的裂隙中。然后,打开油箱一侧的蠕动泵,使油相流入模型裂隙,同时驱替空气流动。当油相充满三条裂隙后,模型中已无空气残留。(2)当软管与T型三通连接到a处时,空气会进入软管。在软管中出现油水气三相流后,关闭阀门3,打开阀门2。此时,油气两相将从软管中被水相躯替并排出。为保证裂隙中为油水两相流,待空气排净后打开阀门3,关闭阀门,使水相流入模型。
2 实验结果与讨论
图9所示为油水两相在出口裂隙中的流动形式,两相的流动形式为弹状流。表面张力作用导致油相和水相之间的相界面形成弯液面,弯曲方向朝向油相,此弯液面可近似视作球面。油相两侧凹液面的球面中心间距离为油段长,用lo表示。水相两侧凸液面的球面中心间距离为水段长,用lw表示。水段与油段长度之比为水油段长度比,即lw/lo,用ε表示。
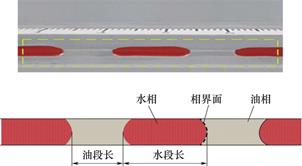
图9 油水两相在出口裂隙中的流动形式
Fig.9 Oil-water two-phase flow pattern in the outlet fracture
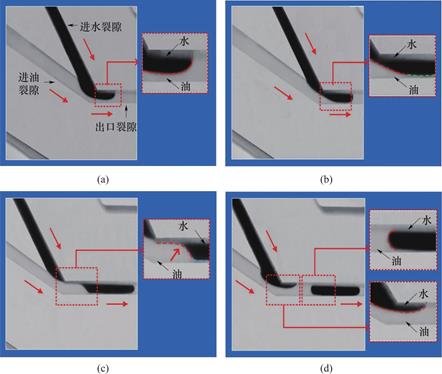
图10 高速摄像机拍摄油、水段形成过程
Fig.10 Formation of oil and water sections by high-speed camera
本实验使用高速摄像机对于油水两相成段过程进行拍摄以便于分析油水段的形成机制。如图10所示,共分为四个阶段。如图10(a),在交叉口处水、油两相交汇并一起流入出口裂隙,称为同流阶段。如图10(b),水相前端逐渐在垂直方向膨胀至充满裂隙,开始逐渐形成水段,水相在两相交汇处受到油相挤压形成颈部,称为成段阶段。如图10(c),由于水相前端满裂隙流动,使油相流动产生较大阻力,被阻挡的油相在两相交汇处压力增大,在两相压差作用下,水相颈部逐渐被压缩,称为挤压阶段。如图10(d),直到两相压差增大至将水相截断,水段脱离水相,从而形成水段,称为脱离阶段。水段生成后,水相会有小幅度后退并再次准备与油相交汇流入出口裂隙,同时油相前端充满出口裂隙开始形成油段。到同流阶段,水相与油相交汇并逐渐挤压油相,直到成段阶段,水相前端充满整个裂隙,将油相截断,从而形成油段。
本文主要对于裂隙交叉角度和油、水相流速这两个主要因素对两相流动特性的影响进行研究。通过改变模型进油、进水裂隙的位置和模型的形状对于裂隙角度这一变量进行控制,角度通过α、β表示。通过改变蠕动泵的转速对于油、水相流速这一变量进行控制,油泵转速大小为实验装置右侧油箱旁蠕动泵转速大小,其可以通过数字选择面板进行调整,油泵转速大小用no表示。水泵转速大小为实验装置左侧水箱旁蠕动泵转速大小,其同样也可以通过数字选择面板进行调整,水泵转速大小用nw表示。本次实验以no、nw代替两相流速进行分析。lw、ε受到两相压差和油、水相流速的影响,而两相压差和流速又分别受到α、β和no、nw的影响。因此,下面详细讨论α、β、no、nw对于lw、ε的影响。
2.1 角度、流速对于水段长的影响
图11为油泵转速no与水段长lw关系的示意图,其中水泵转速nw的取值分别为5、10、15和20rpm。
图11(a)、(b)、(c)、(d)分别为当no的取值为5、10、15和20rpm时,不同α、β角度所对应的lw的值。从图中可以看出,当nw的数值大小保持不变时,lw随着no的增大逐渐减小。
将数据进行拟合后,从图中可以看出,lw随着no的改变呈幂函数的形式变化。将no依次增大时,Δ1、Δ2、Δ3分别表示lw的改变量,从图中可以看出Δ1>Δ2>Δ3。因此,当nw不变时,no越大,no变化相同量时,lw的改变量越小。
图12为当油泵转速no=5、10、15和20rpm时,水泵转速nw与水段长lw关系的示意图。图12(a)、(b)、(c)、(d)分别为当nw在不同取值下(5、10、15、20rpm),不同的α、β角度所对应的lw的值。从图中可以看出,当no的取值保持不变时,lw随着nw的增大逐渐增大。将数据进行拟合后,从图中可以看出,lw随着nw的改变呈线性函数的形式变化。
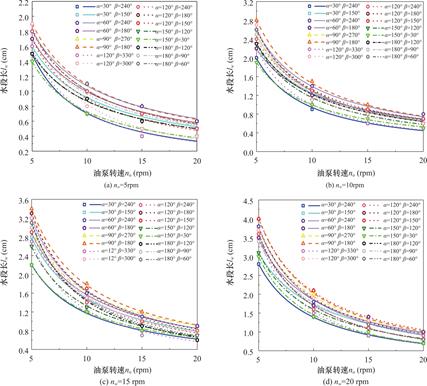
图11 不同nw下,no与lw的关系
Fig.11 The relationship between no and lw under different nw
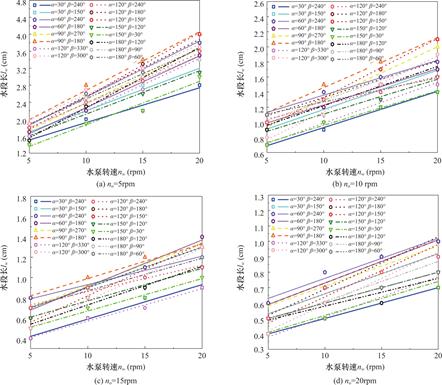
图12 不同no下,nw与lw的关系
Fig.12 The relationship between nw and lw under different no
图13为不同油、水泵转速no、nw下,α、β角度与水段长lw关系的示意图。图中颜色区域代表lw的范围,颜色最深代表lw最小,颜色最浅代表lw最大。当no大小保持不变时,随着nw的增加,各α、β角度处的颜色呈现出依次变浅的趋势,即lw随着nw的增加而逐渐增加。当nw的大小保持不变时,随着no的增加,各α、β角度处的颜色均呈现出依次变深的趋势,即lw逐渐减小。从总体来看,当no的取值为5rpm, nw的取值为20rpm时,各α、β角度处的颜色对比之下均最浅,当no的取值为20rpm,nw的取值为5rpm时,各α、β角度处的颜色对比之下均最深。对于水段长受到α、β角度的影响进行讨论,其中,当no=5rpm nw=20rpm时,在α=120° β=150°和α=90° β=180°处颜色最浅,在α=30° β=240°处颜色最深。当no=20rpm nw=5rpm时,各α、β角度颜色明显无差距,在α=60° β=180°、240°,α=90° β=180°、270°处颜色最浅,在α=30° β=240°,α=120° β=300°、330°,α=150° β=30°处颜色最深。在不同no、nw情况下,α、β角度对lw有着不同的影响规律。
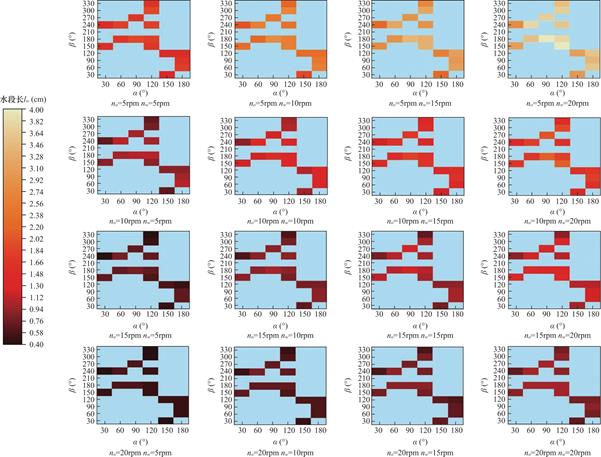
图13 不同no、nw下,α、β与lw的关系
Fig.13 The relationship between α,β and lw under different no,nw
2.2 角度、流速对于油水长度比ε的影响
图14为当油泵转速no在不同取值下(5、10、15、20rpm),水泵转速nw与水油段长度比ε的关系曲线。图14(a)、(b)、(c)、(d)分别为当nw在不同取值下(5、10、15、20rpm),不同α、β角度所对应的ε的值。从图中可以看出,当no的大小保持不变时,随着nw的增大,ε呈逐渐增大的趋势。从图中还可以看出,ε随着nw的改变呈幂函数的形式变化。
图15为不同油、水泵转速no、nw下,α、β角度与水油段长度比ε的关系图。图中颜色区域代表ε的范围,颜色最深代表ε最小,颜色最浅代表ε最大。ε值越大,则水相所占比例在出口裂隙中越大,采油效率越低,ε值越小,则油相所占比例在出口裂
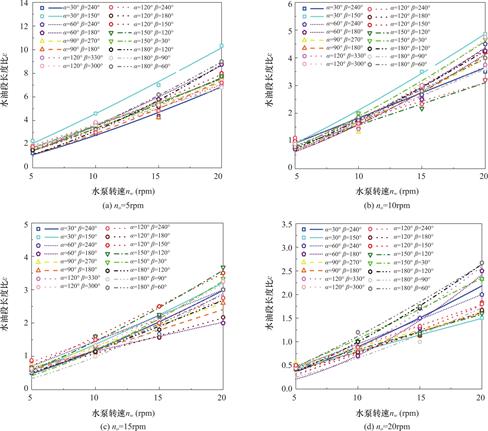
图14 不同no下,nw与ε的关系
Fig.14 The relationship between nw and ε under different no
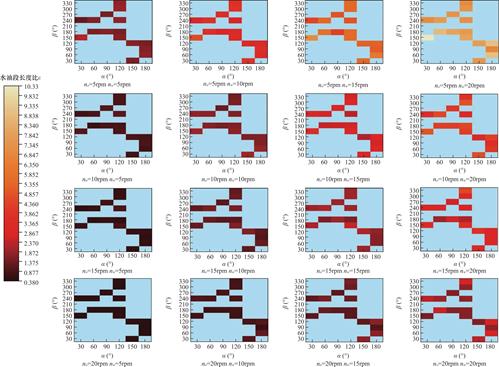
图15 不同no、nw下,α、β与ε的关系
Fig.15 The relationship between α,β and ε under different no,nw
隙中越大,采油效率越高。当no不变时,随着nw的增加,各α、β角度处颜色在对比之下均逐渐变浅,即ε逐渐增加。从总体来看,当no与nw之比大于等于2∶1时,随着α、β角度的变化ε的改变量较小,此时角度因素的影响较小。当no与nw之比小于2:1,ε受到角度因素的影响,在这种情况下,当no=5rpm nw=20rpm时,在α=30° β=150°处颜色最浅,此时ε最大,采油效率最低。当no=15rpm nw=10rpm和no=20rpm nw=15rpm时,在α=180° β=90°处颜色最深,此时ε最小,采油效率最高。在不同no、nw情况下,α、β角度对ε有着不同的影响规律。
3 结论
本文对16组不同α、β角度的单节点交叉裂隙模型在4组不同的油泵转速和4组不同的水泵转速的条件下下进行了流体流动实验,实验研究了裂隙交叉角度和油、水相流速对油水两相流流动特性的影响。本文经分析讨论后得到的结论如下:
(1)当α、β角度大小为固定值时,水段长lw会随着no、nw的变化而变化。当nw数值大小保持不变时,随着no的增大,lw逐渐减小,且lw随no的增大呈幂函数的形式变化。当no数值大小保持不变时,随着nw的增大,lw逐渐增大,且lw随着nw的变化呈线性函数的形式变化。
(2)在不同no、nw情况下,α、β角度对lw有着不同的影响规律。在no=5rpm nw=20rpm时,α=120° β=150°和α=90° β=180°处lw最大。在no=20rpm nw=5rpm时,α=30° β=240°,α=120° β=300°、330°,α=150° β=30°处lw最小。
(3)当α、β角度大小为固定值时,水油段长度比ε会随着nw的变化而变化。no不变时,随着nw增大,ε增大,并且ε随着nw的变化呈幂函数的形式变化。
(4)在不同no、nw情况下,α、β角度对ε有着不同的影响规律。当no与nw之比大于等于2∶1时,ε受角度因素的影响较小。当no与nw之比小于2∶1,在no=5rpm nw=20rpm时,α=30° β=150°处ε最大,采油效率最低。在no=15rpm nw=10rpm和no=20rpm nw=15rpm时,α=180° β=90°处ε最小,采油效率最高。
利益冲突: 作者声明无利益冲突。
[①] *通讯作者 Corresponding author:范立峰,fanlifeng@bjut.edu.cn
收稿日期:2023-12-01; 录用日期:2024-01-01; 发表日期:2024-03-28
参考文献(References)
[1] 王文环. 特低渗透油藏驱替及开采特征的影响因素[J]. 油气地质与采收率, 2006, 13(6): 73-75.
https://doi.org/10.3969/j.issn.1009-9603.2006.06.022
[2] 王家禄, 刘玉章, 陈茂谦, 等. 低渗透油藏裂缝动态渗吸机理实验研究[J]. 石油勘探与开发, 2009, 36(1): 86-90.
https://doi.org/10.3321/j.issn:1000-0747.2009.01.011
[3] 范天一, 宋新民, 吴淑红, 等. 低渗透油藏水驱动态裂缝数学模型及数值模拟[J]. 石油勘探与开发, 2015, 42(4): 496-501.
https://doi.org/10.11698/PED.2015.04.11
[4] 刘海娇, 张旭辉, 鲁晓兵. 基于孔与裂隙网络模型的平行微裂隙对驱油的影响规律研究[J]. 力学学报, 2018, 50(4): 890-898.
https://doi.org/10.6052/0459-1879-18-025
[5] 曲鸿雁, 周生田. 裂缝性油藏开发技术进展[J]. 内蒙古石油化工, 2009, 8: 106-107.
https://doi.org/CNKI:SUN:NMSH.0.2009-08-050
[6] Kosakowski G, Berkowitz B. Flow pattern variability in natural fracture intersections[J]. Geophysical Research Letters, 1999, 26(12): 1765-1768.
https://doi.org/10.1029/1999g1900344
[7] 蒋昌华. 水平管道油水两相流流型研究综述[J]. 工程研究———跨学科视野中的工程, 2013, 5(3): 365-373.
https://doi.org/10.3724/SP.J.1224.2013.00365
[8] Hull L C, Koslow K N. Streamline routing through fracture junctions[J]. Water Resources Research, 1986, 22(12): 1731-1734.
https://doi.org/10.1029/wr022i012p01731
[9] 王建华. DFN 模型裂缝建模新技术[J]. 断块油气田, 2008, 15(6): 55-58.
https://doi.org/CNKI:SUN:DKYT.0.2008-06-018
[10] 刘日成, 蒋宇静, 李博, 等. 岩体裂隙网络非线性渗流特性研究[J]. 岩土力学, 2016, 37(10): 2817-2824.
https://doi.org/10.16285/j.rsm.2016.10.011
[11] Zhao Y C, Chen G W, Yuan Q. Liquid-liquid two-phase flow patterns in a rectangular microchannel[J]. AIChE Journal, 2006, 52(12): 4052-4060.
https://doi.org/10.1002/aic.11029
[12] Dessimoz A L, Cavin L, Renken A, et al. Liquid-liquid two-phase flow patterns and mass transfer characteristics in rectangular glass microreactors[J]. Chemical Engineering Science, 2008, 63(16): 4035-4044.
https://doi.org/10.1016/j.ces.2008.05.005
[13] 刘赵淼, 刘丽昆, 申峰. Y 型微通道两相流内部流动特性[J]. 力学学报, 2014, 46(2): 209-216.
https://doi.org/10.6052/0459-1879-13-228
[14] Steegmans M L J, Schroёn K G P H, Boom R M. Microfluidic Y-junctions: a robust emulsification system with regard to junction design[J]. AIChE Journal, 2010, 56(7): 1946-1949.
https://doi.org/10.1002/aic.12094
[15] Gupta A, Murshed S M S, Kumar R. Droplet formation and stability of flows in a microfluidic T-junction[J]. Applied Physics Letters, 2009, 94(16): 164107.
https://doi.org/10.1063/1.3116089
[16] Madhvanand N K, David W A. Hydrodynamics of liquid- liquid slug flow capillary microreactor: flow regimes, slug size and pressure drop[J]. Chemical Engineering Journal, 2007, 131(1-3): 1-13.
https://doi.org/10.1016/j.cej.2006.11.020
[17] Cherlo S K R, Kariveti S, Pushpavanam S. Experimental and numerical investigations of two-phase(liquidliquid)flow behavior in rectangular microchannels[J]. Industrial and Engineering Chemistry Research, 2010, 49(2): 893-899.
https://doi.org/10.1021/ie900555e
[18] 屈健, 王谦, 何志霞, 等. 矩形微通道内液滴产生和运动特性实验研究[J]. 上海交通大学学报, 2015, 49(1): 86-90.
https://doi.org/10.16183/j.cnki.jsjtu.2015.01.015
Experimental Study on Flow Characteristics of Oil-Water Two-Phase Flow in Single-Node Cross Fracture
(Faculty of Architecture, Civil and Transportation Engineering, Beijing University of Technology, Beijing 100124, China)
Abstract: Single-node cross fracture is the basic unit of discrete fracture network. In this paper, the flow characteristics of oil-water two-phase flow in single-node cross fracture model are investigated by experimental method. The model was divided into sixteen groups according to different angles, the oil and water phase flow rates were changed sequentially in each group and the velocity of oil and water phase were controlled to be in the low velocity flow rate range all the time during the experiment. The fluid flow process was recorded during the experiment by using the high-speed camera and the results were analyzed in detail. Under the condition of low velocity flow, oil-water two phases were slug flow in fracture. Effects of fracture crossing angle and oil-water phase velocity on the length of water section and the ratio of water-oil section length were also considered. The peristaltic pump speed is used instead of flow rate for the discussion, and the results show that for the same cross-fracture angle model, when the water pump speed is unchanged, the length of the water section gradually decreases in the form. of a power function with the increase of the speed of the oil pump. When the oil pump speed is unchanged, as the water pump speed increases, the length of water section increases in the form. of a linear function and the length ratio of wateroil section increases in the form. of the power function. Under different speeds of oil pump and water pump, the influence of fracture crossing angle on the length of water section and the length ratio of water-oil section is different.
Keywords: Single-node cross fracture, oil-water two-phase flow, slug flow, length of water section, length of oil section, length ratio of water-oil section
DOI: 10.48014/bcce.20231201002
Citation: YANG Qihao, LI Bo, WANG Zhiqiang, et al. Experimental study on flow characteristics of oil-water two-phase flow in single-node cross fracture[J]. Bulletin of Chinese Civil Engineering 2024, 2(1): 1-12.