不确定条件下碳酸盐岩地层孔隙压力预测方法研究

向幸运

(中石化华北石油工程有限公司, 郑州 450000)

摘要: 地层孔隙压力在石油钻井中起着至关重要的作用, 是石油钻井中套管方案设计和泥浆比重优化不可缺少的基本参数。利用地震、测井和随钻录井资料可以预测地层孔隙压力。然而, 由于碳酸盐岩地层的隐蔽性和复杂性, 以及地震、测井和泥浆测井资料的固有误差, 地层孔隙压力一直难以准确预测。为了定量描述地层孔隙压力的不确定性, 提出了一种预测地层孔隙压力的概率方法。首先, 根据本文的方法得到了任意井深的伊顿指数和正常压实趋势线分布的统计性质。然后根据蒙特卡罗模拟方法, 生成相应分布特征对应的随机数, 计算任意深度的孔隙压力样本集, 最后选择正态分布拟合任意深度的孔隙压力样本集, 推导出孔隙压力在任意深度下的累积概率分布结果。选取各深度点上累积概率分别为0. 05和0. 95的孔隙压力值, 沿整个井段进行串联, 得到置信度为90%的地层压力区间剖面。实例结果显示, 该方法综合了测井和记录信息, 得到了更准确的孔隙压力预测结果, 不确定性分析后得到的结果为碳酸盐岩地层孔隙压力的预测提供了参考价值。

关键词: 碳酸盐岩地层, 地层孔隙压力, 不确定性, 蒙特卡洛模拟

DOI: 10.48014/cpngr.20240626002

引用格式: 向幸运. 不确定条件下碳酸盐岩地层孔隙压力预测方法研究[J]. 中国石油天然气研究, 2024, 3(2): 5-15.

文章类型: 研究性论文

收稿日期: 2024-06-12

接收日期: 2024-06-20

出版日期: 2024-06-28

1　引言

油气勘探开发中一项至关重要的基础工作便是地层压力的预测，异常压力给石油勘探开发过程带来了众多问题，甚至成为导致许多钻井事故的主要原因之一^[1-3]。而我国在超深碳酸盐岩地层下的油气藏资源含量丰富，近10年探明储量中深层超深层油气资源占50%以上。其中，顺北碳酸盐岩油气藏开发是我国“深地工程”重要主要组成部分，其区域地质环境复杂，具有压力复杂、流体、岩性复杂特征，局部发育异常压力。传统地层压力预测方法对其适应性差、精度低，加之碳酸盐岩地层非均质性强，依靠单一的技术相应难以实现对地层孔隙压力的评价，无法对深部钻井地质风险预测提供压力数据支撑。

国外最早对地层压力进行定量研究分析来自Hottman和Johnson^[4]，他们运用测井方法(声波时差、电阻率)测得的测井资料来获取泥岩性质用于预测地层压力和推算泥岩的正常压实线，从而得到测井观测值与正常值与地层压力梯度的关系，但由于数值计算方法受限，他们仅利用图板法估算出孔隙压力。Forster^[5]基于Terzaghi有效应力理论计算有效应力，提出了等效深度和有效应力两种方法。随后，Matthews、Fertl、Magara等人开始在地层压力预测中引入测井、录井和各类钻井数据^[6-8]。Bingham^[9]在钻井过程中钻速与地层的关系研究中发现，钻速与钻压、转速以及钻头之间存在某种关系;Jodin^[10]在Bingham的研究基础上，先标定了钻井速度，然后提出了一种d指数的预测方法;随后Rehm^[11]提出了dc指数法来对d指数法进行修正改进。Eaton^[12]在前人已有的测井响应与地层压力梯度数学模型基础上，提出了一种基于有效应力理论的计算模型，用于预测泥页岩地层中dc指数、声波时差、孔隙压力与电阻率的关系。该模型认为有效应力与静水压力的比值与测井观测值相对于正常压实趋势线的幂函数关系密切相关。Eaton法由于其优越的预测效果，已广泛应用于实际钻井操作中。当钻井勘探开发往更深、更复杂的地层进行，相关学者逐渐认识到不确定性因素对地层压力预测的影响。Sayers^[13]利用地震资料进行地层压力预测时，首次利用概率分布定性的分析了模型输入参数不确定性对地层压力的影响，并分析了模型输入参数不确定性与地层压力预测结果的关系。Doyen等^[14]使用线性高斯近似和顺序随机模拟方法对地层压力预测进行定量分析，并分析对比了随机方法与确定性结果在估算地层压力后验分布的差异。Moos等^[15]提出了基于蒙特卡洛模拟的钻井定量风险评估方法，他们假设模型输入参数互相独立，且任意深度点上的速度满足正态分布，设置变异系数为5%，获得了地层压力的概率分布模型，并通过随机数据抽取预测出地层压力。Soares等^[16]提出了一种基于地质统计的随机模拟方法，该方法通过概率分布来描述不确定的约束数据，进而通过随机模拟方法进行数值模拟，并将该方法应用在以泥浆密度数据为约束的地层压力预测中。从国内外学者的研究中可见，针对不确定条件下碳酸盐岩地层孔隙压力预测方法的相关研究还鲜有报道，为此，基于传统的地层压力预测方法，本文提供了一种联合利用单井的地质、测井和录井资料，分别描述伊顿指数与正常压实的趋势线的不确定性，依靠蒙特卡洛模拟理论，总结出定量表征碳酸盐岩地层压力的不确定性方法，为预防地质风险和维护井壁稳定提供理论支撑。

2　确定条件下碳酸盐岩地层孔隙压力预测方法

2.1　基于测井资料的地层孔隙压力预测模型

刘宇坤等基于广义胡克定律和Biot多孔介质弹性理论，开发了一种预测超压的理论预测模型，该模型描述了孔隙压力与岩石弹性参数之间的定量关系。其原理是把碳酸盐岩视为弹性体，孔隙中流体含量的变化由应力和孔隙压力引起的:

(1)

式中:ξ代表孔隙流体含量，无量纲;σ_m表示平均有效应力，单位为MPa;P_p表示孔隙压力，单位为MPa;1/H₁表示孔隙压力不变化单位外力作用引起流量变化的率，单位为MPa^-1;1/R表示外力保持不变化单位孔隙压力作用引起流量变化的率，单位为MPa^-1。

基于Biot-Willis有效应力定理推导出了外部应力与孔隙压力之间的关系方程，如下式所示:

(2)

式中:_kk代表岩石三个方向主应力的平均值，单位为MPa;K_d表示骨架体积模量，单位为MPa;K_s表示基质部分的体积模量，单位为MPa;K_f表示流体部分的(孔隙中)体积模量，单位为MPa;ϕ表示孔隙度，以百分比表示;A定义为复合弹性模量组合项。

为了使用上述压力预测模型来预测孔隙压力，需要获取K_d、K_f以及K_s和_kk、ϕ。引入斑块混合充填和流体混合物的充分混合计算得到的孔隙流体等效体积模量更准确，由此，我们可以得到充分流体混合物的等效体积模量通过Wood模型计算方法。

(3)

式中:K_f-wood代表进行了充分的混合后流体的等效体积模量，单位为MPa;K_fi表示各流体成分体积模量，单位为MPa;x_i是组成混合流体各组分的体积百分比，以百分比表示。

实际流体由多种组分构成，通过Wood模型和Patchy模型计算的平均值可表示混合流体的等效体积模量:

(4)

对于岩石基质等效模量，Hill结合Voigt和Reuss的平均值方法改进出了Voigt-Reuss-Hill平均等效模量(VRH等效模量)。

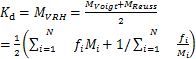(5)

式中:M_i代表单个矿物组分弹性模量(体积或剪切模量)，单位为MPa(常见矿物弹性参数有经验值);f_i表示多矿物所占体积百分比;M_Voigt为Voigt等应力模量，单位为MPa;M_VRH为VRH等效模量，单位为MPa;M_Reuss为Reuss等应变模量，单位为MPa，以百分比表示。

对于岩石干骨架的等效体积模量，Gassmann方程利用四个参数表示饱和流体岩石的体积模量(K_sat)，这四个参数包括K_d、K_s、K_f以及ϕ:

(6)

该类岩石的体积和剪切模量反映了整体的弹性性质，可以通过纵波和横波速度以及密度数据来确定:

(7)

式中:ρ表示饱和岩石的密度，单位为g/cm³;V_p和V_s分别表示纵波速度和横波速度，单位为m/s;μ_sat代表饱和岩石的剪切模量，单位为MPa。

2.2　基于录井资料的地层孔隙压力预测模型

dc指数是根据机械钻速法推导出来的。目前，尽管dc指数仅适用于泥页岩地层，但仍是随钻地层压力监测的最佳应用。1966年，Jorden与Shirley依据Bingham方程，首次提出了d指数方程^[10]:

(8)

式中:R表示机速，单位为m/h;K是地层可钻性，无量纲;D_b代表钻头直径，单位为mm;N表示转速，单位为r/min;W表示钻压，单位为kN;e是转速指数，无量纲;d是钻压指数，即d指数，无量纲。

在保持钻井条件和岩性假设不变(岩性为泥页岩，属于软地层)的情况下，可钻性系数K可取常数1。由于在软地层中转速与机械钻速呈线性关系(即e=1)，因此可以对上述公式进行如下变换:

(9)

d指数前提为钻井液密度保持不变，但实际为了井下安全，在压力过渡带后，须调整增加钻井液密度，d指数随之增加，从而对结果产生较大影响。为了消除影响，Rehm和Meclendon修正d指数建立了dc指数方程:

(10)

式中:ρ_n表示在正常压力地层水的密度，单位为g/cm³;ρ_m表示实际钻井液密度，单位为g/cm³;dc为dc指数，无量纲。

正常压实趋势线及其方程可以根据所选取的目标区域井的正常压力层位或者多口井资料。随后，可以通过趋势线方程来计算或者通过图表查找出相应井深处的dc指数值。在进行地层孔隙压力的Eaton模型计算时，可以利用这些数据:

(11)

式中:P_o表示上部覆盖岩层形成的压力，MPa;P_ng表示正常静水压力，MPa;d_cn为根据正常压实趋势线所获得的深度为H的位置的d_c指数，无因次;n表示Eaton指数，无量纲。

3　不确定条件下碳酸盐岩地层孔隙压力预测方法

当地层孔隙压力符合概率分布状态的话，蒙特卡洛模拟法可以对其进行不确定性量化表征。蒙特卡洛模拟法基于统计抽样原理，通过对随机数进行抽样试验，并对相关随机变量进行统计分析，从而获得用于解决问题的数值解的统计特征值。本文利用测井数据和录井数据，提出了一种量化碳酸盐岩地层孔隙压力不确定性的方法，如图1所示。

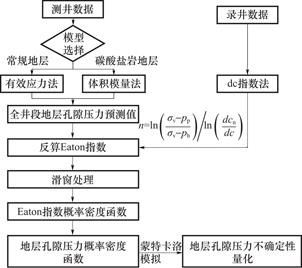
图1　地层孔隙压力不确定性量化流程图

Fig.1　Quantitative flow chart of formation pore pressure uncertainty

根据流程图梳理出了运用蒙特卡洛模拟方法表征的主要步骤:

(1)基于测井资料预测地层孔隙压力

根据地质设计报告，按照地层分层情况选择合适的地层压力测井预测模型，计算出全井段下地层孔隙压力沿井深的数据值(砂泥岩地层为有效应力法，碳酸盐岩地层为体积模量法);

(2)基于录井资料反算Eaton指数值

利用步骤(1)得到的全井段下地层孔隙压力，代入dc法公式进行反演，以计算对应深度的Eaton指数值:

(12)

(3)分析Eaton指数概率分布状态

概率分布拟合的分析样本来自步骤(2)计算所得的不同井深下的Eaton指数值。由层序地层学知识可以知道:“同一沉积环境和地层下的岩石地震或测井相应相似”。因此，本文根据滑动窗口方法(图2)，在同一层组下选取一个深度范围，范围内的地层Eaton指数分析结果便是一个样本，构建对应的样本库。假设在井深范围ΔH内，Eaton指数有2n+1个解释结果，一组测量样本{x_i-n，x_i-n+1，…，x_i+n}由这些解释结果构成，样本区间的深度范围用ΔH表示。

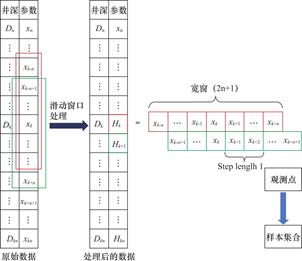
图2　滑动窗口方法示意图

Fig.2　Sliding window method diagram

多项实践和科学试验结果表明，正态分布是一种可描述生产与科学试验关系的概率分布。正常压实曲线斜率和截距的概率密度函数和累积概率分布函数为:

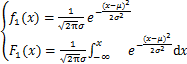(13)

在无穷区间里时Eaton指数呈正态分布的话:

(14)

可得相应地层孔隙压力的概率密度分布:

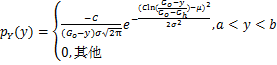(15)

式中:x表示随机变量;μ表示均值;σ表示标准差;C为常数;y表示样本点的地层孔隙压力值，MPa;G_o表示上部覆盖岩层产生的压力梯度，MPa/m;G_h表示静水压力梯度，MPa/m。

(4)建立随机数样本集合

生成符合Eaton指数概率分布的随机计算数的样本集合X_N=[(x_1，1，x_2，1)，(x_1，2，x_2，2)，…，(，)]，N表示蒙特卡洛模拟次数;

(5)建立地层压力样本集合

用步骤(4)所得随机数代入dc法公式，则有地层孔隙压力样本集合Y_h=[顺北X46，y₂，…，y_N]，h表示纵向任意深度位置h，y_i表示在该位置处的一个孔隙压力样本;

(6)定量表征地层压力不确定性

对于步骤(5)得到的集合Y_h进行概率分析统计。首先，任意深度h上地层压力的f_h(y)和F_h(y)采用正态分布拟合获得。然后，选取一个累积概率j，利用F_h(y)确定h位置地层孔隙压力值F_h，j(y)，将各点有序连接便可获得全井段下选定累积概率下的地层压力曲线。如果取j₁=0.05、j₂=0.95，这表示为在j₁和j₂这两个概率下形成了一个置信度为90%的压力区间，即有90%的概率真实地层压力数据在这个压力区间范围内。

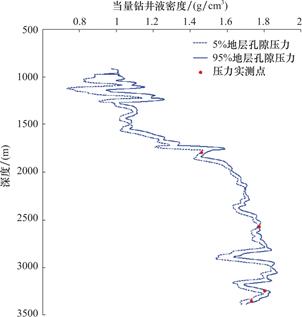
图3　置信度为90%的地层压力区间剖面

Fig.3　Formation pressure section with 90% confidence

4　案例分析

根据顺北区块的实钻结果可知，该区域地质环境复杂，多压力系统并存，钻井风险高，预测难度大，对地层压力系统认识不清，实际与预测压力存在较大误差。对该区域进行精确性钻井液密度选择和针对性井身结构设计带来负面影响，给施工过程带来发生风险事件的风险。顺北X46井量化表征的重点分析步骤如下。

(1)根据顺北X46井地质分层情况以及井身结构数据表，分层组构建了确定条件下地层孔隙压力的统计特征，结果如表1所示。统计结果显示:顺北X46井地层孔隙压力平均值20.73~87.89MPa，标准差0.06~5.12，变异系数0.003~0.076，说明也侧面显示了在碳酸盐岩地层孔隙压力分布范围广，离散程度大，表现出较强的参数不确定性，因此，相应的孔隙压力不确定性量化表征是有必要的。

(2)根据顺北X46井地质设计报告、测井及录井数据结合本文提出的地层孔隙压力不确定性量化方法，通过分地层或组分构建顺北X46井的概率密度分布结果如表2、图4所示。

表1　顺北X46井各层组地层孔隙压力统计特征

Table 1　Statistical characteristics of pore pressure in strata of well X46，Shunbei

地层	代号	深度/(m)	平均值	标准差	变异系数
康村组	N1k	2008~2127	21.586	0.389	0.018
吉迪克组	N1j	2127~2190	21.928	0.239	0.011
苏维依组	E3s	2190~2682	24.645	1.668	0.068
巴什基奇克组	K1bs	2682~3010	28.144	0.496	0.018
卡普沙良群	K1s	3010~3160	31.126	0.524	0.017
哈拉哈塘组	T3h	3160~3532	36.132	1.273	0.035
阿克库勒组	T2a	3532~3680	39.156	2.154	0.055
柯吐尔组	T1k	3680~4168	43.803	2.388	0.055
二叠系	P2+3aq	4168~4208	45.125	1.655	0.037
小海子组	C2x	4208~4461	49.156	3.345	0.068
卡拉沙依组	C1kl	4461~4651	57.395	0.832	0.014
巴楚组	C1b	4651~4683	59.134	2.564	0.043
东河塘组	D3d	4683~4845	60.944	0.862	0.014
克孜尔塔格组	D1-2k	4845~4934	62.236	3.155	0.051
依木干他乌组	S2y	4934~5285	67.123	5.121	0.076
塔塔埃尔塔格组	S1t	5285~6105	72.453	0.165	0.002
柯坪塔格组	S1k	6105~7519	81.751	4.832	0.059
桑塔木-良里塔格	O3s-O3l	7519~7529	77.970	0.072	0.001
恰尔巴克组	O3q	7529~7544	78.334	0.289	0.004
一间房组	O2yj	7544~7708	82.402	1.879	0.023
鹰山组	O1-2y	7708~8760	87.886	1.392	0.016

表2　顺北X46井分层Eaton指数概率分布特征参数

Table 2　Characteristic parameters of stratified Eaton index probability distribution of well X46，Shunbei

地层	代号	深度/(m)	分布形式	平均值μ	标准差σ
康村组	N1k	2008~2127	正态分布(μ，σ2)	1.616	0.156
吉迪克组	N1j	2127~2190	正态分布(μ，σ2)	1.473	0.187
苏维依组	E3s	2190~2682	正态分布(μ，σ2)	1.352	0.026
巴什基奇克组	K1bs	2682~3010	正态分布(μ，σ2)	1.831	0.114
卡普沙良群	K1s	3010~3160	正态分布(μ，σ2)	1.585	0.094
哈拉哈塘组	T3h	3160~3532	正态分布(μ，σ2)	1.550	0.002
阿克库勒组	T2a	3532~3680	正态分布(μ，σ2)	1.917	0.067
柯吐尔组	T1k	3680~4168	正态分布(μ，σ2)	1.286	0.032
二叠系	P2+3aq	4168~4208	正态分布(μ，σ2)	1.757	0.159
小海子组	C2x	4208~4461	正态分布(μ，σ2)	1.754	0.062
卡拉沙依组	C1kl	4461~4651	正态分布(μ，σ2)	1.380	0.106
巴楚组	C1b	4651~4683	正态分布(μ，σ2)	1.568	0.033
东河塘组	D3d	4683~4845	正态分布(μ，σ2)	1.076	0.120
克孜尔塔格组	D1-2k	4845~4934	正态分布(μ，σ2)	1.054	0.053
依木干他乌组	S2y	4934~5285	正态分布(μ，σ2)	1.531	0.131
塔塔埃尔塔格组	S1t	5285~6105	正态分布(μ，σ2)	1.165	0.094
柯坪塔格组	S1k	6105~7519	正态分布(μ，σ2)	1.832	0.002
桑塔木-良里塔格	O3s-O3l	7519~7529	正态分布(μ，σ2)	1.072	0.067
恰尔巴克组	O3q	7529~7544	正态分布(μ，σ2)	1.289	0.032
一间房组	O2yj	7544~7708	正态分布(μ，σ2)	1.879	0.159
鹰山组	O1-2y	7708~8760	正态分布(μ，σ2)	1.392	0.062

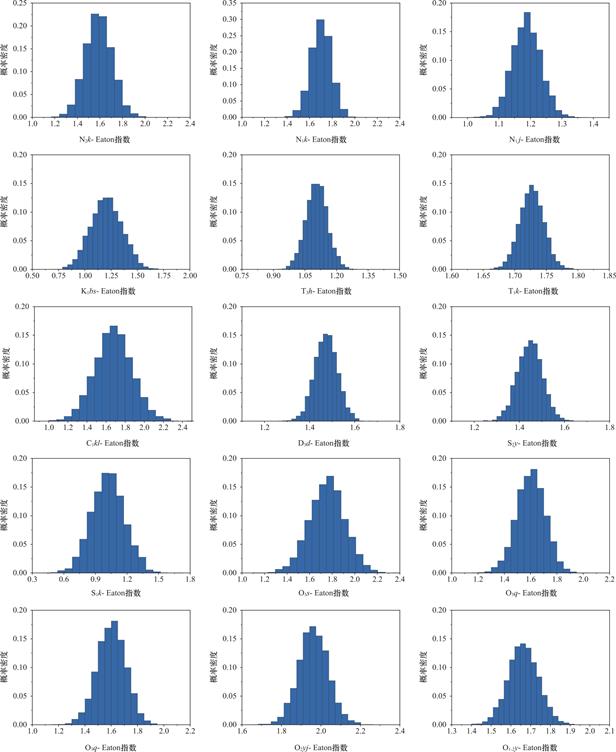
图4　顺北X46井分层Eaton指数概率分布图

Fig.4　Stratified Eaton index probability distribution map of well X46，Shunbei

(3)参照录井数据构建dc指数在正常压实深度650~880m范围内的压实趋势线如图5所示。

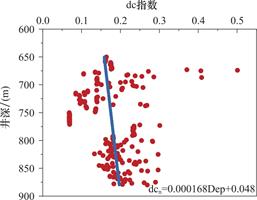
图5　顺北X46井正常压实趋势线

Fig.5　Normal compaction trend line of well X46，Shunbei

(4)选取同一层组一定深度范围内地层Eaton指数解释结果为样本，构建样本库。假设Eaton指数在井深1m范围内有51个解释结果，得到任意深度位置处的地层孔隙压力概率密度及累积概率密度图，顺北X46井3125m处地层孔隙压力概率密度及累积概率密度如图6所示。

(5)最终，置信度为90%地层孔隙压力在顺北X46井通过MATLAB得出了对应的区间剖面，如图7所示。从图中可以看出:确定条件下计算的结果均在构建的地层压力概率统计分布的区域内，证明该方法能够较精确的获得碳酸盐岩地层压力数据，也明确了顺北地区各地层地层压力的分布特征，如表3所示:地层压力梯度0.96~1.34g/cm³(P5水平)，地层压力梯度1.01~1.45g/cm³(P95水平)。

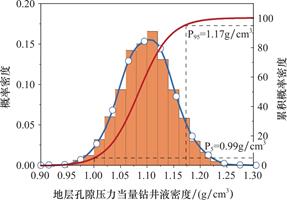
图6　顺北X46井3125m处地层孔隙压力概率密度及累积概率分布图

Fig.6　Probability density and cumulative probability distribution of formation pore pressure at 3125m

of well X46，Shunbei

表3　顺北X46井地层孔隙压力不确定性量化结果

Table 3　Quantitative results of formation pore pressure uncertainty of well X46，Shunbei

地层	代号	深度/(m)	P5	P95
康村组	N1k	2008~2127	1.01~1.05	1.08~1.00
吉迪克组	N1j	2127~2190	1.03~1.04	1.06~1.08
苏维依组	E3s	2190~2682	0.97~1.03	1.01~1.10
巴什基奇克组	K1bs	2682~3010	0.95~1.04	1.06~1.12
卡普沙良群	K1s	3010~3160	0.97~1.07	1.10~1.16
哈拉哈塘组	T3h	3160~3532	0.96~1.09	1.11~1.17
阿克库勒组	T2a	3532~3680	0.93~1.10	1.13~1.19
柯吐尔组	T1k	3680~4168	0.82~1.10	1.05~1.22
二叠系	P2+3aq	4168~4208	1.02~1.07	1.14~1.19
小海子组	C2x	4208~4461	0.97~1.22	1.09~1.34
卡拉沙依组	C1kl	4461~4651	1.17~1.23	1.29~1.35
巴楚组	C1b	4651~4683	1.19~1.23	1.31~1.35
东河塘组	D3d	4683~4845	1.19~1.22	1.31~1.34
克孜尔塔格组	D1-2k	4845~4934	1.19~1.22	1.27~1.34
依木干他乌组	S2y	4934~5285	1.20~1.22	1.23~1.28
塔塔埃尔塔格组	S1t	5285~6105	1.17~1.27	1.24~1.32
柯坪塔格组	S1k	6105~7519	1.00~1.34	1.08~1.45
桑塔木-良里塔格	O3s-O3l	7519~7529	1.07~1.08	1.09~1.09
恰尔巴克组	O3q	7529~7544	1.07~1.07	1.08~1.09
一间房组	O2yj	7544~7708	1.01~1.07	1.07~1.12
鹰山组	O1-2y	7708~8760	1.04~1.08	1.08~1.11

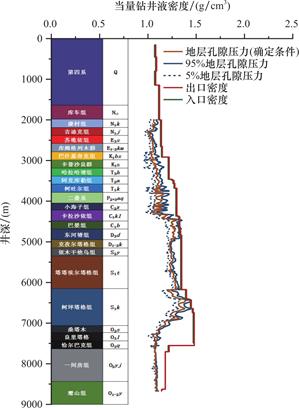
图7　置信度为90%的顺北X46井地层压力区间剖面

Fig.7　Formation pressure section of 90% confidence of well X46，Shunbei

5　结论

本文量化表征顺北地区碳酸盐岩的地层压力不确定性。结合单井测录井信息，对正常压实趋势线和Eaton指数的不确定性进行描述，并基于蒙特卡洛模拟方法，建立了地层压力不确定性定量表征方法。研究结果表明:

(1)本文建立的地层压力预测方法将任意井深位置处的地层压力预测结果从单值转化为含置信度的压力区间，具体来说，顺北X46井3125m井深位置处的地层压力区间为[0.99，1.17]g/cm³，说明该井深位置处的实测地层压力有90%可能落在该区间范围之内;

(2)本文所建立的方法预测得到的全井段地层压力为两条曲线组成的压力区间剖面，在P5水平下，顺北X46井地层压力为0.96~1.34g/cm³;在P95水平下，顺北X46井地层压力为1.01~1.45g/cm³。

(3)与地层压力实测值对比，确定条件下的地层压力预测结果与实测值存在一定差异，只有个别实测压力值落在预测曲线上，而对比建立的含置信度的地层压力范围和顺北X46井地层压力实测值，实测值均在预测范围内，说明建立的地层压力不确定性定量表征方法能有效地反映实际地层压力情况。

利益冲突: 作者声明没有利益冲突。

---

^[①] 通讯作者　Corresponding author:向幸运，hbxbxxy@sina.com
收稿日期:2024-06-12;　录用日期:2024-06-20;　发表日期:2024-06-28

参考文献(References)

[1] 高德利. 复杂地质条件下深井超深井钻井技术[M]. 北京: 石油工业出版社, 2004.
[2] 李琪, 于琳琳, 刘志坤, 等. 钻井风险因素综合评价方法及模型建立[J]. 天然气工业, 2008, 28(5): 120-126.
https://doi.org/JournalArticle/5aec9164c095d710d40193e9
[3] 曾义金, 刘建立. 深井超深井钻井技术现状和发展趋势[J]. 石油钻探技术, 2005, 33(5): 1-5.
https://doi.org/10.3969/j.issn.1001-0890.2005.05.001
[4] Hottmann C, Johnson R. Estimation of formation pressures from log-derived shale properties[J]. Journal of Petroleum Technology, 1965, 17(6): 717-722.
https://doi.org/10.2118/1110-PA
[5] Foster J. Estimation of Formation pressures from electrical surveys-offshore Louisiana[J]. Journal of Petroleum Technology, 1966, 18(2): 165-171.
https://doi.org/10.2118/1200-PA
[6] Mathews W, Kelly J. How to predict formation pressure and fracture gradient[J]. Oil and Gas Journal, 1967, 65(8): 92-106.
[7] Fertl W. Abnormal formation pressures[M]. Amsterdam: Elsevier, 1976.
[8] Magara K. Compaction and fluid migration: practical petroleum geology[M]. New York: Elsevier Scientific Publishing Company, 1978.
[9] Bingham M. A new approach to interpreting rock drill ability[J]. Oil and Gas Journal, 1965, 62(46): 80-85.
[10] Jorden J, Shirley O. Application of drilling performance data to overpressure detection[J]. Journal of Petroleum Technology, 1966, 18(11): 1387-1394.
https://doi.org/10.2118/1407-PA
[11] Rehm B, McClendon R. Measurement of formation pressure from drilling data[C]. Fall Meeting of the Society of Petroleum Engineers of AIME, New Orleans, Louisiana, October 1971: SPE-3601-MS.
https://doi.org/10.2118/3601-MS
[12] Eaton B. The effect of overburden stress on geopressure prediction form well logs[J]. Journal of Petroleum Technology, 1972, 24(8): 929-934.
https://doi.org/10.2118/3719-PA
[13] Sayers C, Johnson G, Denyer G. Predrill pore-pressure prediction using seismic data[J]. Geophysics, 2002, 67(4): 1286-1292.
https://doi.org/10.2118/59122-MS
[14] Doyen P, Malinverno A, Prioul R, et al. Seismic pore pressure prediction with uncertainty using a probabilistic mechanical earth model[C]. SEG Annual Meeting, Dallas, Texas, October 2003: SEG-2003-1366.
https://doi.org/10.1190/1.1817542
[15] Moos D, Peska P, Ward C, et al. Quantitative Risk Assessment Applied to Pre-drill Pore Pressure, Sealing Potential, and Mud Window Predictions from Seismic Data[C]. North America Rock Mechanics Symposium, Houston, Texas, June 2004: ARMA-04-499.
[16] Wessling S, Bartetzko A, Tesch P. Quantification of uncertainty in a multistage/multiparameter modeling workflow: Pore pressure from geophysical well logs[J]. Geophysics, 2013, 78(3): WB101-WB112.
https://doi.org/10.1190/geo2012-0402.1
[17] 刘宇坤, 何生, 何治亮, 等. 碳酸盐岩超压岩石物理模拟实验及超压预测理论模型[J]. 石油与天然气地质, 2019, 40(4): 716-724.
https://doi.org/10.11743/ogg20190403

Research on Pore Pressure Prediction of Carbonate Formation Under Uncertain Conditions

XIANG Xingyun

(Sinopec North China Petroleum Engineering Co. , Ltd. , Zhengzhou 450000, China)

Abstract: Formation pore pressure plays a vital role in oil drilling, and is an indispensable basic parameter for casing scheme design and mud specific gravity optimization in oil drilling. Formation pore pressures can be predicted through the data of seism, logging, and logging-while-drilling. However, due to the concealment and complexity of carbonate formations, as well as the inherent errors in the date of seism, logging, and mud loging, formation pore pressure is always difficult to predict accurately. Thus, a probabilistic method for predicting formation pore pressure is proposed to quantitatively describe the uncertainty of the pressure. Firstly, the method in this paper provides statistical properties of Eaton index and the normal compaction trend line distribution of random well depth. Then, with the Monte Carlo simulation method, the random number corresponding to the distribution features can be generated. And further the pore pressure sample set of any depth can be calculated. Finally a normal distribution is selected to fit the pore pressure sample set of any depth, and the cumulative probability distribution of pore pressure at any depth is derived. The pore pressure values with the cumulative probabilities of 0. 05 and 0. 95 at each depth point were selected and connected in series along the entire well section to obtain a formation pore pressure interval profile with a confidence of 90%. The case study shows that the method, integrating the logging and information recorded, obtains more accurate pore pressure prediction results, which provides a reference value for the uncertainty analysis of pore pressure in carbonate formation.  

Keywords: Carbonate formation, formation pore pressure, uncertainty, Monte Carlo simulation

DOI: 10.48014/cpngr.20240626002

Citation: XIANG Xingyun. Research on pore pressure prediction of carbonate formation under uncertainconditions[J]. Chinese Petroleum and Natural Gas Research, 2024, 3(2): 5-15.