基于压力曲线的水力压裂缝网快速反演方法研究-HTML全文-中国石油天然气研究-科学足迹出版社(SFP)

基于压力曲线的水力压裂缝网快速反演方法研究

鲁良武¹, 刘伟², 张俊成², 张浠^1,*, 李芷¹

(1. 中国地质大学 (武汉) 工程学院, 武汉 430074
2. 中国石油集团川庆钻探工程有限公司井下作业公司, 成都 610051)

摘要: 作为非常规油气储层改造的重要环节, 准确描述压裂缝网空间分布是评估水力压裂效果和计算油气采收率的基础。本文采用了水力压裂流固耦合数值模型表征压裂缝网动态扩展行为并同步输出对应的井口压力响应, 在此基础上集成了可逆跳跃马尔可夫链蒙特卡罗 (RJ-MCMC) 算法与并行计算架构, 构建了一种基于现场施工压力曲线实时反演压裂缝网几何形状的贝叶斯变维反演方法。该方法以缝网内离散裂缝单元 (几何特征与空间分布) 作为随机变量, 基于前一时刻输出的缝网几何形态和该时刻裂缝扩展在不同线程上同时进行随机采样, 结合物理模型与观测数据, 采用Metropolis-Hastings-Green (MHG) 准则筛选随机采样结果, 从而快速生成符合实测井口压力数据的缝网样本集合。随后, 采用贪心算法 (Greedy Algorithm) 选择压力匹配度最高的缝网几何形态为反演结果, 同时优化下一时间步的缝网随机参数以实现后续时间步的高效反演。最后, 为验证反演方法的可行性, 利用西南页岩气H井4段压力数据反演压裂缝网, 并与微地震监测结果对比。结果表明, 反演结果与监测的缝网几何形态在时间和空间上较为一致。必须指出的是, 虽然该反演方法在压力数据选取等方面仍存在改进之处, 但是它无疑为压裂施工缝网几何形态实时评估提供了一个新手段。

关键词: 水力压裂, 变维贝叶斯反演方法, 缝网扩展随机性, 可逆跳跃马尔可夫链蒙特卡洛方法

DOI: 10.48014/cpngr.20250417001

引用格式: 鲁良武, 刘伟, 张俊成, 等. 基于压力曲线的水力压裂缝网快速反演方法研究[J]. 中国石油天然气研究, 2025, 4(2): 23-40.

文章类型: 研究性论文

收稿日期: 2025-04-17

接收日期: 2025-04-27

出版日期: 2025-06-28

0　引言

随着我国能源需求的日益增长，非常规油气日渐成为我国重要能源保障。水力压裂技术因能够改造储层开采条件、提升油气产量，被广泛运用于非常规油气开发^[1-4^]。越来越多的研究表明，储层改造质量与压裂过程中裂缝的数目、几何形状直接相关^[5-7^]。因此，准确获得压裂裂缝的空间分布、几何形态以及演化规律等信息是压裂效果评价、施工方案设计和优化的重要依据。

压裂施工压力曲线作为缝网数据的间接提供者，具有实时性强、数据易得、成本较低的优势。早在1954年，Godbey和Hodges^[8^]就认识到压裂施工压力的重要性，他们认为已知应力的情况下，根据压裂所在地层的实际压力是有可能确定裂缝形态的。1979年，Nolte^[9^]开创性地提出利用压降曲线反演裂缝参数的解析方法，实现了小型压裂测试中裂缝几何参数的定量计算。随后，Nolte和Smith^[10^]通过分析加砂时对数压力随对数时间变化的趋势特征判断裂缝扩展状态。经过几十年的发展，基于压力数据的裂缝诊断方法已形成完整的理论体系，大量研究证实其反演结果在工程精度与时效性方面均能满足现场需求^[11-13^]。然而，其本质仍是基于离散时间节点或特定施工阶段的静态参数表征，仅能定性分析某一时刻的缝网几何形态，缺乏对缝网形态的时空演化轨迹连续刻画的能力，难以支撑“地质-工程一体化”的精细化压裂设计需求。

20世纪80年代，Crockett和Cleary等^[14-16^]通过匹配测量压力历史实时反演储层模量、流体滤失系数等参数，并基于三维裂缝模型动态反演裂缝几何参数。但因其采用单裂缝模型假设，无法用于裂缝富集的页岩油气藏中复杂裂缝的实时反演。2024年，盛广龙等^[17^]提出了一种将缝网形态作为流体流动特征，通过匹配现场压力数据反演缝网几何形态。该方法分为两个步骤:首先基于模拟压力和实测压力的误差利用同时扰动随机近似(SPSA)算法对裂缝长度进行粗拟合;在确定裂缝长度后，考虑了裂缝扩展方向的随机性，连续模拟缝网扩展，并选择模拟压力与实测压力误差最小的缝网几何形态为最终结果。在此基础上，Jia等^[18^]利用微地震监测数据和施工压力曲线联合约束建立了裂缝长度的优化方法，包括约束缝网扩展方向和裂缝长度，得到了同时符合压力曲线和微地震数据的缝网几何形态。然而，上述方法为了满足反演实时性，没有采用流固耦合的裂缝扩展模型，而其压力计算模块采用动态渗透率等效模型替代真实裂缝导流能力演化过程。虽有效表征了缝网宏观形态特征，但牺牲了对缝网的宽度、压力等关键物理量的解析能力。这种“形态优先”的反演策略在非常规储层工程设计中存在潜在风险。

此外，缝网扩展涉及到天然裂缝的并入，如图1。天然裂缝形成受到地质环境、应力状态等诸多因素的影响，是一个高度随机的过程^[19^]，使得压裂缝网扩展同样具有高度随机性。通过引入随机函数和分形概率指数等方法随机选择范围内的裂缝无法充分表征缝网扩展的随机性。基于贝叶斯框架的MCMC方法因其能够充分表征目标参数的不确定性而被广泛应用于地球物理反演问题中^[20^]。2017年，Somogyvári等^[21^]基于离散裂缝网络(DFN)模型利用RJ-MCMC(Reversible Jump Markov Chain Monte Carlo)算法处理地下水网络反演过程中模型维度变化，通过拟合示踪剂穿过岩体的实验数据，成功反演了离散复杂缝网。随后两年，Somogyvári^[22^]又基于该方法，通过拟合现场测量的温度数据，成功反演了Waiwera地热储层的裂缝几何形状。RJ-MCMC方法在地下水网络反演领域的成功应用为水力压裂缝网反演提供了新的思路。

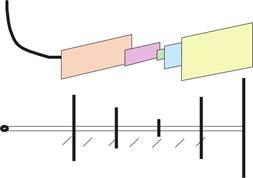
图1　水力裂缝与天然裂缝并入示意图

Fig.1　Schematic diagram of natural fractures

merging into hydraulic fractures

本文拟建立一种能够反映缝网动态扩展物理过程，并考虑缝网扩展随机性的反演方法。首先，为提高计算效率，采用缝高恒定的PKN裂缝模型结合位移不连续法、有限体积法建立缝网扩展物理模型，该模型考虑了天然裂缝分布、裂缝汇合、缝间应力干扰、裂缝入口流量的重新分配、射孔孔眼压降、暂堵、流固耦合等与缝网形成相关的物理过程，能够在表征缝网几何形态的同时迅速给出对应的井口压力值;其次，裂缝扩展的不确定性由缝网内离散单元的几何特征和空间位置表征，利用rj-MCMC方法在现有缝网几何形态的基础上添加随机裂缝单元(随机几何特征与空间位置)获得新缝网形态，结合MHG(Metropolis-Hastings-Green)准则获得表征缝网后验分布的样本集合，通过贪心算法(GA)确定该时间段的缝网几何形态。最后，为了验证反演方法的正确性，利用西南某页岩气井的实测压力数据反演缝网形态和扩展模式，通过与微地震监测结果对比来检查反演结果的可靠性。

1　缝网扩展物理模型

本文提出的压裂缝网反演算法同样由正演模型和反演模型构成。正演模型为用于表征缝网几何形态，并同步给出对应井口压力值的缝网扩展物理模型，在满足计算实时要求的同时，能够精确描述裂缝扩展过程中的流固耦合等关键物理过程。此外，缝网扩展物理模型是基于离散裂缝单元的数值模型，缝网内裂缝单元(几何特征与空间位置)为后文建立反演模型的随机参数。

考虑到缝网扩展物理模型作为正演模型被反复使用，为减少计算成本，对其进行如下简化:

① 储层岩石均质且具有渗透性，缝网被限制在厚度足够大的储层内，即缝网内只存在PKN裂缝;

② 暂堵作用仅发生于水平井筒区域，暂堵材料运移范围被约束在靠近注入段的前半部分水力裂缝，远端水力裂缝不受暂堵影响。

③ 裂缝通过单元进行离散，新增裂缝通过单元端点并入缝网，缝网内各单元都与井筒相连;

④ 水力压裂裂缝长度远大于裂缝高度和宽度，裂缝内的流体流动可以简化为一维模型;

⑤ 压裂液为不可压缩牛顿流体，支撑剂在缝网内均匀分布，会对携砂液的黏度产生影响;

⑥ 水力压裂裂缝形成枝叶状裂缝，各水力裂缝间不允许连通。

1.1　岩石变形方程

本文基于PKN裂缝解析模型的椭圆截面假设，对缝宽在z方向上进行积分平均，建立单元i内部的流体压力p_i与宽度之间的关系。由于缝网扩展涉及到多裂缝的相互作用，原始方程必须考虑裂缝相互作用造成的应力变化。缝宽与压力关系的具体形式为:

p_i--=α_iW_i(1)

式中:E'为岩石的平面应变模量，Pa;W_i为裂缝沿高度方向的平均宽度，m，W_i=w(x，z，t)dz，其中w(x，z，t)为单元的裂缝宽度，m;h为储层厚度，m;α_i为推导获得的相关系数，与选择的裂缝模型相关，对于PKN裂缝模型，α_i=，;为裂缝相互作用在单元i产生的正应力，Pa;所有应力以受压为正;为远场地应力在裂缝单元i引起的正应力，Pa。

采用二维位移不连续法计算裂缝间相互作用力。位移不连续法仅需离散裂缝表面便可计算整个岩石区域的应力场而被广泛应用^[23^]。裂缝平衡方程为:

=U^k+W^k(2)

=U^k+W^k(3)

式中:K为水力裂缝单元和天然裂缝单元数量之和;A是Green函数产生的刚阵系数，Pa/m，该系数考虑了裂缝高度的影响;为各裂缝间相互作用引起的切向应力，Pa;为各裂缝间相互作用引起的切向应力，Pa;W^k和U^k分别为单元k高度方向上的平均法向位移(裂缝宽度)和平均剪切位移，m。

通过无量纲化，公式(1)变为:

=α_iW_i++(4)

式中:=p_i，=，=。

1.2　流体流动方程

在水平井分段多簇压裂时，压裂液以压裂段的入靶点为起点，流经井筒，从射孔孔眼进入地层形成水力裂缝，根据流动区域的不同可将其分为井筒流动和缝内流体流动两种主要流动阶段，每个流动阶段都严格遵守质量守恒定律。

1.2.1　缝内流体流动方程

(1)单裂缝流体流动方程

裂缝中流体流动满足Poiseuille定律，因此，流量的表达式为:

q=-(5)

式中:μ'=12μ，μ为流体的黏度，Pa·s。此外，模型考虑了支撑剂浓度的变化对流体的黏度的影响，方程为:

μ=μ₀(6)

式中:μ₀为输入的流体黏度，Pa·s;c为支撑剂浓度;c_s是临界浓度，为0.675。

对公式(5)沿缝高方向上进行积分，并结合PKN裂缝模型的特性，可以得出裂缝单元i的平均流入和流出流量:

(7)

式中:Qⁱⁿ和Q^out为裂缝单元i内流体的流入和流出流量，m²/s;γ=，s^-1;和为流量系数，m²，结合PKN裂缝模型推导获得，=，=。

对于PKN裂缝，用平均宽度来表示的质量守恒方程为:

++=(8)

式中:δ(i)为克罗内克尔δ函数，无量纲，i是单元编号，当微元体与水平井相连，δ(i)=1，否则δ(i)=0;Q_i为裂缝单元内高度方向上的平均流量，Q_i=q_idz，m²/s;δx和δh为微元体的长度与高度，m;为第i簇水力裂缝的注入速率，m³/s;该值的计算涉及到井筒内的流量分配，具体可见1.2.2小节;χ=2C_L，C_L为岩石的Carter滤失系数，m/s^1/2;t₀为初始发生滤失的时刻，s;t为当前时刻，s。

采用有限体积法对方程(8)在空间和时间上进行离散。在时间段(t，t+Δt)内，离散方程为:

(-)=(-)-Q_injδ(i)+L_i(9)

式中:Q_inj为每簇裂缝高度方向上的平均注入流量，Q_inj=，m²/s;Δx_i为单元尺寸，m;Δt为时间步，s;L_i为滤失项，其表达式为:

L_i=(-)(10)

将等式(4)、(7)代入等式(9)并整理为:

α_i_-1-(α_i+α_i+β)

+α_i₊₁=-β-δ(i)+-(11)

其中，

=(+)-(+)(+)+

(+)

=2χβ(-)

=Q_inj/γ;β=Δx_i/γΔt

(2)分支裂缝交叉处的流体流动方程

在模型中，裂缝相交只发生在单元端点。根据裂缝中流体流动，可以定义流动中单元的上下游关系。此外，在裂缝分叉处无满足流体质量平衡。因此，对于s个裂缝单元连接的交点，质量平衡方程为:

γd_i(-)=0(12)

式中:为相交处无量纲压力，Pa。假设相交处不存在能量损失，因此相交处裂缝单元的压力一样;d_i为节点处的单元的水力系数，结合PKN裂缝模型推导获得，m²，d_i=。

求解方程(12)，可得:

=(13)

因此，裂缝相交处各分支裂缝的注入流量为:

=η_id_m(-)(14)

式中:η_i=d_i/d_m。

结合等式(4)、(7)、(9)、(14)可以得到相交点下游单元的质量守恒方程为:

η_id_mα_m+α_i₊₁-

　(η_iα_id_m+α_i+β)(15)

=-β+-

同理，相交处上游单元的质量守恒方程为:

α_i_-1+η_id_mα_m-(16)

　(η_iα_id_m+α_i+β)

=-β+-

其中，

=η_id_m(+--)+

(+--)

=η_id_m(+--)-

(+--)

1.2.2　井筒中的流动方程

在进行水平井分段多簇压裂时，由于井筒及射孔处的压力平衡条件不同，导致每条水力裂缝的注入速率并不相等。因此，在模拟多条水力裂缝扩展时，需要考虑压裂液的动态分配^[24^]。

假设同一个压裂段内存在着 m 条水力裂缝，在忽略井筒储集效应的情况下，单位时间内泵注的流体体积(Q_T)等于单位时间内流入每条水力裂缝的流体体积(Q_v_，i)之和，即质量守恒定律:

Q_T=Q_v_，i(17)

此外，井筒中的流体压力也满足平衡关系，即水平井入靶点处压力p₀等于每条水力裂缝与水平井相连的单元内的压力(p_i)、射孔摩阻(p_pf_，i)和流体从入靶点流至当前裂缝处的井筒摩阻压降(p_cf_，i)之和，平衡方程如下^[25^]:

p_i+p_pf_，i+p_cf_，i-p₀=0(18)

Crump和Conway^[26^]通过实验研究建立了摩阻压降(p_pf_，i)与射孔孔眼参数之间的关系，具体为:

p_pf_，i=ϕ_p_，i(19)

式中:Q_v_，i为第i条水力裂缝入口处的注入速率，m³/s。ϕ_p(i)为第i条水力裂缝射孔的摩擦系数，kg/m⁷，表达式为:

ϕ_p=0.807249(20)

式中:ρ_f为压裂液密度，kg/m³;n_i为射孔数量;C为无量纲流量系数，通常介于0.5~0.9;D_p为射孔直径，m。压裂过程中的暂堵现象通过改变水力裂缝的ϕ_p(i)进行模拟。具体而言，当发生暂堵时，通过减小射孔数来增大射孔摩阻，使得进入该簇水力裂缝的流量减小，以此模拟暂堵对裂缝流量分布的调控效果。考虑到井筒内流动摩阻对流量分配影响较小，且各簇间距较近，忽略各簇之间井筒摩阻，将等式(18)两两相减，可得:

(p_i₊₁-p_i)+Q_v_，i+1²-Q_v_，i²=0(21)

等式(21)为非线性方程组，方程和未知数个数均为m-1，采用Newton-Raphson迭代法将其转化为线性方程组进行求解。当获得前m-1簇裂缝的注入速率，根据等式17可获得第m簇裂缝的注入速率。

方程的边界条件即初始时刻每条水力裂缝的注入速率，假设水平井内的流量均匀分配，即每簇水力裂缝内部的流量相等:

Q_v_，i=Q_T/N(22)

式中:N为裂缝簇数。

1.3　井口压力计算

正演模型还需要给出对应缝网下的井口压力大小。本文利用前文所求的每段第一簇裂缝与水平井连接的裂缝单元压力p₁和射孔、井筒处的压降计算井口压力。由此可得:

p_井口=p₁+ϕ_p(1)Q_v_，i²+p_cf_，1-ρ_fgH(23)

式中:p_井为井口压力，Pa;H为水平井垂深，m;为流体从井口到达每段第一簇裂缝时的压力损失，Pa，表达式如下^[27^]:

p_cf_，1=f(R)(24)

式中:f(R)为雷诺数R的函数，无量纲。其中f^-1(R)=，a=1/[1+(R/2720)⁹]，b=1/[1+(0.0001R/160D)²];l为第一簇射孔与井口的距离，m;D为井眼直径，m。

1.4　裂缝扩展

缝网扩展包括水力裂缝的扩展和天然裂缝的并入。其中水力裂缝的扩展基于断裂力学建立裂缝扩展准则;而天然裂缝的分布、形态通常是随机的，具体并入方法见下节。水力裂缝扩展遵循线弹性断裂力学理论，即在满足断裂韧性准则(K判据)的情况下发生断裂扩展。在多裂缝同步扩展过程中，强烈的裂缝干扰使得裂缝发生非平面扩展。而在本模型中，裂缝的偏转可通过连通天然裂缝的形式表示，因此，水力裂缝呈平面扩展。采用Erdogan和Si对二维情况下型提出的最大周向应力理论作为裂缝的扩展准则:

K_I=E'W_i(25)

式中:Δx为裂缝尖端单元的长度，m。

考虑到部分裂缝有两个尖端，为了减少计算量，单个时间步中只允许在满足条件且应力强度因子更大的一端添加水力裂缝单元，若水力裂缝和天然裂缝的并入位置重合，优先添加水力裂缝。

确定裂缝生长位置后，需要确定水力裂缝单元的几何特征。裂缝单元的长度、宽度均为给定值(长度为2.5m、宽度为1E-5m)。方位角则根据水力裂缝扩展的位置不同而略有不同，若水力裂缝上半翼发生扩展，方位角与相连的水力裂缝单元一致，下半翼方位角则为相连裂缝单元的方位角基础上加π。

此外，当天然裂缝加入缝网后，成为缝网的一部分，其后续扩展同样遵循等式(25)。同时还设定加入缝网的天然裂缝不会同时连通两条水力裂缝，从而避免生成过于复杂的缝网，确保反演计算的速度和稳定性。

1.5　正演模型的求解方法

基于上述方程，对耦合问题进行隐式求解。需要注意的是，由于不是每次调用缝网扩展物理模型时，缝网都会发生扩展，为了避免引起歧义，本节中的求解流程并未包括裂缝扩展方程，而是在后文中以独立的模块在反演流程图中展现(图3紫色虚线框内)。此外，正演模型在整个反演框架中被频繁调用，调用前所需参数已确定，包括基本施工参数、缝网形态以及Q_v_，i等。具体的程序设计思路如下(图3中绿色线框中的流程图):

(i)读取当前缝网形态及各簇水力裂缝的注入速率Q_v_，i(若为初始时间步，缝网为给定的初始形态，Q_v_，i则按式22处理)，缝网形态包括:每个裂缝单元的尺寸(长宽高)、空间位置(单元中心点位置)以及单元角度等信息;

(ii)利用等式(2)~(3)计算每个裂缝单元因相互作用产生的正应力;

(iii)将和Q_v_，i带入质量守恒方程(11)、(15)和(16)，并联列组成可以求解的线性方程组，采用预处理重启广义最小残差法对其求解获得下一时间步的缝网的宽度分布，当宽度趋于稳定后，利用方程(4)计算缝网的压力分布;

(iv)基于步骤(iii)可以获得与井筒相连接的单元内流体压力(p_i)，利用牛顿法求解方程组(21)，获得下一时间步的Q_v_，i，若Q_v_，i稳定，则结果为下一时间步的缝网形态及Q_v_，i，反之回到步骤(iii);

(v)基于步骤(ii)~(iv)的Q_v_，i，采用等式(23)计算出地面的井口压力p_井口。

2　反演模型

2.1　变维反演方法

与固定维度反演问题不同，本文构建的反演方法需要考虑天然裂缝并入缝网的时间和空间位置的不确定性。为此反演模型以缝网内的裂缝单元(几何特征与空间位置)为随机参数，通过在已有缝网几何形态的基础上添加随机参数实现缝网的更新，这决定了反演模型维度会随时间发生变化，即所谓变维反演问题。对于变维反演问题，Green^[29^]提出了从后验概率分布中采样的贝叶斯概念，即rj-MCMC方法(也称Metropolis-Hastings-Green(MHG)算法)。该方法已广泛应用于地球科学等诸多领域^[30^,31^]。

反演模型计算流程与Somogyvári等人的工作流程类似。单个时间步内，在上一个时间步输出的缝网几何形态基础上随机采样;其次，采用MHG准则对随机采样结果进行筛选，获得表征缝网后验分布的样本集合;最后，基于反演决策方法对样本集合进行统计分析，进而确定当前时刻缝网几何形状及下一时间步所需的随机参数。此外，由于整个反演流程严格遵循马尔可夫链的基本性质——即当前时间步的缝网几何形态仅依赖于上一时间步的状态，而与历史演化路径无关。这一特性使得各时间步的样本采集操作可并行化实施，显著提升了计算效率。

2.2　天然裂缝随机采样

水力裂缝在高压流体的驱动下发生扩展，与天然裂缝连通，形成复杂缝网。然而，天然裂缝的空间位置和几何特征的高度不确定性导致缝网扩展呈现显著的随机性。本文通过在给定缝网几何形态基础上，对天然裂缝进行随机采样以表征缝网扩展的随机性。首先，结合地质信息给出天然裂缝几何特征(缝长、缝宽及方位角)在储层内的概率分布(本文中无任何先验信息，为均匀分布);随后，在给定连通节点处进行采样，遍历可能的裂缝几何特征参数，添加天然裂缝更新缝网，利用正演模型计算新缝网的井口压力。通过多次采样，可以获得该节点处添加天然裂缝所引起的压力响应，并通过模拟压力与实测压力之间的误差，确定该位置的天然裂缝。

与传统MCMC方法类似，RJ-MCMC方法的核心机制同样基于接受-拒绝准则，当确定该节点处的天然裂缝几何特征后，需要计算接受系数来判断该天然裂缝是否纳入参数集合，接受系数的计算具体见2.3节。

2.3　样本评估

本文采用MHG算法对采样结果进行评估。通过计算接受系数a来决定新裂缝单元是否纳入样本集合，当接受系数a值小于0~1之间的随机数，则将该天然裂缝单元纳入样本集合，反之拒绝。接受系数的计算公式如下:

α=min(26)

式中:θ为未更新的缝网形态;θ^*为连通天然裂缝后的缝网形态;p(ξ|θ)与p(ξ|θ^*)为似然函数，用于评估实测压力数据ξ与正演模型的模拟结果ξ(θ)之间的误差，等式(27)给出了计算方法;q(θ|θ^*)与q(θ^*|θ)为提议分布，分别表示缝网从θ^*转变为θ及缝网从θ转变为θ^*的概率，(28)和(39)给出了对应的表达式;J为Jacobian矩阵，表示第i个裂缝单元与新生成的单元之间的关系。反演过程中，添加或删除一个单元并不会改变其他单元的参数选择，因此=1^[32^]。

本文假设观测数据与模拟结果之间的误差呈独立且都表现出正态分布，似然函数的表示式为:

p(ξ∣θ)=exp(27)

式中:ξ为实测的井口压力，MPa;ξ(θ)为正演模型计算的井口压力，MPa;σ为方差，本文设为0.5。

由于模型的无偏性，每条天然裂缝被选择概率是相同的。因此，正向过程的提议分布q(θ|θ^*)为:

q(θ∣θ^*)=(28)

式中:N为缝网中可以添加天然裂缝的单元数量。

其逆过程的提议分布为q(θ|θ^*)，表达式为:

q(θ^*∣θ)=(29)

式中:N_s为当前缝网中所有天然裂缝数量。

需要说明的是，2.2节与2.3节的随机采样和样本评估操作采用并行算法加速。具体而言，算法将不同连通节点的采样工作分配给不同线程，同时对不同节点进行2.2节与2.3节的采样和评估操作。而在单个线程上，通过不断重复2.2节与2.3节的操作，直至遍历该线程负责的所有连通节点。基于上述方法快速获得表征缝网后验分布的样本集合。随后，开启2.4节中的反演决策，确定该时间步的最终结果。

2.4　反演决策

缝网扩展是一个动态演化的过程，随着时间步的推进，缝网形态逐渐复杂，天然裂缝与缝网的连通节点(缝网内的裂缝单元)也随之不断增多。由于反演过程中需要在每个连通节点上进行2.2与2.3节中的采样与评估操作，而连通节点数量随裂缝扩展而快速增加，导致了计算量呈现指数式增加，难以保证反演算法的实时性。此外，反演方法根据缝网的更新构成马尔可夫链，数据生成方式符合Jordan^[33^]的决策树方法，即该时间段的决策结果作为下一时间步的初始条件，形成一种递进的动态过程，如图2。综上所述，反演决策需要解决两个问题，即如何将连通节点的数量保持在合理范围内，实现高效采样以及确定该时间步的最终结果，为下一时间步的采样操作提供初始缝网几何形态。

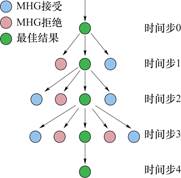
图2　统计分析的决策树归纳方法

Fig.2　Decision tree induction method for statistical analysis

针对第一个问题，本文对缝网内部的连通节点进行动态样本评估，即当某个位置的采样结果连续10个时间步内均未被接受，则认为天然裂缝不可能在该节点处并入缝网，将其从后续时间步需要遍历的连通节点列表中剔除。该方法能够使得反演模型逐步聚焦于更有可能连通天然裂缝的位置，从而显著提高采样的效率。

反演结果的确定采用贪心算法。贪心算法作为一种启发式求解策略，其核心机理在于将整个决策过程分解为多个决策阶段，通过选择每个阶段的最优解逼近全局最优解。该算法容易理解，易于通过编程实现^[34^]，且与数据生成的决策树结构具有天然适配性。具体而言，该算法通过将整个决策过程分解，以每个时间步为决策节点，基于井口压力建立目标函数，即等式(30)，通过最小化目标函数确定缝网几何形态，并将当前最优解作为下一阶段初始条件迭代推进(图2)。

F(θ)=(ξ-ξ(θ))²(30)

此外，为优化缝网复杂度的可控性，本文设置裂缝启动最小因子β(取值范围0~1)表征天然裂缝启裂所需的最小压力贡献阈值。当决策模型选定待评估的缝网后，基于公式(31)计算R，当且仅当R<β时，认为该天然裂缝并入缝网。

R=(31)

3　反演算法

3.1　反演流程

本节将正演模型与反演模型相结合，基于MPI并行框架下，形成完整且可运行的反演算法。基于该算法，可以实现对缝网的快速反演，精确地模拟地下流体流动和缝网扩展行为。该算法采用Bodin和Sambridge^[35^]在地震层析成像问题中使用的双循环结构。具体步骤如下(图3):

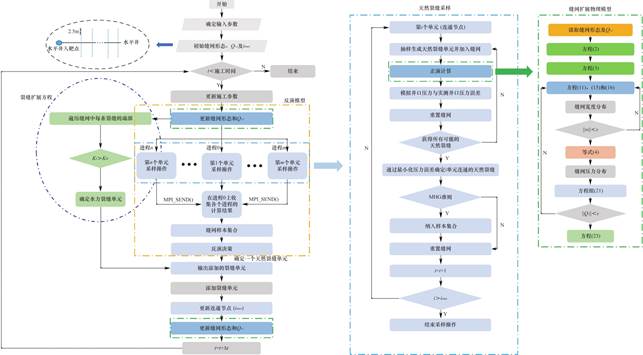
图3　反演算法流程图(紫色线框为水力裂缝生长过程，黄色线框内为反演模型，蓝色线宽内为天然裂缝随机采样过程，绿色线框为正演模型)

Fig.3　Flow chart of inversion algorithm(purple wire frame is hydraulic fracture growth process，yellow wire frame is inversion model，blue line width is natural fracture random sampling process，green wire frame is forward model)

(i)确定模型的输入参数(几何、施工参数)和初始缝网形态，其中参数包括弹性模型、泊松比、断裂韧性、压裂液黏度、压裂液密度、岩石滤失系数、支撑剂密度、裂缝启动最小因子β等参数;初始缝网形态包括每个裂缝单元的尺寸(长宽高)、空间位置(单元中心点位置)、单元角度以及待遍历的连通节点列表等;

(ii)基于当前时间步读取注入速率，支撑剂注入重量，利用公式(6)更新压裂液黏度，计算水平井筒内摩阻损失，以及更新暂堵情况;

(iii)基于上一时间步输出的缝网几何形态和Q_v_，i(若为初始时间步则为给定的初始缝网形态和Q_v_，i)，结合施工数据采用正演模型计算缝网形态未发生变化时的井口压力，同时利用方程(25)确定添加的水力裂缝单元;

(iv)开启内循环，利用反演模型确定将要添加的天然裂缝单元;

(v)将步骤(iii)与步骤(iv)确定的裂缝单元加入到缝网中，更新待遍历的连通节点列表;利用正演模型更新缝网内的压力场合宽度分布，给出对应的压力曲线以及每簇水力裂缝的注入速率，用于下一个时间步的计算;

(vi)判断当前时间步是否大于施工时间，若小于，则进入下一个时间步，回到步骤(i)，否则，反演结束。

3.2　算法验证

在建立反演算法时，采用了PKN裂缝模型提供裂缝截面的宽度轮廓。为了初步验证反演算法，根据PKN裂缝模型的解析解对反演结果进行验证。首先，利用PKN解析解给出时间-压力曲线，通过离散的方式输入到反演程序中。随后，输入相应的材料参数和施工参数，具体见表1。

表1　PKN模型输入参数

Table 1　Input parameters for the PKN model

参数	符号	数值	单位
弹性模量	E	17	GPa
泊松比	ν	0.25	—
断裂韧性	K_IC	1.0	MPa·m^1/2
压裂液黏度	μ	1e-9	Pa·s
压裂液密度	ρ_w	1000	kg/m³
岩石滤失系数	C_L	1E-4	m/s^1/2
支撑剂密度	ρ_p	0	kg/m³
裂缝高度	H	30	m
最小水平主应力	σ_h	0	MPa
最大水平主应力	σ_H	0.1	MPa
裂缝启动最小因子	β	1	—
注入速率	Q_v_，_i	2.5e-3	m³/s
注入时间	t	29	s

考虑到PKN裂缝模型仅适合用于裂缝长度远大于裂缝高度(至少三倍以上)的情况。因此，并未对比二者初始阶段的解，而是让裂缝扩展一段时间后进行对比。从图4可以看到，PKN模型计算净压力的相对误差最大不超过0.04%，并且随时间的波动非常小，解析解与反演解的净压力相对误差先增大后减小，最大值不超过6.5%，二者的一致性也是能够保证的。

在使用反演算法进行计算时，发现天然裂缝并未启动，这是因为驱动主裂缝扩展的压力与输入的解析解非常接近。在这种情况下，任何裂缝的偏转都会在主裂缝扩展路径和两种压力之间产生较大的误差，从而使得反演算法趋向于选择解析解作为最优解。

4　反演结果

4.1　地质工程概况

H井位于大安区块内，井深4620m，垂深4384.84m，井斜87.54°，方位39.79°。实钻B点井深6670m，垂深4380.59m，井斜93.03°，方位36.39°;水平段长2045m(入靶点至人工井底)，水平段箱体钻遇率94.39%;平均杨氏模量为37.4GPa;平均泊松比为0.21;平均最大水平主应力为117.6MPa;平均最小水平主应力为104.2MPa;脆性指数分布在50%~76%，岩石脆性指数较高，易于压裂，有利于缝网的形成。

采用分段体积压裂技术进行施工，将水平段分为28段，每段8~11簇射孔，单段孔数44~50

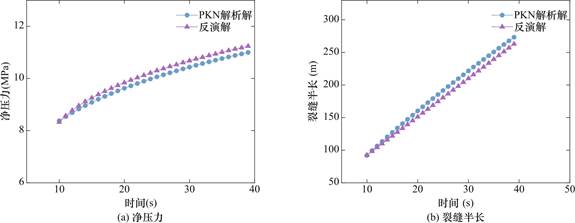
图4　反演结果与PKN解析解比较

Fig.4　Comparison of inversion results and the PKN analytical solution

孔，平均孔径9.9mm。设计施工注入速率为0.26~0.3m³/s，用液强度33~40m³/m，加砂强度3.3~3.8t/m。其中除第一段外，采用暂堵球、暂堵剂于第二次注入期间进行复合暂堵转向。

4.2　输入参数

根据现场水力压裂施工数据、井下压力剖面和相关测井资料，来确定算法的输入参数。由于各段稍有不同，表2仅给出第一段的参数。除此之外，还需要压裂施工过程中的泵注速率、井口压力以及支撑剂重量，分别为图5中的粉红色、蓝色、绿色曲线。

表2　输入参数(现场案例，以第一段为例)

Table 2　Input parameters(field case example:first fracturing stage)

参数	符号	数值	单位
弹性模量	E	37.7	GPa
泊松比	ν	0.21	—
断裂韧性	K_IC	1.0	MPa·m^1/2
压裂液黏度	μ	3.5E-9	Pa·s
压裂液密度	ρ_w	1000	kg/m³
岩石滤失系数	C_L	1E-4	m/s^1/2
支撑剂密度	ρ_p	2600	kg/m³
裂缝高度	H	30	m
最小水平主应力	σ_h	117	MPa
最大水平主应力	σ_H	104	MPa
裂缝启动最小因子	β	0.999	—

4.3　结果与分析

选取H井的第1、10、15和24段的施工数据进行反演计算，并对比反演与实测地面压力曲线，以及反演计算与微震监测得到的缝长、缝网的时空分布和破裂形式，旨在深入了解压裂施工效果，并验证反演算法在模拟实际场景中的可行性与准确性。

在Dell7920工作站上采用60个线程进行反演计算，各压裂段的计算时间为104~147分钟，相对于每段近2~4h的施工时间，算法的实时性得到保证。

4.3.1　地面压力曲线

图5给出了第1、10、15和24段的反演和实测地面压力的对比情况，为更好观察压降过程中实测压力和模拟压力的拟合程度，将二者压降部分进行局部放大。如图所示，两种算法均能准确捕捉压降起始时间节点，且在闭井后的压力差异小于3%。值得注意的是，压力曲线在部分时间段呈现不规则波动(紫色与橙色曲线凹陷处)，这源于支撑剂注入速率的瞬时突变(对应于图5中支撑剂曲线斜率变化点)，导致压裂液黏度产生动态变化，进而引发压力扰动。

观测显示，两种算法的原始反演结果(紫色曲线)存在压力偏差(模拟值低于实测值)，这归因于缝网扩展物理模型未考虑近井筒裂缝扭曲效应——该效应强度由地应力各向异性与射孔方位角共同决定。在明确射孔方案及施工条件下，该压力偏差应不随时间发生变化。通过提取两次闭井阶段的压力值计算闭合压力差A，证实其确实保持恒定。基于此，对原始反演曲线(紫色曲线)进行压力补偿修正(橙色曲线)。修正后压力曲线(橙色曲线)与实测数据的匹配精度通过决定系数R²量化(表3)，结果表明:第1段因实测数据后期异常波动导致R²值偏离外，但在异常波动前，模拟压力与实测压力曲线的拟合度为0.91，除此之外，其余压裂段的R²值均大于0.8。

表3　各段反演井口压力与实测井口压力曲线的拟合程度

Table 3　Fitting degree of inverted vs.measured wellhead pressure curves across stage

段号	R²
第1段	0.49
第10段	0.84
第15段	0.83
第17段	0.81
第24段	0.86
第27段	0.82

同时可以看出，第1段、第17段反演压力数值上稍大于实测压力;第10段、第15段、第24段以及第27段的反演值略低于实测值;这可能是由于实际施工过程中各段之间的“压窜效应”增加了裂缝扩展所需的破裂压力^[36^,37^]。此外，除去第一段外，其余压裂段的第二阶段反演压力明显大于第一阶段，这是由于这部分压裂段在反演过程中于第二阶段模拟暂堵处理，使流体分流，部分裂缝内压力增大。

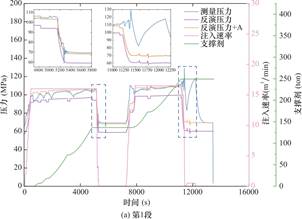
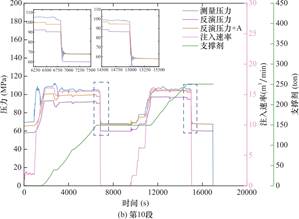
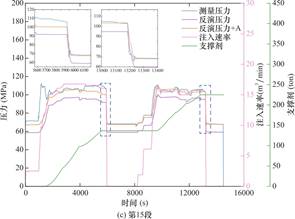
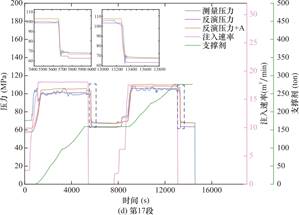
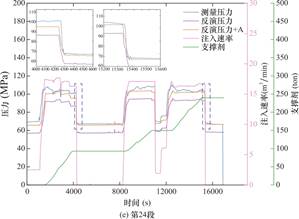
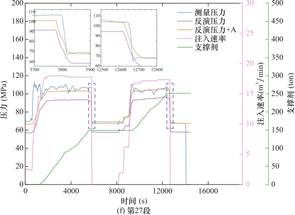
图5　给定泵注历史下反演与实测井口压力曲线的对比

Fig.5　Inverted and Measured Wellhead Pressure Curves under Specified Pumping History

4.3.2　微震云图

微震监测因实时、连续的优点，是现阶段油气开发领域内定量评估水力压裂施工效果的主要方法。虽然其监测结果存在误差，但诸多学者的工作表明，该方法在定性描述缝网几何位置和扩展方向上具有一定可靠性^[38^,39^]。因此，本文针对选取的4段压裂段，将反演结果与现场微震监测结果进行对比，主要围绕缝网几何形态、裂缝时空展布以及裂缝破坏形式三个方面，来验证反演算法的可靠性。

(1)缝网几何形态

第二次泵注结束后，第1、1015、17、24和27段裂缝的3D几何形态的模拟结果如图6所示。不难看出，水力裂缝在压裂过程中得到了充分发育，大多数压裂段的水力裂缝半长可达到150 m，即使是最短的第1段，水力裂缝的半长也达到了125 m;水力裂缝在接近水平井周围的区域内缝宽最大，可达到3~4 mm，并以该区域为中心向外逐渐降低;天然裂缝也得到了扩展，甚至并入了更次级的天然裂缝，形成了缝网;天然裂缝的缝宽普遍较小，不超过0.1 mm。

将反演裂缝缝长与微震监测缝长进行对比的结果如图7所示。分析发现，微地震所获缝长普遍大于反演值，这源于监测技术本质差异——微地震记录的是剪切破裂事件的空间包络，其范围通常大于以张开型破裂为主导的水力裂缝实际导流区域^[40^]。定量评估显示，反演缝长与微震监测结果的相对误差分别为16.67%、18.91%、21.93%、13.43%、10.43%以及2.22%，具有较好的一致性。

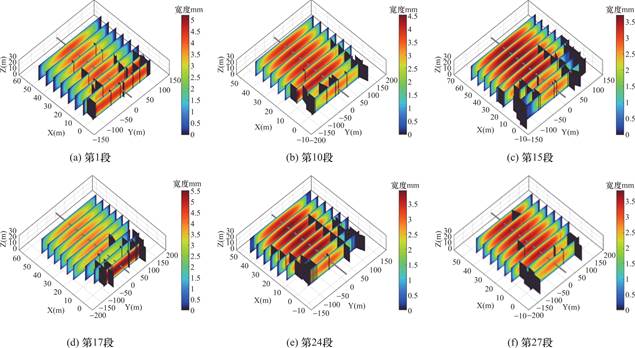
图6　第二次泵注结束时反演裂缝的几何形状

Fig.6　Inverted fracture geometry after completion of the second pumping stage

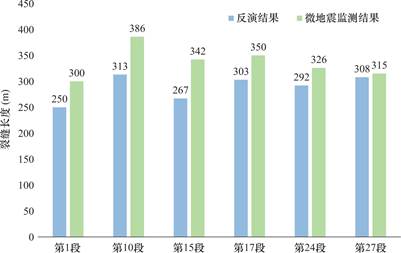
图7　各压裂段水力裂缝的平均反演缝长和微震监测缝长(蓝色为反演结果、浅绿色为微震监测结果)

Fig.7　Average inverted and microseismic-monitored hydraulic fracture lengths for each fracturing stage(blue:inversion results;light green:microseismic monitoring results)

此外，4段压裂段的反演结果显示，天然裂缝集中在水力裂缝某一侧的尖端处以大角度并入缝网，Cooke^[41^]与Zhang^[42^]等在他们的水力压裂模型中也观察到类似的现象，他们认为这种现象是因为裂缝相互作用在水力裂缝表面产生了剪切位移，使得裂缝一侧产生较大的张力，促使裂缝起裂和天然裂缝的并入。这一现象从侧面说明了反演算法虽采用了较为简单的缝网扩展模型，但却可以复现出一些高精度水力压裂物理模型捕捉到的裂缝扩展特征。进一步验证了反演算法的可靠性。

(2)缝网的时空展布

压裂过程中天然裂缝与水力压裂缝网并入，意味着缝网发生变化，同时天然裂缝会在高应力下被激活，无论是张开还是滑移，都会伴随着能量的释放，这一结果直接表现为微震现象的频繁出现。因此，微震监测技术能够大致捕捉到缝网的变化及其空间分布。下面将反演结果中天然裂缝的并入时间和位置信息，与现场实测的微震云进行对比。

为了表述简便，采用如下约定:a.每段微震监测结果中西南侧的水力裂缝为第一簇;b.裂缝时空展布图的方位为上北下南，左西右东。

从图8中可以看出，第1段的微震监测结果表明，在压裂前期，前三簇水力裂缝激活了天然裂缝，到压裂中期，前三簇水力裂缝上的天然裂缝进一步扩展;同时，后三簇水力裂缝也激活了少量天然裂缝;而第1段的缝网几何形态反演结果也表明前三簇水力裂缝在压裂前期和中期均激活了天然裂缝并扩展，后三簇在压裂中期出现少量天然裂缝。第10段与第17段的反演结果表明，前四簇水力裂缝在井筒的东南一侧于压裂前中期激活了一定数量天然裂缝，在压裂后期，前四簇水力裂缝在井筒两侧均激活了部分天然裂缝，但在整个压裂过程中，后三簇水力裂缝均未激活任何天然裂缝;相应的微地震监测结果表明，压裂前中期，天然裂缝集中在前四簇水力裂缝被激活，这与反演结果一致，但在压裂后期，水力裂缝激活了少量天然裂缝，这与反演结果存在差异。对于第15段，不论是微震监测结果还是反演结果，都表明天然裂缝的并入集中发生在压裂的前中期，且激活位置主要位于前四簇水力裂缝，剩余的水力裂缝几乎未激活天然裂缝。第24段的微震监测的结果表明，在压裂前中期，天然裂缝并入位置集中在井筒西北侧的前四簇水力裂缝，而随着压裂施工的进行，前四簇水力裂缝于井筒东南一侧也激活一定数量的天然裂缝。相应的反演结果也能说明这一情况。第27段的反演结果表明，天然裂缝的激活集中发生在压裂的前中期，且激活位置主要位于前三簇水力裂缝，其余水力裂缝仅有少量天然裂缝并入，这与微地震监测结果一致。

综上所述，尽管反演算法与微地震监测结果在局部细节上呈现差异，但反演算法能够有效识别天然裂缝主要激活时段及并入位置，与微地震监测揭示的缝网扩展时空特征具有一致性。

(3)裂缝破坏形式

压裂产生的裂缝扩展方式分为张性破裂、剪切破裂、混合破裂三种。其中，剪切破裂会产生横波，释放的能量相对较大，张性破裂则是产生纵波，释放的能量相对较小，因此微震云可以通过分析能量大小给出单次微震信号对应的破裂特征。通过统计反演得到的缝网内分支裂缝角度信息，对缝网中裂缝的破裂模式进行了归类分析。其中，与水平井平行的天然裂缝被归纳为混合破裂，垂直于水平井的天然裂缝则为张开型破裂，其余方向的裂缝主要呈现剪切破裂。

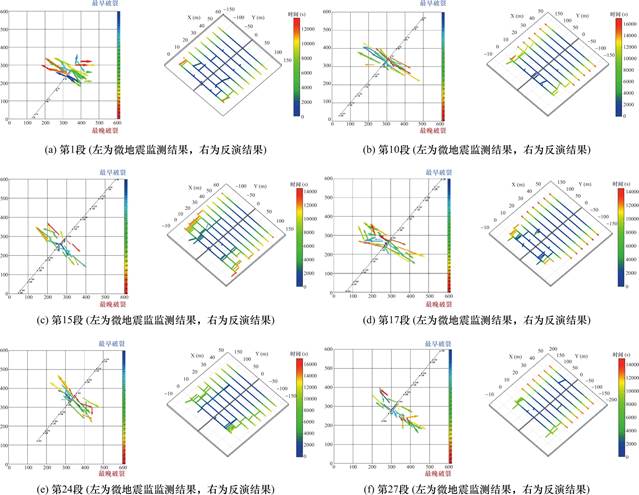
图8　压裂缝网内部裂缝破裂时空分布俯视图

如图9所示，将微震监测结果中的裂缝单次破裂形式与反演结果中的得到的各裂缝的破裂形式进行对比。不难看出，在第1段中，微地震监测结果表明，裂缝以剪切破裂为主，同时伴随一定比例的混合破裂和少量的张性破裂，而反演结果则表明裂缝的破裂模式为混合破裂为主，伴随一定量的剪切破裂与少量张性破裂，但考虑到混合破坏涉及较大剪切变形和相应的能量释放，因此认为裂缝以剪切破裂为主。微地震监测结果表明17段几乎为纯剪切破裂模式，与反演结果的混合破裂为主伴随剪切破裂的模式不同，但是混合破裂中包括一定量的剪切破裂，因此认为该段裂缝以剪切破裂为主。在第10、15、24段中，微地震监测结果表明裂缝为剪切破裂和混合破裂并存，并伴随极少量的张性破裂的模式，反演算法捕捉到了裂缝剪切破裂和混合破裂并存的破裂模式，但并未捕捉到极少的张性破裂。第27段反演结果表明该段裂缝以混合破裂为主，并伴随一定量的剪切破坏;但除此之外，微地震监测还捕捉到极少量的张性破裂模式。

综上所述，虽然反演算法无法捕捉到与微地震监测完全一致的裂缝破裂模式，但能够较好地反映出与微地震监测相符的主要破裂模式，这对指导施工具有积极意义。

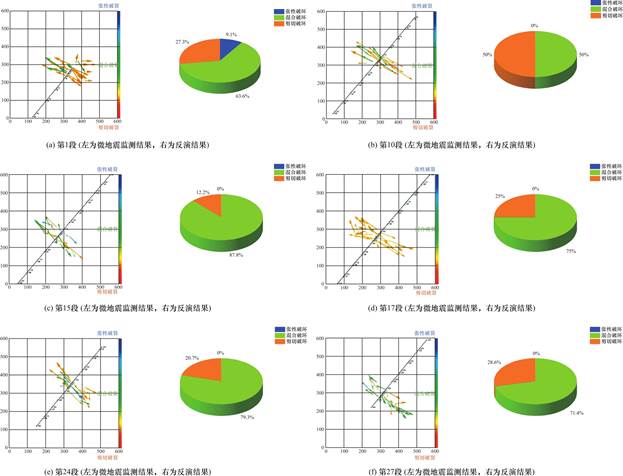
图9　裂缝单次破裂特性分布图

Fig.9　Distribution of single fracture event characteristics

5　结论

本文基于建立的反演算法匹配水力压裂过程中压力的现场实测值，并对压裂过程产生的缝网几何形态进行实时反演。主要结论如下:

(1)通过对裂缝离散化，建立了描述缝网扩展的物理正演模型。模型考虑了天然裂缝分布、裂缝汇合、缝间应力干扰、裂缝入口流量的重新分配、射孔孔眼压降、暂堵、流固耦合等与缝网形成相关的物理过程，能够在表征缝网几何形态的同时迅速给出对应的井口压力值;

(2)基于rj-MCMC方法建立了反演模型，模型以正演模型中的裂缝单元为随机参数，通并行计算，能够快速生成表征缝网后验分布的样本集合。随后采用贪心算法，将整个决策过程分解，以单个时间步为决策节点，通过最小化基于压力误差的目标函数确定该时间步下的最佳缝网几何形态，并通过动态评估策略对采样所需的随机参数进行剪枝，以实现后续时间步的高效反演;

(3)开展H井的现场数据的反演工作。通过反演结果与实测压力数据及微震监测结果的对比表明:反演得到的压力曲线与实测值吻合度较高;反演与微震监测的水力裂缝长度相对误差小于20%;二者的缝网扩展的时空分布基本一致，而且破坏形式也呈现出相似的特征。

本文提出的基于物理模型的反演方法为缝网反演提供了新的思路，该方法仍有许多值得改进之处，将在以后的研究中逐步改进。

利益冲突: 作者声明无利益冲突。

^{^[②]} *通讯作者　Corresponding author:张浠，zhangxi@cug.edu.cn
收稿日期:2025-04-17;　录用日期:2025-04-27;　发表日期:2025-06-28
基金项目:本项研究得到了国家自然科学基金项目(资助号:U23B20156)、国家自然科学基金青年项目(资助号:42107197)、中国石油集团川庆钻探工程有限公司科技项目(资助号:CQ2022B-28-3-4)的资助。

参考文献(References)

[1] 蒋廷学, 卞晓冰, 孙川翔, 等. 深层页岩气地质工程一体化体积压裂关键技术及应用[J]. 地球科学, 2023, 48(01): 1-13.
https://doi.org/10.3799/dqkx.2022.311
[2] 董大忠, 邹才能, 杨桦, 等. 中国页岩气勘探开发进展与发展前景[J]. 石油学报, 2012, 33(A01): 107-114.
https://doi.org/10.7623/syxb2012S1013
[3] 邹才能, 董大忠, 王玉满, 等. 中国页岩气特征、挑战及前景(一)[J]. 石油勘探与开发, 2015, 42(06): 689-701.
[4] 郝伟, 陆努, 王树涛, 等. 页岩气藏数值模拟研究进展[J]. 科学技术与工程, 2016, 16(13): 143-150.
https://doi.org/10.3969/j.issn.16711815.2016.13.025.
[5] FISHER M K, WRIGHT C A, DAVIDSON B M, et al Integrating fracture mapping technologies to optimize stimulations in the Barnett shale[J]. SPE Prod & Fac, 2005, 20(02): 85-93.
https://doi.org/10.2118/77441-MS
[6] FISHER M K, HEINZE J R, HARRIS C D, et al. Optimizing horizontal completion techniques in the Barnett shale using microseismic fracture mapping[C]//SPE Annual Technical Conference and Exhibition. Houston: SPE, 2004: SPE-90051-MS.
https://doi.org/10.2118/90051-MS
[7] MAXWELL S C, URBANCIC T I, STEINSBERGER N, et al. Microseismic imaging of hydraulic fracture complexity in the Barnett shale[C]//SPE Annual Technical Conference and Exhibition. San Antonio: SPE, 2002.
https://doi.org/10.2118/77440-MS
[8] GODBEY J K, HODGES H D. Pressure measurements during formation fracturing operations[J]. Transactions of the AIME, 1958, 213(01): 65-69.
https://doi.org/10.2118/889-G
[9] NOLTE K G. Determination Of Fracture Parameters From Fracturing Pressure Decline[C]//SPE Annual Technical Conference and Exhibition. Las Vegas: SPE, 1979.
https://doi.org/10.2118/8341-MS
[10] NOLTE K G, SMITH M B. Interpretation of Fracturing Pressures [J]. J Pet Technol, 1981(33): 1767-1775.
https://doi.org/10.2118/8297-PA
[11] 姚志远. 利用施工压力曲线评价压裂缝网的复杂度[D]. 北京: 中国石油大学(北京), 2020.
[12] 卞晓冰, 蒋延学, 贾长贵, 等. 基于施工曲线的页岩气井压后评估新方法[J]. 天然气工业, 2016, 36(2): 60-65.
https://doi.org/10.3787/j.issn.1000-0976.2016.02.008
[13] 周彤, 苏建政, 李凤霞, 等. 基于停泵压力降落曲线分析的压后裂缝参数反演[J]. 天然气地球科学, 2019, 30(11): 1646-1654.
https://doi.org/CNKI:SUN:TDKX.0.2019-11-015
[14] CROCKETT A. R, WILLIS R M, CLEARY M P, et al. Improvement of Hydraulic Fracture Predictions by Real- Time History Matching on Observed Pressures[J]. SPE Production & Operations, 1989, 4: 408-416.
https://doi.org/10.2118/15264-PA
[15] CROCKETT A R, OKUSU N M, CLEARY M P. A Complete Integrated Model for Design and Real-Time Analysis of Hydraulic Fracturing Operations[C]//SPE California Regional Meeting. Oakland: SPE, 1986.
https://doi.org/10.2118/15069-MS
[16] CLEARY M P, BUHARALI A M, CROCKETT A R, et al. Computerized Field System for Real-Time Monitoring and Analysis of Hydraulic Fracturing Operations[C]//International Meeting on Petroleum Engineering. Beijing, SPE, 1986.
https://doi.org/10.2118/14087-MS
[17] SHENG GL, ZHAO H, HUANG H, et al. A Real- Time Inversion Approach for Fluid-Flow Fractures in Unconventional Stimulated Reservoirs[J]. SPE Journal, 2024: 29: 1178-1194.
https://doi.org/10.2118/218001-PA
[18] [JIA RX, LI XM, MA XY, et al. Data-Driven Dynamic Inversion Method for Complex Fractures in Unconventional Reservoirs[J]. Lithosphere(2024): n. pag.
https://doi.org/10.2113/2024/lithosphere2023347
[19] 张繁昌, 肖张波, 印兴耀. 地震数据约束下的贝叶斯随机反演[J]. 石油地球物理勘探, 2014, 49(01): 7.
https://doi.org/CNKI:SUN:SYDQ.0.2014-01-026
[20] 蒋星达, 张伟, 杨辉. 地球物理反演问题中的贝叶斯方法研究. 地球与行星物理论评[J], 2022, 53(02): 159-171.
https://doi.org/10.19975/j.dqyxx.2021-042
[21] SOMOGYVÁRI M, JALALI M, JIMENEZ P S, et al. Synthetic fracture network characterization with transdimensional inversion[J]. Water Resour, 2017, 53(06), 5104-5123.
https://doi.org/10.1002/2016WR020293
[22] SOMOGYVÁRI M, KÜHN M, REICH S. Reservoirscale transdimensional fracture network inversion[J]. Advances in Geosciences, 2019, 49: 207-214.
https://doi.org/10.5194/adgeo-49-207-2019
[23] CROUCH S L, STARFIELD A M, RIZZO F J. Boundary element methods in solid mechanics[J]. ASME Journal of Applied Mechanics, 1983; 50(3): 704-705.
https://doi.org/10.1115/1.3167130
[24] WU K, OLSON J. Simultaneous Multifracture Treatments: Fully Coupled Fluid Flow and Fracture Mechanics for Horizontal Wells[J]. SPE Journal, 2015, 20(02): 337-346.
https://doi.org/10.2118/167626-PA
[25] Wu K. Numerical modeling of complex hydraulic fracture development in unconventional reservoirs[D]. 2014.
[26] CRUMP J B, CONWAY M W. Effects of perforation-entry friction on bottomhole treating analysis[J]. Journal of Petroleum Technology, 1988, 40(08): 1041-1408.
https://doi.org/10.2118/15474-PA
[27] CHENG N S. Formulas for Friction Factor in Transitional Regimes[J]. Journal of Hydraulic Engineering, 2008, 134(9): 1357-1362.
https://doi.org/10.1061/(ASCE)07339429(2008)134:9(1357)
[28] ERDOGAN F, SIH G C. On the crack extension in plates under plane loading and transverse shear[J]. Journal of Basic Engineering, 1963, 85(04): 519-525.
https://doi.org/10.1115/1.3656897
[29] GREEN P J. Reversible jump Markov chain Monte Carlo computation and Bayesian model determin-ation[J]. Biometrika, 1995, 82(05): 711-732.
https://doi.org/10.1093/biomet/82.4.711
[30] BODIN T, SAMBRIDGE M, TKALI H, et al. Transdimensional inversion of receiver functions and surfacewave dispersion[J]. Journal of Geophysical ResearchSolid Earth, 2012, 117(B2).
https://doi.org/10.1029/2011JB008560
[31] RAY A, KEY K. Bayesian inversion of marine CSEMdata with a trans-dimensional self parametrizing algorithm[J]. Geophysical Journal International, 2012, 191(03): 1135-1151.
https://doi.org/10.1111/j.1365-246X.2012.05677.x
[32] SAMBRIDGE M, GALLAGHER K, JACKSON A, etal. Trans-dimensional inverse problems, model comparisonand the evidence[J]. Geophysical Journal International, 2006, 167(02): 528-542.
https://doi.org/10.1111/j.1365-246X.2006.03155.x
[33] JORDAN M I. A statistical approach to decision treemodeling[C]//COLT Seventh annual conference onComputational learning theory. New Brunswick: COLT, 1994: 180139. 175372.
https://doi.org/10.1016/B978-1-55860-335-6.50051-9
[34] 陈嘉, 徐添杰, 庄国献. 基于贪婪算法的战时航空油料调度优化模型研究[J]. 电子质量, 2023, 6: 82-85.
https://doi.org/10.3969/j.issn.1003-0107.2023.06.019
[35] BODIN T, SAMBRIDGE M. Seismic tomography withthe reversible jump algorithm[J]. Geophysical JournalInternational, 2009, 178(3): 1411-1436.
https://doi.org/10.1111/j.1365-246X.2009.04226.x
[36] 刘乃震, 张兆鹏, 邹雨时, 等. 致密砂岩水平井多段压裂裂缝扩展规律[J]. 石油勘探与开发, 2018; 45(06): 1059-1068.
https://doi.org/10.11698/PED.2018.06.14
[37] 才博, 唐邦忠, 丁云宏, 等. 应力阴影效应对水平井压裂的影响[J]. 天然气工业, 2014, 34(07): 55-59.
https://doi.org/10.3787/j.issn.1000-0976.2014.07.009
[38] POLIANNIKOV O V, MALCOLM A E, DJIKPESSEH, et al. Interferometric hydrofracture microseism localizationusing neighboring fracture[J]. Journal: Geophysics, 2011, 76(06): 1942-2156.
https://doi.org/10.1190/geo2010-0325.1
[39] URBANCIC T I, TRIFU C I, YOUNG R P. Microseismicityderived fault-planes and their relationship to focalmechanism, stress inversion, and geologic data[J]. GeophysicalResearch Letters, 2013, 20(22): 2475-2478.
https://doi.org/10.1029/93GL02937
[40] 陈海潮, 唐有彩, 钮凤林, 等. 利用微地震参数评估水力压裂改造效果研究进展[J]. 石油科学通报, 2016, 1(02): 198-208.
https://doi.org/10.3969/j.issn.2096-1693.2016.02.016
[41] COOKE M L. Fracture localization along faults withspatially varying friction[J]. Journal of GeophysicalResearch: Solid Earth, 1997, 102(B10): 22425-22434.
https://doi.org/10.1029/97JB01829
[42] ZHANG X, JEFFREY R G. Fluid-driven nucleation andpropagation of splay fractures from a permeable fault[J]. Journal of Geophysical Research: Solid Earth, 2016, 121(7): 5257-5277.
https://doi.org/10.1002/2015JB012546

Fast Inversion of Fracture Networks Created by Hydraulic Fracturing Treatment Using Transient Pressure History

LU Liangwu¹, LIU Wei², ZHANG Juncheng², ZHANG Xi^1,*, LI Zhi¹

(1. Faculty of Engineering, China University of Geosciences, Wuhan 430074, China
2. CNPC Chuanqing Drilling Engineering Company Limited, Chengdu 610051, China)

Abstract: As a critical component in the stimulation of unconventional oil and gas reservoirs, the accurate characterization of the spatial distribution of hydraulic fracture networks forms the basis for evaluating fracturing effectiveness and calculating hydrocarbon recovery. In this study, a coupled fluid-solid numerical model for hydraulic fracturing is employed to characterize the dynamic propagation behavior. of fracture networks, while simultaneously capturing the corresponding wellhead pressure responses. Based upon this, a Bayesian trans-dimensional inversion method is developed by integrating the Reversible Jump Markov Chain Monte Carlo (RJ-MCMC) algorithm with a parallel computing framework, enabling real-time inversion of fracture network geometry based on field injection pressure curves. In this approach, discrete fracture elements within the network—characterized by their geometric properties and spatial distribution— are treated as stochastic variables. Given the independence of fracture growth, random sampling is carried out in parallel across multiple threads. By combining the physical model with observational data, the Metropolis-Hastings- Green (MHG) criterion is applied to screen the sampling results, efficiently generating a set of fracture network samples that align with the measured wellhead pressure data. Subsequently, a Greedy Algorithm is applied to select the fracture geometry with the best pressure-matching accuracy as the inversion result and to optimize the fracture network parameters for the subsequent time step, thereby improving inversion efficiency. Finally, to verify the feasibility of the proposed method, pressure data from Stage 4 of Well H in a shale gas field in southwestern China were used to invert the fracture network geometry, and the results were compared with microseismic monitoring data. The comparison demonstrates strong consistency in both time and space between the fracture geometries derived from inversion and those from microseismic monitoring. Although aspects of the inversion method, such as pressure data selection, still require improvement, the proposed approach undoubtedly provides a novel solution for the real-time evaluation of fracture geometries during hydraulic fracturing operations.

Keywords: Hydraulic fracturing, trans-dimensional Bayesian inversion method, random propagation of fracture network, Markov Chain Monte Carlo(MCMC)

DOI: 10.48014/cpngr.20250417001

Citation: LU Liangwu, LIU Wei, ZHANG Juncheng, et al. Fast inversion of fracture networks created by hydraulic fracturing treatment using transient pressure history[J]. Chinese Petroleum and Natural Gas Research, 2025, 4(2): 23-40.