加卸载条件下岩石天然裂缝摩擦强度弱化机理的研究
(1. 中国地质大学 (武汉) 工程学院, 武汉 430074
2. 中国科学院武汉岩土力学研究所, 武汉 430071)
摘要: 含天然裂缝的岩石在周期加卸载条件下起裂压力会降低这一现象已被室内和矿场实验所证明, 裂缝面摩擦强度在周期荷载下弱化是其重要机理。本文建立了基于裂缝面颗粒材料剪切变形特征的微结构模型, 将裂缝面内颗粒所形成的力链等效为能承受压剪载荷的弹性杆, 并且力链在滑移方向改变时会重新组合成新的弹性杆; 通过对弹性杆变形和破坏的微结构力学分析, 研究了摩擦滑动启动、停止和反向滑动各阶段的力学特征, 建立相应的摩擦本构方程。研究结果表明: 滑移产生的弹性变形会降低裂缝面的摩擦强度, 具有滑移弱化摩擦本构的形式, 其本构参数由裂缝面颗粒材料的弹性性能决定; 滑移方向改变会引起额外能量损失, 产生摩擦系数跳跃。利用前人的断层泥摩擦实验结果确定了本构方程中各参数的取值范围, 并提出了它们与裂缝面摩擦材料物理性能之间的关系。本文通过研究微结构演化规律为揭示岩石强度在加卸载条件下弱化机理提供了一个新解释。
关键词: 岩石裂缝, 裂缝面摩擦, 加卸载, 微结构模型, 摩擦本构
DOI: 10.48014/cpngr.20250417002
引用格式: 高振朝, 杨建平, 张浠, 加卸载条件下岩石天然裂缝摩擦强度弱化机理的研究[J]. 中国石油天然气研究, 2025, 4(2): 10-22.
文章类型: 研究性论文
收稿日期: 2025-04-17
接收日期: 2025-04-24
出版日期: 2025-06-28
0 引言
在隧道掘进、油气、地热能源开采等地球浅部人类活动中岩石会承受周期性加卸载。在循环加卸载作用下，加载曲线和卸载曲线会形成非闭合的滞回圈，其面积表征了在循环载荷下岩石能量的耗散程度，同时岩石的承载能力也会随着滞回圈数目的增多而下降，产生所谓的弱化现象[1,2]。众所周知[3-6]，岩石内部存在大量的天然微裂缝，闭合裂缝摩擦特征是岩石强度弱化的根源之一，将直接造成地热储层压裂改造的起裂压力降低。即使岩石变形处于弹性阶段时，也可以观测到滞回圈。这证明即使裂缝不扩展，处于受压状态的裂缝面摩擦滑移也会在能量耗散方面作出贡献。因此研究岩石天然裂缝面在周期性荷载下摩擦强度弱化和耗能机制对岩石破坏极为重要。
Feeny等[7]总结了影响摩擦性能的诸多因素和摩擦本构方程的不同形式。Ida[8]和Palmer和Rice[9]提出了滑移弱化摩擦本构，定量给出了不稳定滑移萌生的摩擦耗能。Ruina[10]通过一维滑块模型提出著名的依赖速率-状态的唯象理论，并引入有效接触时间来描述滑移过程，认为在相对速度发生变化后，接触表面会形成滑移历史来记录滑移状态，从而改变摩擦系数。Uenishi和Rice[11]证明在某些情况下速率-状态定律可退化为滑移弱化本构。上述唯象摩擦本构能很好地描述滑移方向不变和不稳定滑移的地震现象，但针对天然裂缝的满缝长小滑移量，不断重复滑移方向改变且无裂缝扩展的情况，它们是否成立值得商榷。
目前涉及微裂缝摩擦本构的研究基本上采用库仑摩擦定律。David等[12]基于岩石中裂缝等长和均匀角度分布假设，研究了由库仑摩擦定律卸载和反向滑移启动条件决定的裂缝数目变化所产生的滞回圈现象。但其模型无法解释在给定最大载荷下岩石承载能力随循环次数增加而下降和滞回圈面积增大的观测结果。为了得到裂缝面在加卸载时的力学行为，需要了解滑移过程所涉及的物理过程，如摩擦面介质颗粒运动[13-15]和表面粗糙产生的接触[16-18]。这些裂缝间介质的变形往往具有整体力学性质[19]。因此，利用微结构力学模型研究裂缝间介质的弹性变形能力可能对解释裂缝面在循环加载下的摩擦本构更加直接有效[20]。
本文将建立在加卸载条件下裂缝面摩擦本构关系，进一步说明含天然裂缝岩石(包括页岩)的强度弱化来源于材料内在的摩擦特征。首先，基于裂缝面上由颗粒形成具有弹性变形能力的力链假设，建立关于裂缝面摩擦滑移的微结构模型。然后建立加卸载过程摩擦滑动启动、停止、反滑启动的各个物理过程的本构方程，揭示滞回圈特征及能量耗散机制。最后，将分析数值结果的物理意义和给出确定摩擦本构中力学和摩擦面几何参数的方法。
1 模型建立
1.1 模型假设
假设1:岩石基体处于弹性变形阶段，天然裂缝面闭合并经历摩擦滑动，同时摩擦面由一定厚度的颗粒材料组成。在摩擦滑移过程中，若滑移面长度大于临界尺度，滑移区将迅速增大[11]。
假设2:闭合裂纹面滑移区尺度较小且不变，滑移过程中不存在所谓“裂缝”形式，即不产生以动摩擦为主的能量耗散。
假设3:定义摩擦系数μ=Q/P。在滑移过程中，岩石天然裂缝中含有因磨损而产生颗粒介质，颗粒间的相互作用(接触蠕变和摩擦)会对裂缝摩擦带来影响。Mair等[21]通过观察实验后的微结构形态，确定了颗粒力学行为和裂缝面摩擦之间的相关性。对于表面粗糙的裂缝面上相互接触的微凸体也可以用弹性变形来表征摩擦特征[16]。同样地，将裂缝面内颗粒的集合等效为在上下岩石之间的弹性块体，厚度为l，块体在受到由岩石施加的恒定法向力P，和变化剪切力Q作用下发生稳态剪切变形，如图1b所示，因此可以定义摩擦系数μ=Q/P，同时在模型中上下岩石被视为弹性体(图1a)。
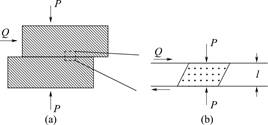
图1 裂缝面颗粒介质的弹性体假设
Fig.1 Assumed elasticity of granular materials on fracture surface
1.2 力链结构
将弹性块体看作多个力链的组合体[22](图2a)，在变形过程中，每个力链会受到相邻力链传递的法向力和剪切力的反力。颗粒会自行组合形成多力链集合(图2b黑色虚框内)以保持力的平衡状态。假设独立受力的多力链集合组成了具有相同宽度h的介质微元E(图2c黑色虚框内)，多力链集合被贯通裂缝所隔离，因此不产生相互作用。并且在滑移过程中，这些力链会保持相当稳定[23]。
Morgan[22]在颗粒动力学模拟中，发现力链变形运动与鬃毛模型类似，区别在于力链变形更接近两端固定的弹性杆压弯变形，其宏观摩擦力由弹性杆刚度产生，因此本文通过两端固定的可压弯弹性杆来描述裂缝面上多力链集合的受力过程(图3)。杆宽度由低于毫米量级的
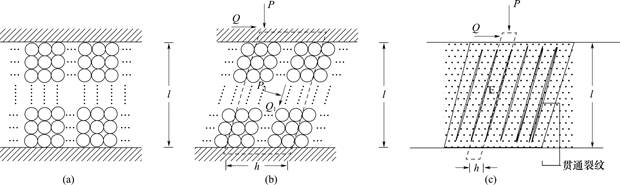
图2 力链模型
Fig.2 Force chain model(representative volume element)
颗粒尺寸决定，在长度方向上存在多个颗粒接触生成力链，因此杆的剪切应变不计。对弹性杆建立坐标系，以杆下支座中点为原点，轴向为x方向，横向为z方向;下支座全约束，上支座只约束转动;根据微结构几何，设杆长为l，宽为h，其纵向厚度设为1;受外力作用下支座x方向位移为λ，剪切滑移过程极缓慢，不考虑速度的影响，为准静止变形过程。
另外，摩擦滑移面前沿的不断扩展会对已变形的弹性杆产生干扰，使其所受的剪力达到新的摩擦强度。在本模型中，假设由于杆内某处受力已达到许可拉应力[σ]，出现稳态弹性变形失效，造成摩擦滑移启动。在后续滑移过程中，系统能量通过滑移弱化行为降低(图4)，损耗的能量G称为表观断裂能[24]，组成杆件的颗粒数目和力链结构不变[23]，能量耗散归因于颗粒旋转。因此，摩擦滑移被看作由于杆的弹性变形造成的材料失效过程。
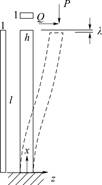
图3 弹性杆变形
Fig.3 Deformation of elastic rods
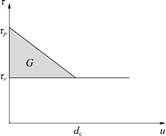
图4 表观断裂能
Fig.4 Apparent fracture energy
2 滑移阶段
2.1 弹性杆变形
为了推导简便，基于对称性将杆延长至2l(图5a)，弹性杆在压力P作用下产生竖向位移2λ，剪力Q作用下产生中点挠度a。其下端局部如图5b所示，杆在外力作用下，发生压缩和弯曲双重变形，在杆的横截面上(虚点线)将发生角度为θ的偏转。由材料力学简单分析可知下端产生局部最大拉应力。
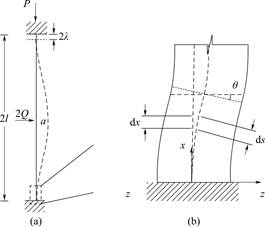
图5 杆固定端附近局部变形图
Fig.5 Local deformation near the fixed end of the rod
根据线性叠加原理，在x方向上的位移，应变和应力场为(附录A):
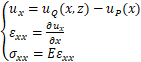(1)
式中，uQ(x)是2Q作用下x方向的位移，uP(x)是P作用下x方向的位移，E是颗粒介质的弹性模量(MPa)。
以三角级数的形式(附录A)表示挠度曲线并适用于杆的全长。在本文中，取级数的第一项进行计算:
w(x)=asin2
(2)
式中，a是待定系数，表示杆中点的挠度(裂纹面相对位移)。挠度曲线满足一阶导数在两端均等于零的边界条件。
同时得到λ与a的关系(附录A):
λ(a)=
+εl(3)
式中，ε是P作用下轴向压应变。
2.2 临界位移
杆在Q作用下产生临界位移(挠度)时，承受的应力将超过[σ]，会产生断裂失效。此时杆中点处的最大挠度为acr。由于最大拉应力发生在固定端点处(x=0)。将挠曲线方程代入式(1)，得到杆下端横截面的应力表达式:
σx=0=-Ez
-
(4)
将z=-h/2代入上式，为避免杆断裂失稳，需满足
≤[σ]，则临界位移acr为:
a≤
=acr(5)
式中，有效许可拉应变[ε]eff=[σ]eff/E=([σ]+P/h)/E。
2.3 初始摩擦系数
不同于弹性杆的受力分析，摩擦滑动本身是一个单边约束结构的稳定性问题。当杆在某时刻的变形已知时，将对杆的运动产生扰动，当杆内出现材料破坏失稳时，则滑移开启。通过分析弹性杆临界状态得到摩擦系数在不同滑移量下的演化关系。
弹性杆的稳定性分析是基于能量方法，如附录B。同时假设各弹性杆之间无相互作用和能量传递。如图6所示，当弹性杆初始无变形，即滑移位移为零，弹性杆破坏将经历从无变形到临界挠度acr的能量变化。由此可得到初始摩擦系数(图6左边箭头长实线)。同样地，在某一滑移位移us时，杆已具有最大挠度us，从挠度us到临界挠度acr的能量变化将给出该状态下的摩擦系数(图6右边箭头短实线)。由不同滑移量的摩擦系数可以得到摩擦系数随滑移量的变化曲线(图6中虚线)。当曲线是线性时，将给出斜率ks;称之为弱化速率。
图6 加载时的滑移弱化包络线
Fig.6 Slip-weakening envelope during loading
不同滑移量下的摩擦系数由能量守恒给出。初始摩擦系数为(详见附录B.1):
=
(6)
2.4 滑动阶段摩擦系数
当裂缝面开始滑移后，力链内颗粒之间存在相对转动，产生能量变化。假设力链内颗粒相互接触关系并没有改变，因此转动产生的能量仍储存在弹性杆中。局部转动可以在Morgan[22]的颗粒动力学模拟结果中看到。而且杆表面的变形保持了弹性杆之间在边界上的位移连续，使杆内材料恢复到弹性状态，因此杆的破坏仍需要达到临界位移条件。当然对处于某一滑移位移us的变形杆，都可采用上述计算方法获得摩擦系数。
根据能量守恒，外力做功等于应变能的变化量，得到摩擦系数线性弱化包络线方程(附录B.2):
μs
=-
us(7)
式中，us表示杆中点处的滑移量。
上述模型完全还原了滑移弱化本构，除此之外，还可以看到经典滑移弱化曲线与本文模型曲线的区别(图7)。经典滑移弱化本构认为经过特征滑移量Dc后，摩擦系数弱化到一定程度，继续滑移会保持在某一特定残余值。然而，动摩擦系数情况不在本文模型讨论的范围内，认为滑移永远处于“屈服”阶段，不产生所谓“裂缝”形式的不稳定滑移。
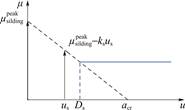
图7 经典滑移弱化包络线
Fig.7 Classic slip-weakening envelope
3 滑移方向改变
3.1 反滑启动摩擦系数
在岩石内部，假设微裂纹尺寸极小，正向滑移量小于临界位移，并且正向滑移→滑移停止→反向滑移启动是快速完成的，少量能量使力链重构，产生新的弹性杆。不同于初始滑移，反滑开始时，杆已具有一定的能量。因此，在构建反向滑移的摩擦物理模型时，假设摩擦面在加载后已产生正向滑移量b(图8)。
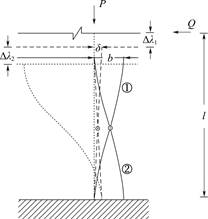
图8 卸载时裂缝弹性杆的滑移模型(1代表旧杆，2代表新杆)
Fig.8 Slip model of fracture elastic rod during unloading(1:old rods;2:new rods)
在反向滑移启动的瞬间，弹性能使双杆突变成具有残余变形δ(0<δ<b)的另一中间过渡态(虚段线)，并将其作为后续滑移的初始状态;随着摩擦面反向滑移，旧杆恢复成直杆，并和铰一起消失;双杆系统又恢复为单杆系统，继续滑移，直至新杆达到临界破坏状态(虚点线)。反滑过程中杆的变形分析与前面一致。
基于能量守恒方程和杆破坏准则，得到滑移方向改变瞬间的反滑启动摩擦系数(附录C.1):
=
(8)
式中，δ表示杆滑移方向改变瞬间残余滑移量。
3.2 反向滑动阶段摩擦系数
滑移方向改变后的摩擦本构推导过程与正向滑移类似(附录C.2)。任意反向位移ur下的摩擦系数为:
μr
=-
ur(9)
式中，ur表示反向滑移时杆中点挠度。
首先，对滑移和反滑阶段的摩擦本构进行无量纲处理，得到:
μs
=β-βns(10)
μr
=
-β
nr(11)
式中，β=l[ε]eff/2h表示弹性体的抗剪能力，ns=us/acr表示加载滑动时的无量纲裂缝面滑移，nr=ur/acr表示卸载反向滑动时的无量纲裂缝面滑移，
=δ/acr表示卸载开始无量纲残余滑移，表征反向滑移启动开始时摩擦面状态的变化。必须注意的是，滑移弱化摩擦本构中的弱化速率由β/acr给出。
4 结果分析和讨论
4.1 无量纲参数
加卸载下摩擦本构中有两个无量纲参数β、和临界位移acr。与前人的摩擦实验结果比较，可以给出它们的物理含义和取值范围。滑动起始的静摩擦系数β在许多断层泥摩擦实验[25-27]中已经测出在0.6~0.8之间。与Ruina[10]在速率-状态本构中引入的状态变量类似，表征反向滑移启动开始时由正滑和滑移停止造成的摩擦面状态变化。然而Ruina[10]在引入θ时并没有赋予该变量物理含义，而在本模型中则具体表示弹性杆在反向滑移前所具有的残余变形量。acr与滑移弱化本构中的Dc具有相似的物理含义，即剪应力弱化的临界滑移距离，其值随着摩擦面介质弹性的几何尺寸即断层泥厚度变化而变化，从现场地震资料中推断Dc值在1~10m量级，而在低滑移速度下的实验室测量得出的数值更小，在0.01~1mm之间。必须注意的是，滑移弱化本构中Dc是剪应力弱化到残余水平时的滑移量，而在本模型中当滑移距离达到acr时则弱化到零，两者虽处于同一量级，但却有一定的差值，因此，acr的物理意义可表示为当介质弹性完全丧失抗剪能力时的滑移量。
4.2 摩擦系数跳跃
Scuderi等[23]实验结果表明，一旦颗粒材料内力链在开始滑移过程形成，其在后续的恒速滑动过程中具有基本不变性。因此，当正向和反向恒速滑移时，可以不考虑裂缝面状态的改变。在上述摩擦本构推导中并没有考虑滑移速度的影响，换句话说，在上面滑移摩擦本构中已隐含恒速的假定。在与变速摩擦实验结果比较时，模型从正向到反向滑移经历了速度变化，其本质相当于速度步进的一个极限情况，因此应该具备变速摩擦滑动的基本特征，譬如，摩擦系数跳跃现象。
在速度步进摩擦实验中，滑移面滑移速度的增加导致摩擦系数的突变[28]。从微观上分析是由于断层泥发生“固结”强化[26]，即纳米颗粒重新排列变得更紧密，往往需要更大的剪力使断层泥发生变形。这一微观分析表明滑移方向改变也会产生颗粒重新排列。在滑移方向改变时，重新排列的颗粒使裂缝面“固结”强化，其组成的力链也发生结构变化。在摩擦本构中也看到改变滑移方向需要对断层泥系统输入更多的能量，和实验结果具有相同的物理机制。因此，考虑裂缝面在卸载后再改变滑移方向的过程，是变速滑动实验的一种极端情况。与滑移方向改变造成的颗粒重新排列形成新力链所需要的能量有关联。其摩擦系数突变量计算公式如下:
Δμ=βns-
(12)
4.3 acr和
(1)临界位移acr
断层泥摩擦实验结果常常被用来估算摩擦本构参数。在低正应力下的滑移弱化过程，Marone[25]和Nakatani[26]针对花岗岩间断层泥，利用双剪装置中在不同正压力下开展了滑移弱化关系的评估。结果表明，除去加载段和稳滑段，摩擦滑移弱化的过程近似于线性，在低正压力(1MPa<σn<4MPa)，β=0.6~0.7，Δμ≈0.035，Dc≈30μm，弱化斜率ks=Δμ/Dc≈1.17/mm，由此可知滑移弱化的距离与临界滑移距离之比acr/Dc=β/Δμ≈17~20;在一般正压力(5MPa<σn<25MPa)，Δμ≈0.02~0.08，Dc≈0.1-1mm，弱化斜率ks=Δμ/Dc≈0.08~0.2/mm，acr/Dc=β/Δμ≈8~54。Rice[29]和Wong[30]对完整花岗岩试件在不同围压下的实验室剪切断裂测试进行了滑移弱化关系和剪切断裂能的评估，结果表明，正压力在(60MPa<σn<140MPa)范围内，滑移弱化的距离Dc≈440μm，Δμ≈0.16~0.3，弱化斜率ks=Δμ/Dc≈0.36~0.7/mm，acr/Dc≈2.3~4.3。图9给出了利用这些实验结果计算得到的acr，可以看到:当岩石中裂缝在地壳中埋藏越深，受到的正压力越大，由微结构模型得到的acr与实验获得Dc的结果越接近。
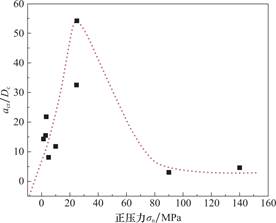
图9 不同正应力下模型和实验参数
Fig.9 Comparison of model and experimental parameters under varying normal stresses
Brantut等[31]计算表明，关系式Dc∝1/
成立，其中σn是裂缝面的正应力，可推断出的Dc值范围从法向应力为10MPa的几毫米到100MPa的几百微米。因为断层泥的厚度与它所受的正压力成反比[32]，并在较大正压力作用下，断层泥有应变硬化，即在较大正压力作用下，断层泥的厚度减少。方程(5)也可推断acr随正应力变化，acr与断层泥厚度l的平方成正比，推得
∝1/P2(其中P为正压力)，得到与Brantut等一致的计算结果。
Cocco和Bizzarri[33]发现自然地震的Dc比实验室的结果大一个量级可能是由于高滑移速度造成的。本文研究对象是循环载荷下的岩石内部裂纹，并认为其摩擦行为受滑移弱化摩擦本构控制，岩石积累的弹性能在裂纹释放，使裂纹面摩擦滑移速度远大于Deterich和Okubo[24,27]、Marone[25]和Nakatani[26]的实验情况，且acr的估算结果同样比Dc普遍大一个数量级。因此，本文acr的估算结果可能更适合循环载荷下的摩擦行为。即使如此，也不能完全消除滑移弱化摩擦本构的应用价值，譬如，在滑移速度较大时，摩擦本构呈现速度无关性[11]。
(2)残余变形
在式(12)中可以看出，摩擦系数在改变滑移方向时的突变量是关于抗剪强度β、正向停止时的滑移量ns和无量纲残余位移的函数。在速率状态本构中，速度增加倍数控制着摩擦系数跳跃中的突变量，状态变量则控制着跳跃后摩擦演化行为。在本模型中，不仅影响着突变量，还与跳跃后的弱化速率有关，因此可以根据式(12)利用速度切换结果中的摩擦系数跳跃和变化后的弱化速率来计算残余变形参数。
这里采用目前广泛接受的变速摩擦实验结果来估算残余变形。Deterich和Kilgore[27,28]、Marone[25,34]针对花岗岩间断层泥开展了低正压力下(5MPa<σn<25MPa)速度依赖性的评估。实验中速度切换一般以10倍为步进阶梯，滑移弱化过程同样被视作线性。以ns=0.5为例，在(0.4μm/s→4μm/s)速度切换中，Δμ≈0.01，滑移弱化距离Dc≈0.03mm，=(
-1)/5≈0.28358;在(1μm/s→10μm/s)速度切换中，Δμ≈0.015，Dc≈0.1mm，≈0.28038;在(2.5μm/s→25μm/s)速度切换中，Δμ≈0.0175，Dc≈0.1mm，≈0.27878。在不同ns的结果见图10。
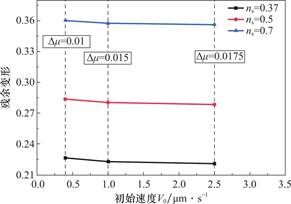
图10 初始速度和残余变形关系曲线
Fig.10 Relationship between initial velocity and residual deformation
由于实验滑移速度较小，表现出对速率的低敏感性，主要由正向滑移停止时的滑移量决定(即滑移历史)。在本模型中，表示在循环载荷下的正滑结束，反滑开始的低速阶段的残余变形，从能量角度分析，主要取决于摩擦系统在反滑开始时的能量。与图10的实验条件较为一致。当正向滑移量增大，储存在摩擦滑移区内的能量变大，用于反滑启动的弹性能则减小，相应的值也越大。
4.4 微结构参数
在模型中，无量纲参数表示摩擦启动时的初始摩擦系数，在实验结果中容易确定。同时该变量也有明确的微结构力学含义，即依赖于弹性杆的力学性能和几何参数。β=[ε]effl/2h由两部分组成:颗粒介质弹性表征量[ε]eff=([σ]+P/h)/E和弹性体几何表征量l/h。其中l在摩擦实验中表示断层泥的厚度，h正比于断层泥颗粒尺寸，通常情况下l与h的比值约为5。P表示正压力，许可拉应力值和正压力P相比，可忽略不计。这些物理量可以通过断层泥的力学实验获得，包括介质弹性模量E。因此，在对断层泥进行力学性能和几何上的测试后，可以确定初始摩擦系数的大小。这也为确定摩擦本构提供了另一个途径。
微结构参数本质上是为了表征滑移区颗粒材料的几何和物理特性，在微观研究层面上，岩石材料的物理特性不是本文的研究重点，本文聚焦于滑移区的层间介质颗粒运动。滑移区的颗粒运动(平动和转动)和相互作用(接触蠕变和摩擦)难以用一个全面的物理模型表征，适当的简化是必需的，本文在构建模型时提出杆模型的许可拉应力表征抗剪能力这一假设，形式简洁但可能并不能完全满足实际应用中的情况，在应用到具体实际问题中需要更多物理量来参与分析描述。
5 结论
本文从研究岩石内部裂缝的摩擦本构出发，根据裂缝面堆积颗粒介质的运动特点，构建了以弹性杆为研究对象的摩擦物理模型;并基于能量守恒定律和许可拉应力判别准则，推导了加卸载条件下摩擦本构方程和其参数表达式;最后利用经典摩擦实验结果对参数进行估算，得到了较好的结果。结论如下:
(1)本文提出的微结构力学模型可以用来推导循环载荷下摩擦本构。首先还原了被广泛接受和应用的滑移弱化摩擦本构关系;其次也还原了卸载时滑移方向改变瞬间摩擦系数跳跃现象。
(2)从摩擦面颗粒材料的弹性参数来决定摩擦本构参数，可以为实验给出的唯象摩擦本构赋予清晰的物理含义，如无量纲参数β表征了介质碎屑颗粒的抗剪能力，而可以用来描述改变摩擦面状态对摩擦系数的影响。
(3)在理论摩擦本构与实验数据进行拟合中，临界位移acr在高正应力和低中滑移速度下更接近实验Dc值，该摩擦本构更适用于深埋的含裂缝岩体在工程条件下的摩擦特征;无量纲残余变形对速率表现出低敏感性。
由于岩石裂缝面的摩擦性能存在的空间不均匀性，即使对于加卸载下弹性阶段岩石能量耗散来源，理论和实验研究仍存在一定的困难。本文从微结构弹性变形给出裂缝面颗粒材料弹性性能参数与摩擦本构参数的关系。微结构力学模型应该能更清晰反映加卸载条件下的裂缝面摩擦强度弱化的内在特征。
利益冲突: 作者声明没有利益冲突。
附录:
A 弹性杆位移，应变和应力
对于图4所示弹性杆系统，由于位移只是x的函数，设杆沿x方向的位移为ux(x)，和沿z方向的位移为挠曲线w(x)。故杆内x方向位移场为:
ux
=-zθ-∫
-
(A1)
式中θ表示杆横截面偏转角度(弧度);ds表示挠曲线微段;dx表示相应的弦微段;A表示杆横截面面积。
运用欧拉梁理论得到杆x方向应变:
εxx=-z
w(x)-
-
(A2)
利用线弹性本构可以计算杆x方向的应力:
σxx=-Ezw(x)-
-(A3)
以满足端点条件的三角级数表示挠度曲线。在两端固定的情况下，挠度曲线可以表示为:
w(x)=
ansin2
(A4)
式中a1=a。在本文中，n=1。具体表达式见方程(2)。
在法向力P作用下杆轴向长度l'为:
l'=2l
(A5)
式中ε=
。同时设杆轴向长度变化量为2λ。利用挠度曲线，也可以求得当前杆轴向长度l':
l'=
ds=
dx=
E(m)(A6)
式中m=-[πa/2(l-λ)]2，E(m)为椭圆积分曲线。
由变形后杆轴向长度相等可得:
2l=E(m)(A7)
式中椭圆积分曲线渐进展开为:
E(m)=
-
(A8)
若取一阶近似得到支座x方向位移:
λ=
+εl(A9)
假设λ远小于l，上式简化为:
λ=+εl(A10)
B 滑移弱化摩擦本构
B.1 初始摩擦系数
摩擦本构的推导是基于能量法，杆件同时受到剪切力和法向力P做的功。杆的内能表达式包括轴向压缩应变能和弯曲应变能的表达式:
U=
ε2dx+
dx(B1)
将挠度曲线代入上式并积分得到杆最大挠度为a时的应变能:
U(a)=
+
(B2)
杆件法向力P和剪切力Q所做的功之和:
WP+Q(a)=
P·2λ+·2Qw(l-λ)
=Pλ+Qa (B3)
假设杆最大扰度达到临界位移acr时，杆将发生破坏。由方程(A10)可得到相应的支座位移的临界值λcr。若杆在破坏前无能量，根据能量守恒定律:
WP+Q
=U(B4)
可得:
Pλcr+Qacr=
+
(B5)
运用泰勒公式展开上式右边第二项，可以得到:
=
+
-
(B6)
因此初始摩擦系数为:
=
=
-
(B7)
由于[ε]eff与e具有相同的量级，略去e的高阶项后，得到:
=(B8)
B.2 滑移阶段的摩擦系数
在滑移阶段，杆件已具有最大挠度为us的扰度曲线。假定在施加外力后，挠度会继续增大直到杆件破坏。因此滑移产生的扰度曲线和后续破坏产生的扰度曲线分别为:
(B9)
式中w表示滑移产生的挠度曲线;w'表示后续破坏产生的挠度曲线;Δλ表示支座x方向位移变化量:
Δλ=
+εl-
(B10)
因此滑移产生的应变能和后续破坏产生的应变能为:
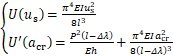(B11)
根据能量守恒定律
WP+Q+U=U'(B12)
可建立下列方程:
PΔλ+Qacr+
=
+
(B13)
由上式可得到滑移阶段的摩擦系数:
μs=
=-
-
us-
(B14)
略去e的高阶项后得到:
μs==-us(B15)
C 滑移方向的影响
C.1 反滑启动摩擦系数
在滑动停止时，弹性介质内存在二个弹性杆。它们的滑移量或最大扰度为d。经历短暂时后反滑启动，介质内只存在一个杆。①杆和②杆滑动停止时的挠度曲线和反滑启动时产生破坏的挠度曲线分别为:
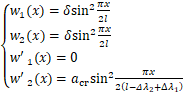(C1)
式中w1和w2表示双杆系统初始时①杆和②杆挠度曲线;w'1和w'2表示双杆系统临界状态时①杆和②杆挠度曲线;Δλ1和Δλ2表示①杆和②杆支座x方向位移变化量:
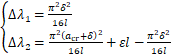(C2)
因此，对于二个杆，在滑动停止时和后续破坏产生的应变能为:
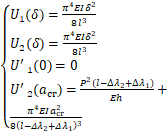(C3)
根据能量守恒定律，
WP+Q+U1(δ)+U2(δ)=U2'(C4)
可得:
P
+Qacr+
=
+
(C5)
将方程(C2)代入上式，化简后可得反滑启动摩擦系数:
=
-
-
(C6)
略去e的高阶项后得到:
=
(C7)
C.2 反滑阶段摩擦系数
仍然沿用C.1的方法计算反滑阶段摩擦系数。考虑到反滑产生的滑移量，①杆和②杆滑动停止时的挠度曲线和反滑启动时产生破坏的挠度曲线分别为:
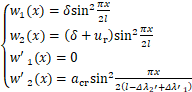(C8)
式中ur表示滑移方向改变后的位移;Δλ'1和Δλ'2表示反向滑移ur时①杆和②杆支座x方向位移变化量:
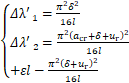(C9)
根据能量守恒定律:
WP+Q+U1(δ)+U2
=U'2(C10)
可得:
PΔλ'+Qacr+
=
+
(C11)
简化后得到反滑阶段摩擦系数:
μr=-
-
-
ur
-
(C12)
略去e的高阶项后得到:
μr=
-ur (C13)
利益冲突: 作者声明无利益冲突。
[①] *通讯作者 Corresponding author:张浠，zhangxi@cug.edu.cn
收稿日期:2025-04-17; 录用日期:2025-04-24; 发表日期:2025-06-28
基金项目:本项研究得到了国家自然科学基金项目(资助号42277184)资助。
参考文献(References)
[1] Zang, A, Yoon, J. S. , Stephansson, O. , Heidbach, O. Fatigue hydraulic fracturing by cyclic reservoir treatment enhances permeability and reduces induced seismicity[J], Geophysical Journal International, Volume 195, Issue 2, November, 2013, Pages 1282-1287,
https://doi.org/10.1093/gji/ggt301.
[2] Gong F, Yan J, Wang Y, et al. Experimental study on energy evolution and storage performances of rock material under uniaxial cyclic compression[J]. Shock and Vibration, 2020, 2020: 1-14.
https://doi.org/10.1155/2020/8842863.
[3] Walsh J B. The effect of cracks on the uniaxial elastic compression of rocks[J]. Journal of Geophysical Research, 1965, 70(2): 399-411.
https://doi.org/10.1029/JZ070i002p00399.
[4] Kachanov M L. A microcrack model of rock inelasticity part I: Frictional sliding on microcracks[J]. Mechanics of Materials, 1982, 1(1): 19-27.
https://doi.org/10.1016/0167-6636(82)90021-7.
[5] Horii H, Nemat-Nasser S. Overall moduli of solids with microcracks: load-induced anisotropy[J]. Journal of the Mechanics and Physics of Solids, 1983, 31(2): 155-171.
https://doi.org/10.1016/0022-5096(83)90048-0.
[6] Lawn B R, Marshall D B. Nonlinear stress-strain curves for solids containing closed cracks with friction[J]. Journal of the Mechanics and Physics of Solids, 1998, 46(1): 85-113.
https://doi.org/10.1016/S0022-5096(97)00036-7.
[7] Feeny B, Guran A, Hinrichs N, et al. A historical review on dry friction and stick-slip phenomena[J]. Applied Mechanics Reviews, 1998, 51(5): 321-341.
https://doi.org/10.1115/1.3099008.
[8] Ida Y. Cohesive force across the tip of a longitudinal-shear crack and Griffiths specific surface energy[J]. Journal of Geophysical Research, 1972, 77(20): 3796-3805.
https://doi.org/10.1029/JB077i020p03796.
[9] Palmer A C, Rice J R. The growth of slip surfaces in the progressive failure of over-consolidated clay[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1973, 332(1591): 527-548.
https://doi.org/10.1098/rspa.1973.0040.
[10] Ruina A. Slip instability and state variable friction laws[J]. Journal of Geophysical Research: Solid Earth, 1983, 88(B12): 10359-10370.
https://doi.org/10.1029/JB088iB12p10359
[11] Uenishi K, Rice J R. Universal nucleation length for slip-weakening rupture instability under nonuniform fault loading[J]. Journal of Geophysical Research: Solid Earth, 2003, 108(B1).
https://doi.org/10.1029/2001JB001681.
[12] David E C, Brantut N, Schubnel A, et al. Sliding crack model for nonlinearity and hysteresis in the uniaxial stress-strain curve of rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2012, 52: 9-17.
https://doi.org/10.1016/j.ijrmms.2012.02.001.
[13] Cates M E, Wittmer J P, Bouchaud J P, et al. Jamming, force chains, and fragile matter[J]. Physical review letters, 1998, 81(9): 1841.
https://doi.org/10.1103/PhysRevLett.81.1841.
[14] Peters J F, Muthuswamy M, Wibowo J, et al. Characterization of force chains in granular material[J]. Physical review E, 2005, 72(4): 041307.
https://doi.org/10.1103/PhysRevE.72.041307.
[15] Zhang X, Jeffrey G R, Mai Y. A micromechanics-based Cosserat-type model for dense particulate solids[J]. ZAMP: Zeitschrift fur Angewandte Mathematik und Physik, 2006, 57(4): 682-707.
https://doi:10.1007/s00033-005-0025-6
[16] Greenwood J A, Williamson J B P. Contact of nominally flat surfaces[J]. Proceedings of the royal society of London. Series A. Mathematical and physical sciences, 1966, 295(1442): 300-319.
https://doi.org/10.1098/rspa.1966.0242.
[17] Yamada K, Takeda N, Kagami J, et al. Mechanisms of elastic contact and friction between rough surfaces[J]. Wear, 1978, 48(1): 15-34.
https://doi.org/10.1016/0043-1648(78)90135-7.
[18] Biegel R L, Wang W, Scholz C H, et al. Micromechanics of rock friction 1. Effects of surface roughness on initial friction and slip hardening in westerly granite[J]. Journal of Geophysical Research: Solid Earth, 1992, 97(B6): 8951-8964.
https://doi.org/10.1029/92JB00042.
[19] Bouchbinder, E. , E. A. Brener, I. Barel, and M. Urbakh, Slow cracklike dynamics at the onset of frictional sliding[ J]. 2011, Phys. Rev. Lett. 107, 235501.
https://doi.org/10.1103/PhysRevLett.107.235501
[20] 李国琛, 耶纳. 塑性大应变微结构力学[M]. 北京: 科学 出版社, 2003.
[21] Mair K, Frye K M, Marone C. Influence of grain characteristics on the friction of granular shear zones[J]. Journal of Geophysical Research: Solid Earth, 2002, 107(B10): ECV 4-1-ECV 4-9.
https://doi.org/10.1029/2001JB000516.
[22] Morgan J K. Particle dynamics simulations of rate-and state-dependent frictional sliding of granular fault gouge[J]. Computational earthquake science part I, 2004: 1877-1891.
https://doi.org/10.1007/s00024-004-2537-y.
[23] Scuderi M M, Collettini C, Viti C, et al. Evolution of shear fabric in granular fault gouge from stable sliding to stick slip and implications for fault slip mode[J]. Geology, 2017, 45(8): 731-734.
https://doi.org/10.1130/G39033.1.
[24] Okubo P G, Dieterich J H. Effects of physical fault properties on frictional instabilities produced on simulated faults[J]. Journal of Geophysical Research: Solid Earth, 1984, 89(B7): 5817-5827.
https://doi.org/10.1029/JB089iB07p05817
[25] Marone C. On the rate of frictional healing and the constitutive law for time-and slip-dependent friction[J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(4): 187.
https://doi.org/10.1016/S1365-1609(97)00054-3.
[26] Nakatani M. A new mechanism of slip weakening and strength recovery of friction associated with the mechanical consolidation of gouge[J]. Journal of Geophysical Research Solid Earth, 1998, 103(B11): 27239-27256.
https://doi.org/10.1029/98JB02639.
[27] Dieterich J H. Constitutive properties of faults with simulated gouge[J]. Mechanical behavior of crustal rocks: the Handin volume, 1981, 24: 103-120.
https://doi.org/10.1029/GM024p0103.
[28] Dieterich J H, Kilgore B D. Direct observation of frictional contacts: New insights for sliding memory effects [J]. Pure and Applied Geophysics, 1994, 143(1): 283-302.
https://doi.org/10.1007/bf00874332
[29] Rice J R. The mechanics of earthquake rupture[M]. Providence: Division of Engineering, Brown University, 1979.
[30] Wong T F. On the normal stress dependence of theshear fracture energy[J]. Earthquake source mechanics, 1986, 37: 1-11.
https://doi.org/10.1029/GM037p0001
[31] Brantut N, Schubnel A, Rouzaud J N, et al. High-velocityfrictional properties of a clay-bearing fault gouge andimplications for earthquake mechanics[J]. Journal ofGeophysical Research: Solid Earth, 2008, 113(B10).
https://doi.org/10.1029/2007JB005551
[32] Hirakawa E, Ma S. Dynamic fault weakening andstrengthening by gouge compaction and dilatancy in afluid-saturated fault zone[J]. Journal of GeophysicalResearch: Solid Earth, 2016, 121(8): 5988-6008.
https://doi.org/10.1002/2015JB012509.
[33] Cocco M, Bizzarri M. On the slip-weakening behavior ofrate-and state dependent constitutive laws[J]. GeophysicalResearch Letters, 2002, 29(11): 157-162.
https://doi.org/10.1029/2001GL013999
[34] Marone C. Laboratory-derived friction laws and theirapplication to seismic faulting[J]. Annual Review ofEarth and Planetary Sciences, 1998, 26(1): 643-696.
https://doi.org/10.1146/annurev.earth.26.1.64
Mechanism of Frictional Strength Degradation of Natural Rock Fractures under Cyclic Loading and Unloading
(1. Faculty of Engineering, China University of Geosciences, Wuhan 430074, China
2. Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, Wuhan, 430071, China)
Abstract: Laboratory and field experiments have demonstrated that the breakdown pressure of rock containing natural fractures decreases under cyclic loading and unloading, yet the underlying mechanism remains insufficiently understood. This paper studies the weakening mechanism of fracture surface frictional strength under cyclic loading through microstructural mechanical analysis, aiming to elucidate the failure process of naturally fractured rock. A microstructure model is developed based on the shear deformation behavior. of granular materials on fracture surfaces, in which particle-formed force chains are idealized as elastic rods capable of bearing combined compressive and shearing loads. The model further assumes that when the shear direction reverses, the force chains reorganize into new elastic rods. By analyzing the deformation and failure mechanics of these elastic rods, the study systematically explores the mechanical behavior. during slip initiation, arrest, and reversal, and derives corresponding frictional constitutive equations for each stage. The results indicate that slip-induced elastic deformation leads to a reduction in the apparent frictional strength of fracture surfaces, which is governed by the elastic properties of the granular materials. Reversal of slip direction results in additional energy dissipation and causes sudden fluctuations in the friction coefficient. By aligning with the phenomenological slip-weakening friction law, the model parameters are constrained through calibration against existing experimental data on fault gouge friction. This microstructural approach provides a novel framework for understanding the weakening mechanisms of rocks subjected to cyclic loading and unloading
Keywords: Rock fractures, fracture surfaces friction, cyclic loading and unloading, microstructure model, frictional constitutive law
DOI: 10.48014/cpngr.20250417002
Citation: GAO Zhenchao, YANG Jianping, ZHANG Xi. Mechanism of frictional strength degradation of natural rock fractures under cyclic loading and unloading[J]. Chinese Petroleum and Natural Gas Research, 2025, 4(2): 10-22.