预应力型钢混凝土框架恢复力特性研究
(1. 扬州市市政设施管理中心, 扬州 225000
2. 扬州大学建筑科学与工程学院, 扬州 225000)
摘要: 在合理选用材料本构模型的基础上, 分别使用ABAQUS和OpenSEES有限元软件, 构建了单榀预应力型钢混凝土框架数值模型, 并进行了单调和滞回受力全过程数值分析, 分析了该类型框架结构的滞回特征。通过参数分析, 确定了影响此类框架滞回特性的主要参数, 并由此建立了恢复力模型。研究结果显示: 通过ABAQUS软件构建的数值模型可以直观反映框架的破坏形态和应力分布, 模拟峰值荷载为191kN, 与试验误差为10%; 通过OPENSEES有限元软件构建的数值模型能够从宏观反映框架的耗能能力, 模拟峰值荷载为186kN, 与试验误差为12%; 轴压比和长细比都是预应力型钢混凝土构件的敏感性参数, 试件的承载能力随着设计轴压比的增大而增大, 随着长细比的增大而降低, 但过小的长细比导致试件破坏较快, 不利于试件的延性; 预应力作用对滞回曲线的延性影响并不明显; 根据截面力学性能、构件几何参数, 通过线性回归手段构建的恢复力模型可以良好拟合该类型框架的滞回特性。
关键词: 预应力, 型钢混凝土, 组合框架, 有限元分析, 恢复力模型
引用格式: 姜小琴, 刘嘉琪, 王琨. 预应力型钢混凝土框架恢复力特性研究[J]. 工程材料与结构, 2024, 3(1): 14-24.
文章类型: 研究性论文
收稿日期: 2023-12-07
接收日期: 2024-01-08
出版日期: 2024-03-28
0 引言
预应力型钢混凝土构件相比于普通钢筋混凝土构件具备抗震性能高、荷载承受能力强的优势，在实际施工中获得了广泛的使用，特别是超大跨度和套建增层框架构件中[1-4]。恢复力模型作为描述结构或构件在荷载作用下结构力与结构变形关系的一种数学模型，能较全面的体现其抗震性能，被国内外学者广泛研究。
目前，薛伟辰等[5]建立了预应力钢骨混凝土梁关于弯矩与转角参数的恢复力模型;葛继平[6]通过回归分析的手段构建了由方钢管混凝土柱与钢梁组成的半刚性节点的弯矩-转角恢复力模型;张继承[7]建立了T型钢管混凝土框架的恢复力模型;胡立黎[8]分析得出了钢筋混凝土深梁填充钢框架的三折线恢复力模型。可以看出，国内外学者对于恢复力模型的研究较为充分，主要涵盖了梁、柱、框架。但对于本文提出的新型型钢混凝土框架结构恢复力模型的研究还较为匮乏。
因此，本文将建立单榀预应力型钢混凝土框架有限元模型，与先前所做实验加以对比。利用ABAQUS软件中三维实体单元所构建的模型，探讨了其破坏形态与应力分布。通过用OpenSEES软件中纤维梁、柱单元所构建的模型进行参数分析，以探讨预应力型钢混凝土框架的抗震特性，并利用理论分析出此类单榀组合框架的荷载-位移恢复力模型，并与数据计算结果比较，为结构弹塑性动力分析的简化提供了帮助。
1 试验概况
文献[9,10]进行了框架抗震性能试验。试件尺寸及配筋如图1所示。框架梁内置焊接H型钢尺寸为HN130mm×50mm×4mm×8mm，预应力钢筋直径为12.7mm，居中布置。为方便预应力筋的居中布置，焊接H型钢腹板偏置于一侧。柱内配置焊接H型钢的尺寸为HN130mm×110mm×4mm×10mm。梁柱内纵筋均采用HRB400钢筋，焊接H型钢所采用的钢板强度等级均为Q235级，箍筋强度等级均为HPB235。试件采用现场浇注，实测混凝土立方体抗压强度为fcu=41.0MPa，棱柱体抗压强度为fc=27.21MPa，实测直径为14mm、12mm和6mm的钢筋的屈服强度fy分别为398MPa、487MPa和305MPa，实测厚度为4mm、8mm、10mm的钢板的屈服强度fa分别为360MPa、295MPa和336MPa。
试验加载方案如图2所示。两个竖向集中荷载均作用于框架梁上，大小为40kN，并在加载过程中保持恒定。之后，水平低周往复荷载沿框架梁轴线施加。加载制度为力位移混合控制加载，如图3所示。
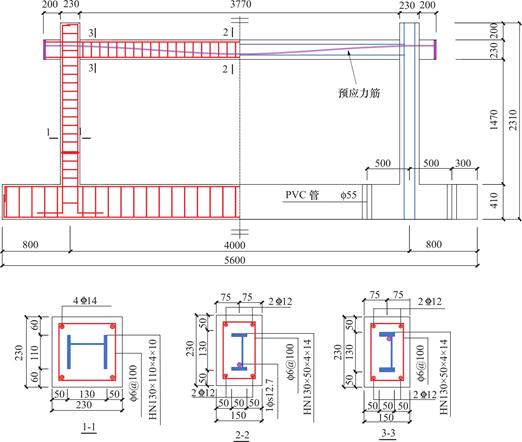
图1 预应力型钢混凝土框架具体参数示意图(mm)
Fig.1 Schematic diagram of the specific parameters of the prestressed steel and concrete frame(mm)
图2 加载受力简图
Fig.2 Schematic diagram of loading scheme
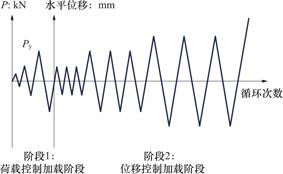
图3 加载制度示意图
Fig.3 Schematic diagram of loading regime
2 有限元模拟
为充分研究该类型框架在水平荷载下的抗震性能，本文通过ABAQUS 软件建立数值模型，并开展细致的力学性能分析。
2.1 有限元模型的建立
2.1.1 材料本构关系
本文将预应力型钢混凝土框架梁柱截面的混凝土分为箍筋约束区和保护层两个部分，如图4所示。
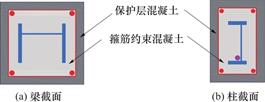
图4 梁柱截面划分
Fig.4 Section division of beam and column
在模拟中，对于约束混凝土的本构关系，采用韩林海
提出的模型，按式(1)~式(6)计算。
σc=
(1)
k=
(2)
Edes=
(3)
σc0=f'c(4)
εc0=0.00245+0.0122f
(5)
ε0.85=0.225ρv
+εc0(6)
式中，f'c 为混凝土圆柱体抗压强度，
为峰值压应变，ρh为体积配箍率，fyh为箍筋屈服强度，s为箍筋间距，Bc为箍筋所圈范围内部混凝土的宽度。
对于其余混凝土部分，其本构关系采用GB 50010—2010中双参数本构模型[12]，按式(7)、(8)计算。
σc=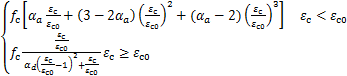
(7)
σt=
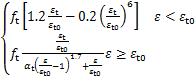(8)
式中，fc为混凝土抗压强度，αa、αd为受压本构曲线上升段、下降段参数，ft0为混凝土抗拉强度，εt0为ft相应的混凝土峰值拉应变，αt为单轴受拉下降段参数。
在混凝土应力达到抗压或抗拉强度之前，不考虑其损伤。在达到抗压或抗拉强度之后的下降段，混凝土损伤指标d按公式(9)计算[13]。
d=1-
(9)
式中，f为抗压或抗拉强度，σ为混凝土受压或受拉应力。
梁柱内H形钢、纵筋和箍筋的单轴应力-应变关系均按式(10)计算。预应力筋部分采用郑文忠[14]提出的本构关系模型，按式(11)计算。
σs=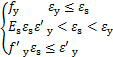
(10)
σp=
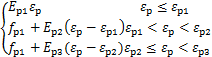(11)
式中，fy、f'y分别为抗拉和抗压屈服强度，Es为钢材的弹性模量，εy、ε'y分别为抗拉和抗压屈服应变;Ep1、Ep2分别为弹性和非弹性阶段的刚度，Ep3为屈服刚度，fp1、εp1，fp2、εp2，fp3、εp3分别为预应力筋比例极限点、屈服点、破坏极限点的应力应变。
2.1.2 单元类型与接触
根据文献[9，10]的试件实际尺寸，本文建立了的数值模型如图5所示。有限元模型主要包含型钢骨架、钢筋骨架、预应力筋及混凝土框架4个部件。
由于试验结果未发现梁端和柱底塑性铰区发生粘结滑移破坏，表明型钢和钢筋骨架与混凝土粘结可靠。因此，在有限元模型建立中，采用内置区域约束模拟型钢骨架、钢筋骨架、预应力筋与混凝土的相互作用。为避免局压破坏，在混凝土梁上设置了两个钢性垫板，采用绑定约束。
2.1.3 荷载及边界条件
为避免局压破坏，梁上竖向集中荷载施加在钢性垫板上，水平荷载沿梁框架柱的轴线方向施加，采用位移控制。框架柱底面施加固接约束。ABAQUS计算模型的边界条件如图5所示。
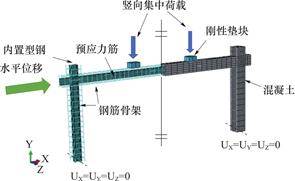
图5 有限元模型受力情况
Fig.5 The force of the finite element model
2.2 数值计算结果
经过大量试算，有限元模型在低周往复荷载下无法收敛，而滞回计算结果和试验差别很大，在此仅给出单向加载的模拟结果。
2.2.1 有限元模拟与试验结果对比
图6为预应力型钢混凝土框架ABAQUS有限元模拟与试验结果对比，可见，模拟所得的骨架曲线峰值荷载(191kN)略小于试验所得的峰值荷载(207kN)，误差为10%。
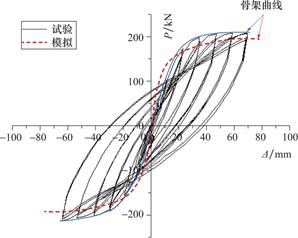
图6 模拟与试验骨架曲线比较
Fig.6 Comparison of calculation and test skeleton curve
2.2.2 破坏形态
图6给出了预应力型钢混凝土框架破坏时混凝土应变及型钢和钢筋的应力分布。从图7(a)和7(b)可以看出，在水平向右单调加载作用下，框架梁左端上部和右端下部的混凝土应变均超过0.0033，即混凝土被压碎。从图7(c)和图7(d)可以看出，梁两端和柱底部的受拉型钢翼缘和纵筋均超过了相应的屈服强度，表明框架梁两端和柱底均出现了塑性铰。前述破坏现象与试验一致。此外，通过有限元分析还可以发现，预应力筋在梁右上端部也达到了屈服强度。
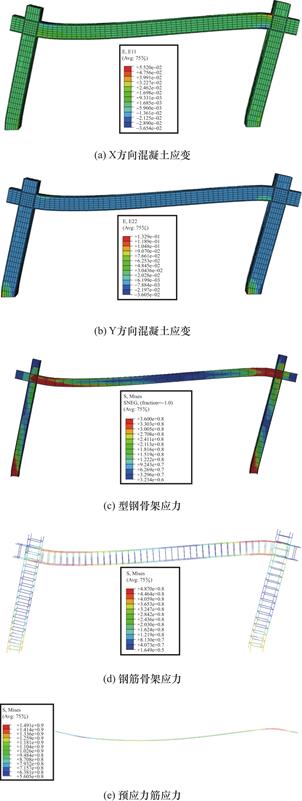
图7 PSRCF应变及应力分布
Fig.7 Strain and stress distribution of PSRCF
3 基于纤维梁柱单元的滞回性能分析
由于使用ABAQUS进行滞回模拟时，计算收敛困难、滞回曲线不理想，另外，考虑分析参数时会造成模型修改幅度很大，所以，本节将通过OpenSEES抗震分析平台对预应力型钢混凝土框架进行低周往复荷载模拟分析。
3.1 预应力作用
本文将预应力分成二个阶段施加，并运用等效原理[15]建立了预应力框架的有限元数值模型。如图8所示。
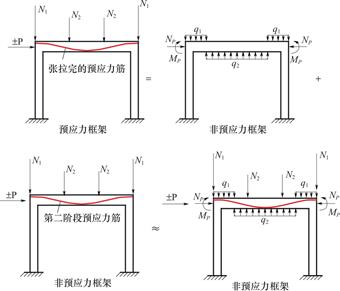
图8 预应力作用简化示意图
Fig.8 Simplified diagram of prestressing effect
3.2 材料本构关系
3.2.1 混凝土
梁柱混凝土采用OpenSEES提供的Concrete01模型，该模型不考虑混凝土受拉的影响，其单轴受压应力-应变(σc-
)关系为Scott修正的Kent-Park模型[16-17]，详见公式(12)。式中，fc为混凝土圆柱体抗压强度，K是约束的影响考虑强度增加的系数，ε0为峰值应变，εu为极限压应变。此外，该模型的滞回规则采用了Karsan-Jirsa提供的滞回关系[17]。
σc=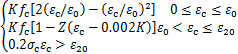
(12)
3.2.2 型钢和钢筋
型钢翼缘和腹板以及纵向钢筋的本构关系采用OpenSEES提供的steel02模型，该模型即双线性随动强化模型。
3.2.3 预应力筋
预应力两阶段原理指出，预应力筋第一阶段(从张拉到有效预应力的建立)是用于产生等效荷载的;第二阶段(在等效预应力建立以后)中预应力筋高于有效预应力的富余强度像普通钢筋一样用于提供抗力。因此，第二阶段预应力筋可采用OpenSEES提供的Elastic Perfectly Plastic Material模型，其应力-应变(σp-εp)关系见式(13)。式中fp0.2为条件屈服强度，σpe为预应力筋的有效预应力，Ep为初始刚度，εp0为第二阶段预应力筋条件屈服应变，按εp0=(fp0.2-σpe)/Ep计算。
σp=
(13)
3.3 模型的建立
依据3.1节的简化方法，本文基于Open SEES抗震分析平台建立了采用纤维梁柱单元的单榀预应力型钢混凝土框架的数值分析模型，如图9(a)所示。该模型中，框架梁采用集中塑性铰模型，按照预应力等效荷载分布、竖向荷载位置和跨中划分为六个单元，单元节点分别设置在梁端、跨中、预应力筋反弯点和竖向集中荷载作用点。框架柱采用集中塑性铰模型，每根柱划分为1个单元。框架柱底与基础刚性连接，柱顶竖向集中力N1作用在节点3和4上，梁上集中荷载N2施加在节点5和6上，水平往复荷载P作用在框架梁左端的节点3处。
为简化分析仅将梁、柱截面划分未箍筋约束的混凝土核心区和保护层，如图9(b)所示，并分别采用约束和非约束混凝土模型。
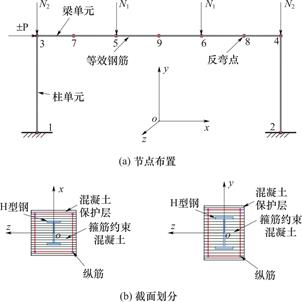
图9 PSRCF杆系有限元模型
Fig.9 Finite element model of PSRCF
3.4 计算结果对比
数值计算和实验滞回曲线如图10所示。模拟结果和试验结果在峰值荷载、极限位移和滞回曲线形状等方面总体吻合。
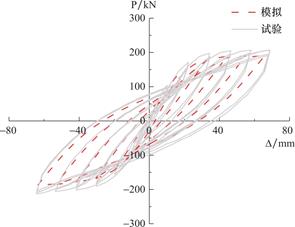
图10 有限元模拟结果
Fig.10 Results of finite element simulation
4 滞回性能参数分析
为进一步探讨预应力型钢混凝土框架的受力性能，本文对柱长细比β、轴压比n0、混凝土强度fc、预应力度λ等参数开展了参数分析。
4.1 长细比
由图11(a)至图11(d)可见，由于柱长细比的增加，峰值荷载呈现下降的态势，具体而言，长细比为12的试件峰值荷载为144.51kN，而长细比为6的试件峰值荷载为311.97kN，但是较小的长细比破坏较快，长细比较大的试件延性较好。根据图11(f)中的结果，在相同位移条件下，滞回环面积随着长细比增加而减少。此外，通过观察图11(g)，我们能够知道割线刚度K和长细比之间存在联系，具体来说，在相同位置下，割线刚度随着柱长细比的增加而减少，刚度退化效应也显得更为突出。另外，柱长细较小的框架在较小位移时显示出更明显的刚度退化效应，但由于位移的增加，不同长细比的框架刚度退化也逐步趋于一致。综上所述，我们可得出如下结论:框架的滞回特性受柱长细比的影响，柱长细比的提高会减少框架的峰值荷载，从而增加相应的位移。与此同时，框架的长细比增大会减少了其耗能能力和割线刚度，尤其在较小位移时刚度退化效果表现得更为明显。但是，在较大的位移下，不同长细比的框架的刚度退化趋势也逐步趋于一致。
4.2 设计轴压比
通过图12(a)，可看出由于轴压比的提高，骨架曲线的峰值荷载先增加后降低。另外，超出0.5的轴压比使得框架的极限位移明显减少，框架的延性也明显降低。根据图12(b)，在加载位移较小的情况下，不同轴压比下的框架的滞回曲线体积比较接近。图12(c)中显示了割线刚度K和轴压比之间的联系关系。割线刚度随着移动的增加而减少。
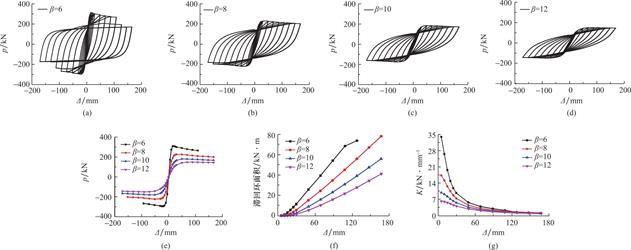
图11 长细比对滞回曲线性能的影响
Fig.11 Effect of length to slenderness ratio on hysteresis curve performance
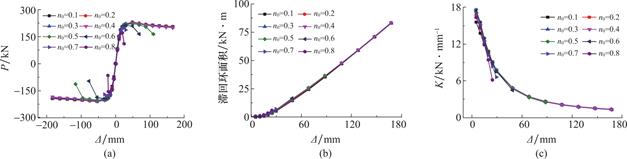
图12 轴压比对滞回曲线性能的影响
Fig.12 Effect of axial compressive ratio on hysteresis performance
4.3 立方体混凝土强度
通过图13的结果，可得出:首先，在立方体混凝土强度增加的前提下，骨架曲线的初始刚度也相应增加，并且峰值荷载也呈现明显增加的态势，混凝土强度为50MPa时，峰值荷载为279kN，而混凝土强度为30MPa时，峰值荷载为245kN，提高混凝土等级能够提高承载能力约为13.5%。其次，在到达峰值荷载后的下降段，各试件的骨架曲线下降幅度相对接近。另外，在同样的位移处，强度更高的混凝土试件所对应的滞回环体积很大，这也说明了其拥有良好的耗能能力。此外，当移动较小时，硬度更高的混凝土试件所对应的割线刚度也较大。
4.4 预应力度
预应力度λ是消压弯矩M0与按短期效应组合计算的弯矩Ms的比值[18]，即λ=M0/M。由于梁内有型钢的存在，预应力作用对框架滞回曲线的影响不显著。由图14可以看出，预应力度对结构的延性几乎没有影响。
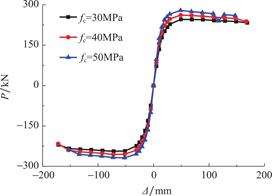
图13 混凝土强度对骨架曲线的影响
Fig.13 Influence of concrete strength on skeleton curves
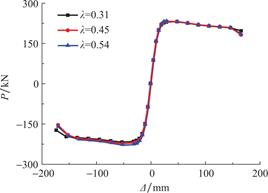
图14 预应力度对骨架曲线的影响
Fig.14 Influence of prestress level on skeleton curves
5 水平荷载-位移恢复力模型
本文基于大量参数分析，回归出了单榀预应力型钢混凝土框架的水平荷载-位移(P-Δ)恢复力模型，该模型适用于单榀预应力型钢混凝土框架结构。
5.1 恢复力模型的建立
图15为所建立的恢复力模型，图中Y和M表示屈服点和峰值点，数字表示恢复力模型在正、反向加卸载过程中的发展顺序[19]。
恢复力模型需确定屈服刚度Ky、水平屈服荷载Py、水平峰值荷载Pm、峰值点位移Δm、下降段刚度Kd等参数。通过前述分析可知，预应力度对骨架曲线影响不大，因此为简化分析，本文将轴压比n0和长细比β作为建立恢复力模型的主要因素。
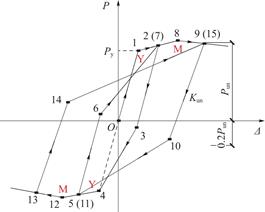
图15 P-Δ恢复力模型示意图
Fig.15 Schematic diagram of the resilience model
根据梁柱截面力学性能等参数，通过线性回归建立框架初始刚度Ky的表达式，见式(14)。其中，Ke为框架的侧向刚度，可按式(15)、(16)计算。
Ky=(1.412+0.396n0-0.043β-
0.691
+0.066n0β)Ke (14)
Ke=
·
(15)
k=
(16)
式中，EIc为柱截面刚度，EIb为梁截面刚度，L1为梁长度，L2为柱高度。
经回归，水平屈服荷载Py可按式(17)计算。其中，Mbu1、Mbu2、Mcu1和Mcu2分别为梁柱截的抗弯承载力。
Py=(1.35-1.17n0-0.0181β+
1.66+0.044n0β)·
(17)
经分析峰值荷载Pm、峰值荷载Pm对应的位移Δm、下降段刚度Kd的表达式为可按式(18)、(19)计算。
Pm=(1.39-1.02n0-0.0071β+
1.62+0.033n0β)·
(18)
Δm=(-2.692+4.314n0+0.997β-4.788-
0.171n0β+0.05β2)
(19)
Kd=
Ke(20)
当水平荷载未达到屈服荷载Py前，卸载刚度采用屈服刚度，即Kun=Ky。当水平荷载超过正向或负向的屈服荷载Py，卸载刚度Kun按式(21)计算。
Kun=0.925
Ky(21)
5.2 恢复力模型验证
图16为恢复力模型验证结果，可见，数值计算滞回曲线与滞回模型较为接近，表明恢复力模型可靠。
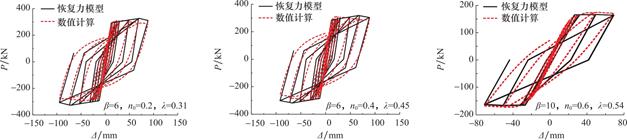
图16 数值计算与恢复力模型对比
Fig.16 Comparison of numerical calculation and restoring force model
6 结论
通过数值模拟的手段对预应力型钢混凝土组合框架进行了抗震性能方面的研究并且推导恢复力模型关系曲线，得到如下结论:
(1)通过ABAQUS建立的数值模型在单调加载下的骨架曲线与试验骨架曲线较为接近，能合理反映试验结果;
(2)通过OpenSEES所建立的有限元模型在低周往复加载作用下荷载位移曲线与试验曲线较为接近。导出滞回环面积饱满;
(3)柱长细比和轴压比对滞回曲线结果有重要影响，柱长细比增加，延性增加;轴压比增加，预应力及非预应力型钢混凝土框架位移延性变小，表明其变形能力降低。
(4)本文通过理论分析所推导的恢复力模型关系与有限元模拟结果较为相近，可为工程实际应用做参考。
利益冲突: 作者声明无利益冲突。
[②] *通讯作者 Corresponding author:刘嘉琪，lpjinqaz@163.com
收稿日期:2023-12-07; 录用日期:2024-01-08; 发表日期:2024-03-28
基金项目:本项研究得到了国家自然科学基金项目预制预应力桁架式钢骨砼框架承载性能研究(资助号51578478)的资助。
参考文献(References)
[1] Xueyu Xiong, Gangfeng Yao, Xiaozu Su, Experimental and numerical studies on seismic behavior of bonded and unbonded prestressed steel reinforced concrete frame beam[J]. Engineering Structures, 2018, 167: 567-581.
https://doi.org/10.1016/j.engstruct.2018.04.024
[2] Xueyu Xiong, Gangfeng Yao, Studies on the static behaviors of unbonded prestressed steel reinforced low strength concrete rectangular frame beams[J]. Engineering Structures, 2018, 171: 982-991.
https://doi.org/10.1016/j.engstruct.2018.02.007
[3] Kun Wang, Shenfeng Yuan, Dafu Cao, Wenzhong Zheng. Experimental and numerical investigation on frame structure composed of steel reinforced concrete beam and angle-steel concrete column under dynamic loading[J]. International Journal of Civil Engineering, 2015, 13(2): 137-147.
https://doi.org/10.22068/ijce.13.2.137
[4] Lou T, Lopes S M R, Lopes A V. Numerical modeling of externally prestressed steel-concrete composite beams[J]. Constr Steel Res, 2016; 121: 229-36.
https://doi.org/10.1016/j.jcsr.2016.02.008
[5] 薛伟辰, 杨枫, 苏旭霖, 等. 预应力钢骨混凝土梁低周反复荷载试验研究[J]. 哈尔滨工业大学学报, 2007, 39(8): 1185-1190.
https://doi.org/10.3321/j.issn:0367-6234.2007.08.002
[6] 葛继平, 宗周红, 杨强跃. 方钢管混凝土柱与钢梁半刚性连接节点的恢复力本构模型[J]. 地震工程与工程振动, 2005(06): 81-87.
https://doi.org/10.13197/j.eeev.2005.06.014
[7] 张继承, 周灵姣, 吕行, 等. T 形钢管混凝土柱-钢梁平面框架抗震性能研究[J]. 建筑结构学报, 2017, 38(03): 76-83.
https://doi.org/10.14006/j.jzjgxb.2017.03.008
[8] 胡立黎, 郑宏, 肖峰. 钢筋混凝土深梁填充钢框架的恢复力模型[J]. 土木工程学报, 2010, 43(9): 49-54.
https://doi.org/10.15951/j.tmgcxb.2010.09.011
[9] 傅传国, 李玉莹 孙晓波, 等. 预应力及非预应力型钢混凝土框架受力及抗震性能试验研究[J]. 建筑结构学报, 2012, 31(8): 15-21.
https://doi.org/10.14006/j.jzjgxb.2010.08.004
[10] 顾钊. 预应力型钢混凝土框架力学性能非线性分析 [D]. 扬州: 扬州大学, 2020.
https://doi.org/10.27441/d.cnki.gyzdu.2019.000900
[11] 韩林海. 钢管混凝土结构-理论与实践(第二版)[M]. 北京: 科学出版社. 2007.
[12] 中华人民共和国建设部. GB50010-2010. 混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2014: 206-208.
[13] T. Yu, J. Teng, Y. Wong, et al. Finite element modeling of confined concrete-II: Plastic-damage model[J]. Engineering Structures, 2010, 32(3): 680-691.
https://doi.org/10.1016/j.engstruct.2009.11.013
[14] 郑文忠, 侯晓萌, 闫凯. 预应力混凝土高温性能及抗火设计[M]. 哈尔滨: 哈尔滨工业大学出版社, 2012.
[15] 郑文忠, 王英. 预应力混凝土房屋结构设计统一方法与实例[M]. 哈尔滨: 黑龙江科学技术出版社, 1998.
[16] Park R, Priestlely M J N, Gill W D. Ductility of squareconfined concrete columns[J]. Journal of the Structural Division, 1982, 108(4): 929-950.
https://doi.org/10.1016/0022-1694(82)90165-2
[17] Scott B D, Park R, Priestley M J N. Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rates[C]//Proceedings of ACI Journal, [S. l. ]: ACI, 1982, 79: 13-27.
https://doi.org/10.1016/0378-7788(82)90060-3
[18] 王琨, 袁沈峰, 曹大富, 等. 型钢混凝土梁-角钢混凝土柱框架恢复力模型特性研究[J]. 北京理工大学学报, 2014, 34(10): 1012-1017+1023.
https://doi.org/10.15918/j.tbit1001-0645.2014.10.005
[19] Kun Wang, Xiao-Feng Lu, Shen-FengYuan, Da-Fu Cao, Zai-Xian Chen. Analysis on hysteretic behavior of composite frames with concrete-encased CFST columns[J]. Journal of Constructional Steel Research, 2017, 135: 176-186.
https://doi.org/10.1016/j.jcsr.2017.03.011
Research on Restoring Force Model Characteristics of Prestressed Steel Reinforced Concrete Frames
(1. Yangzhou Municipal Government, Facility Management Center, Yangzhou 225000, China
2. Yangzhou University, College of Architectural Science and Engineering, Yangzhou 225000, China)
Abstract: On the basis of reasonable selection of material constitutive model, the numerical model of singlebay prestressed section steel-concrete frame. was constructed by using ABAQUS and Open SEES finite element software, respectively, and numerical analyses of the whole process of monotonic and hysteretic force were carried out, and the hysteretic characteristics of this type of frame. structure were analyzed. The main parameters affecting the hysteresis characteristics of this type of frame. were determined through parametric analysis, and the restoring force model was established as a result. The results show that: the numerical model constructed by ABAQUS software can intuitively reflect the damage morphology and stress distribution of the frame, and the simulated peak load is 191kN, with an error of 10% from the test; the numerical model constructed by OPENSEES finite element software can macroscopically reflect the energy-consuming capacity of the frame, and the simulated peak load is 186kN, with an error of 12% from the test; both the axial compression ratio and the length to slenderness ratio are sensitive parameters of prestressed steel and concrete members, the load capacity of the specimen increases with the increase of the design axial compression ratio, and decreases with the increase of the length and slenderness ratio, but too small length and slenderness ratio leads to the destruction of the specimen faster, which is not conducive to the ductility of the specimen; the prestressing effect on the ductility of the hysteresis curve is not obvious; according to the mechanical properties of the section, the geometrical parameters of the member, the restoring force constructed by means of linear regression can be a good fit for this type of frame.
Keywords: Prestress, steel reinforce concrete, composite frame, finite element analysis, restoring force model
Citation: JIANG Xiaoqin, LIU Jiaqi, WANG Kun. Research on restoring force model characteristics of prestressed steel reinforced concrete frames[J]. Engineering Materials and Structures 2024, 3(1): 14-24.