

基于离散元法的砂粒分拣直线振动筛筛分性能仿真
(华北水利水电大学, 郑州 450046)
摘要: 为了响应黄河流域生态保护和高质量发展的战略部署, 解决黄河下游河砂混合物的分离问题, 提高利用直线振动筛进行河砂分离的筛分效率, 查阅大量文献表明, 在直线振动筛的筛分过程中, 影响筛分效率及筛分质量的主要因素有: 振动频率、振幅和筛面倾角。因此, 本文以砂粒作为研究对象, 基于离散单元法 (EDEM) 对砂粒在直线振动筛不同参数下的筛分过程进行模拟, 使用Hertz-Mindlin with JKR接触模型, 通过改变振动频率、振幅、筛面倾角的参数, 观察其对筛分性能的影响及物料筛分过程的变化, 以砂粒的筛分效率作为衡量标准, 获得了最优筛分性能的振动参数组。通过分析仿真模拟结果发现, 直线振动筛的最优振动参数组为: 振动频率f=25Hz、振幅A=4mm、筛面倾角φ=4°, 此时筛分效率可以达到95. 77%。本研究结果表明利用离散元法对于不同工艺参数产生的筛分效率具有很好的可靠性, 该研究可为振动筛的参数选择提供相应的参考。
DOI: 10.48014/fcmet.20231230001
引用格式: 高丹, 吴林峰, 胡凯钦, 等. 基于离散元法的砂粒分拣直线振动筛筛分性能仿真[J]. 中国机械工程技术学报, 2024, 3(2): 32-40.
文章类型: 研究性论文
收稿日期: 2023-12-30
接收日期: 2024-01-14
出版日期: 2024-06-28
0 前言
由于黄河含砂量极大,会造成河床淤积和河道变浅、泥沙淤塞水库和堤坝、土地退化和农作物受灾等危害[1],黄河也成为了世界上最复杂难治的河流,黄河下游是我国重要的工农业生产基地,是黄河防洪的重中之重,关系到经济安全、生态安全和国家安全[2]。为了响应黄河流域生态保护和高质量发展的战略部署[3],依据《水法》、《河道管理条例》,在确保防洪及生态安全的前提下,科学、有序地开采并利用黄河河道的砂[4],促进沿黄经济发展。
目前黄河流域主要采用挖砂船进行采集河砂[5,6],经过前期的勘测,在确定采砂的位置后,利用挖掘机、吸砂管、输送带等装置,将采集的泥沙输送到岸上,但是采集上来的泥沙混合物数量很多,需要占用较大的场地或者容器存放,直接外运没有合适的使用场合[7],就地自然放置会在成空气污染及土地污染[8]。为了避免二次污染,将采集上岸的河沙清洗后再次进行烘干,如何对烘干后的河砂进行过滤处理并有效利用,是当下需要解决的一个技术问题。
烘干后为了提取合适的河砂,需要借助于筛分装置,像固定筛、圆筒筛、直线振动筛等,固定筛通常固定安装在地面上,适用于筛分较大的物料,例如大块的煤、焦炭、石子等[9];圆筒筛由一个圆筒形的筛网、支撑架和驱动装置组成,物料从圆筒的上面进入后经过筛网,粗物料从圆筒的另一侧排出,但转速很低,工作面积小、筛分效率低[10];考虑到黄河流域下游的河砂粒径多为中砂和细砂[11],本文借鉴直线振动筛的工作原理,利用激振系统产生的激振力带动筛箱进行运动,通过筛面上的筛孔将分散砂粒的混合物按粒度大小进行筛分,过滤掉混合物中的杂质。直线振动筛具有易于实现不同的振动方式、筛分效率高等优势。
筛分后的河砂不仅用于建筑、修路材料、人造大理石、养殖美化外,还可用于农田种植和土地改良等农业生产及种植领域[12-13],因此,在筛分过程中提高砂粒的筛分效率受到国内科研机构及相关部门的重视[14]。
为了提高河砂的筛分效率,利用离散元法(discrete element method,DEM)模拟直线振动筛的筛分过程,优化振动筛的参数选择,该方法在采矿工程、物料分选、岩土工程等领域得到了广泛应用,在多学科交叉的研究领域逐步受到广泛关注。王桂峰等[15]基于离散元法进行仿真模拟,并在此过程中分析砂粒的筛分流程,研究了当筛分参数不同时,筛分效率可能受到的影响。王秉等[16]基于离散元法进行仿真模拟,分析了玉米在振动筛上的运动情况,根据筛分情况优化了振动筛的结构。周剑萍等[17]基于离散元法进行仿真模拟,模拟了湿颗粒的筛分过程,在仿真结果中得到了筛分的首选构参数。
本研究基于离散元法进行仿真模拟,可直观看到在直线振动筛不同参数的情况下,砂粒的运动和透筛过程,分析对筛分性能产生影响的各个因素,而筛分性能主要涵盖颗粒的透筛数量、筛分效率两部分,为以后直线振动筛上颗粒群的工作参数及直线振动筛的结构设计提供参考。
1 直线振动筛的总体设计与工作原理
1.1 总体设计
利用直线振动筛的工作原理,使激振系统产生的激振力带动直线振动筛的筛箱运动,河砂经过筛网实现过滤和分拣。图1所示为振动筛的三维模型。该筛分装置的组成主要包括以下几个方面:筛箱、筛框、橡胶弹簧、激振系统、筛网、进出料装置、支架等。该直线振动筛利用向下倾斜的筛面,加上两台激振器产生的激振力有效缓解了物料在筛面上的堆积情况,拥有良好的筛分性能[18],振动筛工作时,2台振动电机做相对运转时,偏心块会产生两个方向的激振力,横向激振力由于电机的相对运转而因此相互抵消,纵向激振力由于电机的同向运转而因此相互叠加,最终使物料在筛网上进行往复直线振动。
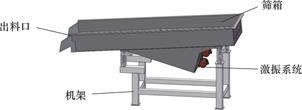
图1 直线振动筛模型
Fig.1 Linear vibrating screen model
1.2 模型简化与参数分析
图2为该装置的运动简化模型,O点为装置筛箱的质心,过O点建立坐标系XOZ,X轴沿水平方向,Z轴沿竖直方向,装置上振动电机的激振力方向与筛箱振动方向均过筛箱的质心O;筛框与X轴的夹角为筛面的倾角α,筛箱的振动方向与筛面的夹角为振动筛的方向角β。
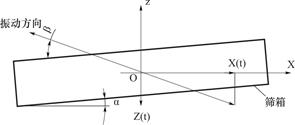
图2 振动筛运动简化模型
Fig.2 Simplified model of vibrating screen motion
一般来说,直线振动筛筛箱上的各点的运动均是沿振动方向做简谐运动,所以位移可表示为:
S=Asinωt,ωt=φ(1)
式中,![]() 表示位移,
表示位移,![]() 为振幅,
为振幅,![]() 为振动频率,
为振动频率,![]() 为时间,
为时间,![]() 为振动相角。
为振动相角。
1.3 工作原理
该直线振动筛的工作原理图如图3所示,规格相同的两个激振器共同组成了该筛分装置的激振系统,两轴上激振器偏心块的偏心质量以等速反向回转[19],在安装时,激振器两轴的位置与y-y轴线是呈对称分布的,且y-y轴线不仅过直线振动筛筛箱的质心也与x轴的水平方向形成一个45°夹角。机器在回转运动过程中,将此时偏心轮所产生的离心力进行分解,分别分解到x轴、y轴方向,由于偏心轮的转动是同步但反向的运动,因此两个激振器在沿x-x和y-y方向上的离心力也不同,沿x-x方向相互抵消,沿y-y方向相互叠加[20],由此,振动筛在运动过程中所受到的激振力是沿y-y方向,最终这也是驱动直线振动筛做往复直线运动的动力源泉。在图4中,当偏心轮转到图4的(a)和(c)位置时,产生的离心力叠加为合力,这时激振力达到顶峰状态,当偏心轮转到图4的(b)和(d)位置时,产生的离心力相互抵消,这时激振力为零。
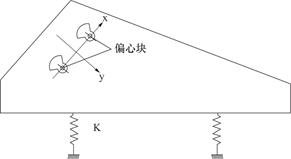
图3 直线振动筛工作原理图
Fig.3 Working principle diagram of linear vibrating screen working principle diagram
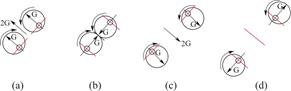
图4 激振器工作原理图
Fig.4 Shaker working principle diagram
2 振动筛筛分离散元模型及仿真参数
2.1 振动筛筛分离散元模型
EDEM可用于仿真模拟和分析农业、工业及采矿业等领域颗粒处理及其制造设备的生成过程,其主要分为3大模块:Creator、Simulator、Analyst[21]。如图5所示,在Creator模块中,以球形颗粒代替砂粒建立颗粒的模型,平均粒径为0.5mm和1.0mm,标准差为0.5mm。选用Hertz-Mindlin with JKR接触模型,颗粒产生的速度是0.1kg/s,其他试验条件如表1和表2所示。在Simulator模块中,定义仿真的时间为10s,调整瑞丽时间步和网格大小。在Analyst模块中,提取相应的仿真数据,像颗粒的透筛数量,赋予不同的颜色时可看出颗粒粒径的大小。
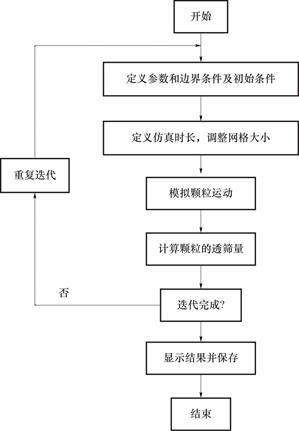
图5 EDEM计算流程
Fig.5 EDEM calculation fiow
本文主要针对3个振动参数(振动频率、振幅、筛面倾角)使用离散元软件EDEM进行模拟筛分的过程,观察各参数的变化对筛分效率的影响[22]。选用的各参数数据为:振动频率25、30、40、50、60Hz,振幅2、4、5、6、7mm,筛面倾角2°、3°、4°、5°、6°。
表1 材料属性参数
Table 1 Material property parameters
|
材料 |
泊松比 |
密度/(kg/m3) |
剪切模量(/Pa) |
|
砂 |
0.25 |
2650 |
2.2×10e^8 |
|
杂质(石块) |
0.2 |
2500 |
3.5×10e^8 |
|
筛箱(不锈钢) |
0.3 |
7850 |
8.0×10e^10 |
表2 材料间的碰撞系数
Table 2 Collision coefficients between materials
|
接触系数 |
恢复系数 |
静摩擦系数 |
滚动摩擦系数 |
|
砂-砂 |
0.40 |
0.5 |
0.05 |
|
砂-杂质 |
0.35 |
2500 |
0.015 |
|
砂-筛箱 |
0.30 |
0.3 |
0.01 |
|
杂质-筛箱 |
0.35 |
0.2 |
0.01 |
|
杂质-杂质 |
0.35 |
0.2 |
0.02 |
2.2 离散元数值模拟筛分过程
振动筛从0s开始运动,然后采用“落雨法”产生多种粒径不同的颗粒,直线振动筛开始以频率15Hz、振幅为5mm、筛面倾角为5°的参数进行直线振动。颗粒群在筛面上的运动和筛分主要分为四个过程,即静止、松散、分层和透筛。开始时,颗粒从进料口排出,振动筛将颗粒抛出筛面,使其回落并沿筛网向下运动,在振动的过程中,激振器的振动会导致进料颗粒分层,从而使细小的颗粒穿过物料层沉降到筛网表面,而大的颗粒则会上升到顶部,分层后的细颗粒有机会通过筛面网口,成为尺寸不足的物料流,大的颗粒和未透筛的部分颗粒会被送到筛网末端,成为过大颗粒流。随着颗粒越来越多最终将会覆盖整个筛面,当筛上颗粒与筛下颗粒的颗粒质量达到相对稳定时,筛分过程也达到动态稳定的状态。
如图6所示为砂粒的筛分过程,根据砂粒直径的不同将其设置为不同的颜色,颜色越深代表砂粒粒径越大,反之,越浅代表砂粒粒径越小。在开始筛分时,大小不一的砂粒犹如“下雨”般依次落在筛面上,这时,与筛面相接触的部分颗粒与筛孔进行比较,小于筛孔的砂粒会穿透筛面,而没有穿透筛面的颗粒将随着筛面的振动方向向筛面中部运动。如图6(a)、(b)所示。随着入料颗粒的增多和振动筛的运动,筛下的颗粒不断增多,未透筛的颗粒则跟随筛面的振动不断朝着出料端运动,如图6(c)所示。随着筛分的进行,不能透筛的颗粒汇聚在一起形成料流,而且由于筛面的振动,料层比较松散,粒径不同的颗粒出现了分层,部分小颗粒碰到筛面后透过筛孔,未透筛的杂质则向出料端运行,此时振动筛的筛分效果逐渐趋于稳定,如图6(d)所示。
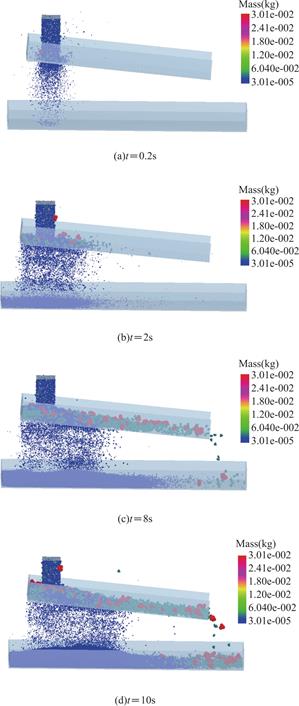
图6 振动筛筛分过程
Fig.6 Vibrating screen screening process
3 工艺参数对筛分效果影响
3.1 直线振动筛筛分物料性能指标
在筛分时,由于振动筛受运动参数、筛孔的形状与筛面开孔率、入料方式、颗粒的粘度等因素的影响,因此,物料在筛分时并不是按照理想状态进行的,实际筛分时,并不是只要颗粒小于筛网尺寸就能通过筛网的,还有一部分小颗粒不能通过筛网而成为了筛上物。为了评价筛分过程中的实际效果,引入筛分效率的概念,对筛分结果进行直观、客观的评价[11]。筛分过程主要分为四个步骤:入料、透筛、输送、排料,因此筛分是连续进行的动态过程,而在这个过程中,筛分效率也会随着时间的改变而变化,而传统的筛分效率计算方法已无法来衡量动态的筛分过程,为此,本文采用公式(2)作为动态筛分效果的衡量指标。
![]() (2)
(2)
式中,![]() 为t时刻的动态筛分效率;
为t时刻的动态筛分效率;![]() 为t时刻所产生的筛下产物重量;
为t时刻所产生的筛下产物重量;![]() 为t时刻物料中所含细颗粒的总重量。
为t时刻物料中所含细颗粒的总重量。
3.2 振动频率对筛分效果的影响
振动频率是使筛网产生往复周期运动的动力源,影响颗粒在筛网上的运动能量,使得周期内的颗粒群重新碰撞、散开,较大的振幅可以让颗粒的弹跳更加剧烈,物料在筛网上的位置和运动方式也得到了重新分配,因此,振幅对筛分效果的影响非常直观,是影响振动筛结构强度的重要参数。根据筛分材料和常用的振幅范围,在仿真时,控制频率、筛面角度及筛孔形状不变,选取了5组数据进行模拟。
在进行仿真试验时,控制振幅及筛面角度不变,振动频率取25Hz、30Hz、40Hz、50Hz、60Hz,其余参数均为基准参数保持不变,计算出颗粒透筛数量、筛分效率并绘制曲线图,如图7所示,可以看出,通过筛网的颗粒数随时间的变化呈递增趋势,从实际生产要求出发,透筛量越大砂粒的生产效率越高。可以看出,当振动频率f=25Hz时,振动筛透筛的数量最多,此时的筛分效果最好。
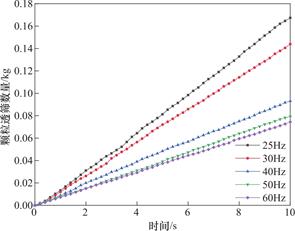
图7 不同频率下的颗粒透筛数
Fig.7 Number of particles passing through the sieve at different frequencies
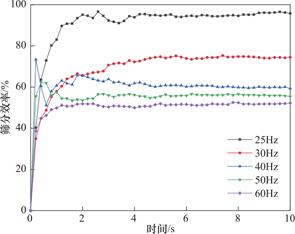
图8 不同频率下的动态筛分效率曲线
Fig.8 Dynamic screening efficiency curves at different frequencies
根据通过筛网的颗粒数和总颗粒数可以得出筛分效率,如图8所示,在振动电机刚启动时,由于电源电压和电流的不足,运行尚不稳定,所以颗粒在开机的前2s出现来回反弹的情况,2s后机器达到稳定状态,动态筛分效率曲线的趋势稳定,而随着频率的增加,曲线的斜率逐渐变小,且每个频率对应的筛分效率相差较大,当频率为25Hz时,振动筛的筛分效率最大,性能最好。
3.3 振动振幅对筛分效果的影响
振幅是指筛子沿着振动方向的位移,影响物料颗粒在筛面上的运动速度,因此,在运行时因该选择合适数值的振幅,振幅过大时,颗粒在筛面上跳动的也就会越剧烈,颗粒输送量大时反而越容易分层,振幅过小时,颗粒在筛面上不发生碰撞,不利于颗粒分层。
在进行仿真试验时,控制频率及筛面角度不变,振幅取2mm、4mm、5mm、6mm、7mm,其余参数均为基准参数保持不变,利用EDEM的传感器模块检测此时筛上、筛下颗粒的数量及大小,可得出颗粒得透筛数量,在经过后期的分析计算也可得出颗粒的筛分效率,根据这些数据并绘制曲线图,如图9所示。由图9可以看出,通过筛网的颗粒呈现先增加后减小的趋势,在振幅A=4mm、5mm时,砂粒的透筛数量居多。
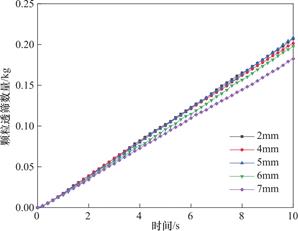
图9 不同振幅下的颗粒透筛数量
Fig.9 Number of particles passing through the sieve at different amplitudes
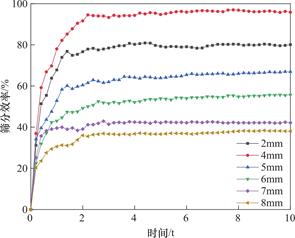
图10 不同振幅下的动态筛分效率曲线
Fig.10 Dynamic screening efficiency curves at different amplitudes
在图10中,当振幅为4mm时筛分效率可达到峰值,而在4mm之后筛分效率随着振幅的增加而减少。这是因为,当振幅较低时,会使颗粒在筛面的X方向的抛掷距离变小,筛面上的颗粒容易形成堆积,此时颗粒与筛面的接触减少,导致筛分效率降低;随着振幅的增大,颗粒在筛面上X方向的抛掷距离变大,使堆积到筛面上的颗粒易于向筛箱的各个方向分散,这时颗粒与筛面的接触增多,加大了透筛率,提高了筛分效率;另外,振幅过大时,颗粒在筛面上的运动较为剧烈,颗粒被抛向空中的次数和时间增加,当这个时间超过筛面的振动周期时,颗粒与筛面接触的次数就会减少,筛分效率则大大降低。
3.4 筛面倾角对筛分效果的影响
筛面倾角主要影响两个方面:颗粒沿筛面方向位移的速度、振动时颗粒被抛射的距离,当筛面倾角越大时,物料在筛面上位移的速度就越大,短时间内就可以筛分完毕,但较大的移动速度会导致颗粒易于滑过筛面,而不能完成筛分,此时的筛分效率降低,反之,当筛面倾角越小时,物料在筛面上位移的速度就越小,即颗粒移动缓慢,而颗粒在筛面上停留的时间越久,就越容易造成物料堆积,不利于自动分级,透气性和筛分性能都降低。
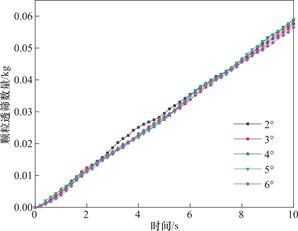
图11 不同倾角下的颗粒透筛数量
Fig.11 Number of particles passing through the sieve at different inclinations
在进行仿真试验时,控制频率及振幅不变,筛面倾角取2°、3°、4°、5°、6°,其余参数均为基准参数保持不变,砂粒随着时间的推移会越来越多,如图11所示,当筛面的倾角越小时,砂粒在筛面上停留的时间也越久,会形成堆积,而适当的增大筛面倾角会有有利于砂粒的透筛。
通过检测砂粒透筛的数量,在经过后期的分析计算可得出砂粒的筛分效率,根据这些数据并绘制曲线图,如图12所示。由图可以得出,筛分效率在筛面倾角为4°和5°前后时筛分效果最好,随着筛分过程的有序进行,颗粒的筛分效率在机器刚启动时迅速增大,2s后步入稳定状态。
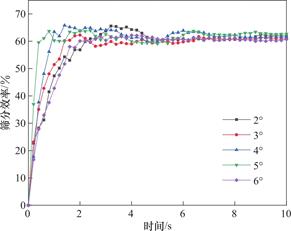
图12 不同倾角下的颗粒透筛数量
Fig.12 Number of particles passing through the sieve at different inclinations
4 结论
本文利用SolidWorks软件绘制了一款直线振动筛分装置,采用离散单元法(EDEM)对振动筛的筛分过程展开仿真分析。主要完成砂粒的分拣工作,为砂粒在不同工程应用提供帮助。通过对仿真结果的分析,绘制出了各工艺参数对筛分效率的影响曲线,得出直线振动筛的最优参数组为:振动频率f=25Hz、振幅A=4mm、筛面倾角φ=4°,此时筛分效率可以达到95.77%,该参数条件下的直线振动筛的筛分效果较好。
利益冲突: 作者声明没有利益冲突。
[①] *通讯作者 Corresponding author:高丹,1821588115@qq.com
收稿日期:2023-12-30; 录用日期:2024-01-14; 发表日期:2024-06-28
参考文献(References)
[1] 申冠卿, 王平, 张原锋. 黄河下游河道泥沙不均衡调整及其对水沙条件的响应[J]. 泥沙研究, 2023, 48(06): 30-37.
https://doi.org/10.16239/j.cnki.0468-155x.2023.06.005.
[2] 冯一凡, 李翅, 李宇, 等. 黄河下游滩区周边城镇空间扩展特征与驱动机制[J]. 地理研究, 2023, 42(04): 955-976.
https://doi.org/10.11821/dlyj020221277
[3] [奋进新征程 建功新时代———伟大变革]推动黄河流域生态保护和高质量发展[J]. 记者观察, 2022(17): 10-12.
https://doi.org/10.3969/j.issn.1004-3799(s).2022.17.003.
[4] 行红磊, 侯晓蕊, 行鑫鑫, 等. 浅谈黄河泥沙的开采和有效利用[J]. 中国水土保持, 2015(06): 39-40.
https://doi.org/10.14123/j.cnki.swcc.2015.0158.
[5] 雷刚. 浅谈绞吸式挖泥船在黄河下游河道疏浚中的应用前景[C]//河海大学, 河北工程大学, 浙江水利水电学院, 北京水利学会, 天津市水利学会. 2023(第二届)城市 水利与洪涝防治学术研讨会论文集. 山东黄河工程集团有限公司; 2023: 6.
https://doi.org/10.26914/c.cnkihy.2023.055602
[6] 喻霁, 朱显玲. 链斗式挖沙船结构强度的分析[J]. 武汉船舶职业技术学院学报, 2017, 16(2): 17-19, 27.
https://doi.org/10.3969/j.issn.1671-8100.2017.02.005.
[7] 曹永潇. 河流健康下的黄河泥沙资源利用[J]. 水利科技与经济, 2015, 21(3): 1-3.
https://doi.org/10.3969/j.issn.1006-7175.2015.03.001.
[8] 王兆印, 王文龙, 田世民. 黄河流域泥沙矿物成分与分布规律[J]. 泥沙研究, 2007(05): 1-8.
https://doi.org/10.16239/j.cnki.0468-155x.2007.05.002.
[9] 姜志勋. 大块处理车间固定筛改造研究[J]. 机械管理开发, 2021, 36(07): 155-156+221.
https://doi.org/10.16525/j.cnki.cn14-1134/th.2021.07.069.
[10] 宗望远, 魏鑫鑫, 马丽娜, 等. 食葵联合收获机圆筒清选 筛结构优化与试验[J]. 农业工程学报, 2023, 39(6): 44-53.
https://doi.org/10.11975/j.issn.1002-6819.202301080.
[11] 王延贵, 胡春宏, 史红玲. 黄河流域泥沙配置状况及其资源化[J]. 中国水土保持科学, 2010, 8(04): 20-26.
https://doi.org/10.16843/j.sswc.2010.04.005.
[12] 于佳月. 土壤因子对怀山药品质影响的研究进展[J]. 农村经济与科技, 2019, 30(9): 8-10.
https://doi.org/10.3969/j.issn.1007-7103.2019.09.004.
[13] 陈怀亮, 任景全, 王连喜, 等. 怀山药的研究现状及其发展的几点建议[J]. 作物杂志, 2012(01): 13-17.
https://doi.org/10.16035/j.issn.1001-7283.2012.01.007.
[14] 施烈焰, 易军, 朱远航, 等. 黄河流域(河南段)土壤环境形势、问题与建议[J]. 河南科技, 2020, 39(31): 147-150.
https://doi.org/10.3969/j.issn.1003-5168.2020.31.049.
[15] 王桂锋, 童昕, 陈艳华, 等. 基于DEM 的振动筛筛分参数对筛分效率影响的研究[J]. 矿山机械, 2010, 38(15): 102-106.
https://doi.org/10.16816/j.cnki.ksjx.2010.15.033
[16] 王秉. 基于DEM 离散元技术的玉米直线振动筛仿真分析[J]. 食品与机械, 2021, 37(10): 89-92.
https://doi.org/10.13652/j.issn.1003-5788.2021.10.016.
[17] 周剑萍, 杜泽鹏. 湿颗粒材料筒仓卸料过程的离散元模拟[J]. 重庆大学学报, 2020, 43(6): 58-64.
https://doi.org/10.11835/j.issn.1000-582X.2020.06.007.
[18] 韩锰, 龚智强, 王成军. 可调平三自由度振动筛结构设计与试验分析[J]. 机械强度, 2022, 44(1): 239-244.
https://doi.org/10.16579/j.issn.1001.9669.2022.01.032.
[19] 刘洁源. 直线振动筛的动力学分析与结构优化设计[D]. 山西: 太原理工大学, 2012.
https://doi.org/10.7666/d.y2156423.
[20] 史朋波. ZKB型直线振动筛的结构动力学分析及优化设计[D]. 邯郸: 河北工程大学, 2018.
https://doi.org/CNKI:CDMD:2.1018.163746
[21] 赵啦啦, 刘初升, 闫俊霞, 等. 振动筛面颗粒流三维离散元法模拟[J]. 中国矿业大学学报, 2010, 39(03): 414-9.
https://doi.org/10.1016/S1876-3804(11)60004-9
[22] 徐天昊. 基于EDEM 的振动筛分参数对效率的对比研究[J]. 南方农机, 2024, 55(1): 166-168.
https://doi.org/10.3969/j.issn.1672-3872.2024.01.045.
Performing A Discrete Element Method Simulation Using A Linear Vibrating Screen for the Sieving Performance Analysis of Sand Particles
(North China University of Water Resources and Electric Power, Zhengzhou 450046, China)
Abstract: In order to respond to the strategic deployment of ecological protection and high-quality development of the Yellow River Basin, to solve the problem of separating river sand mixtures in the lower reaches of the Yellow River, and to improve the screening efficiency of river sand separation by linear vibrating screen, a large amount of literature is consulted, which show that the main factors affecting the screening efficiency and the screening quality during the screening process of linear vibrating screen are: the vibration frequency, the amplitude, and the inclination angle of the screen surface. Therefore, this paper takes sand as the research object, simulates the screening process of sand under different parameters in linear vibrating screen based on the discrete unit method (EDEM) , uses Hertz-Mindlin with JKR contact model, by changing the parameters of vibration frequency, amplitude, screen surface inclination angle, observes its impact on the screening performance and changes in the screening process of the material, and obtains the optimal screening efficiency with the screening efficiency of sand as a measure. As a measure, the vibration parameter set of optimal screening performance was obtained. Through analyzing the simulation results, it is found that the optimal vibration parameters of linear vibrating screen are: vibration frequency f =25Hz, amplitude A =4mm, screen surface inclination angle φ=4°, and the screening efficiency can reach 95. 77%. The results of this study show that the discrete element method has a good reliability for different process parameters to produce screening efficiency, and the study can provide a corresponding reference for the selection of vibrating screen parameters.
Keywords: Linear vibrating screen, discrete element method, screening efficiency, vibration parameters
DOI: 10.48014/fcmet.20231230001
Citation: GAO Dan, WU Linfeng, HU Kaiqin, et al. Performing a discrete element method simulation using a linear vibrating screen for the sieving performance analysis of sand particles[J]. Frontiers of Chinese Mechanical Engineering and Technology, 2024, 3(2): 32-40.