一维双曲守恒律方程基于HWENO限制器的间断型Petrov-Galerkin方法

段晓峰, 高巍^*

(内蒙古大学数学科学学院, 呼和浩特 010021)

摘要: 间断型Petrov-Galerkin方法 (DPG) 是一种区别于DG方法新型双曲守恒律方程数值求解方法, 其具备高精度与模板紧致的特点。然而为了克服高阶线性格式在大梯度解附近的非物理振荡, DPG方法常常需要结合限制器函数来得到高分辨率的数值解图像。本文尝试将HWENO作为限制器函数与DPG进行结合, 求解双曲守恒律方程的间断初值问题。时间离散采用单步高精度SSP Runge-Kutta方法, 采用新的基于HWENO过程作为RKDPG方法的限制器, 仅需一次重构, 就可完成高阶矩的更新, 且无需计算线性权系数。由于精度达不到设计要求, 因此对上述HWENO限制器对上述HWENO限制器中对问题单元的识别方法进行部分改进, 光滑解处使用原有数值解。本文只给出P1元~P3元的计算结果, 该限制器也适用于更高次元的DPG方法。通过数值算例验证了该限制器在问题单元可以有效抑制非物理振荡, 并且保持非问题单元处的原有精度。满足DPG方法的高精度与紧致性特点。具有良好的数值计算效果。

关键词: 间断型Petrov-Galerkin方法, 双曲守恒律, HWENO 限制器, Runge-Kutta

DOI: 10.48014/fcpm.20221019002

引用格式: 段晓峰, 高巍. 一维双曲守恒律方程基于HWENO限制器的间断型Petrov-Galerkin方法[J]. 中国理论数学前沿, 2023, 1(1): 1-13.

文章类型: 研究性论文

收稿日期: 2022-10-21

接收日期: 2022-11-07

出版日期: 2023-06-28

0　引言

双曲守恒律方程是一种重要的数学物理模型。由于其非线性特征，尽管初值函数无间断，随着时间的发展，也会出现间断解。这一特性使得该类方程的数值计算存在着巨大的挑战。过去几十年，研究者们一直在构造求解此类方程的高效数值方法，在FDM，FVM以及FEM的基础上，研究者们提出若干有效的数值计算方法^[1-3]。

在对于Neutron transport 方程进行数值求解时，Reed和Hill^[4]构造了间断型Galerkin方法。其后，B.Cockburn和C-W Shu对DG方法进行了大量扩展与应用^[5-10]。DG方法设定单元之间是不连续的，从而可以在单元内使用分片多项式，在空间与时间上可以设计成高精度阶，灵活性高， 很适合解决复杂边界问题。目前DG方法在很多重要领域得到了快速发展和广泛应用。在求解Compressible N-S方程时，F.Bassi和S.Rebay^[11]首先提出利用间断型Galerkin方法。在此基础上B.Cockburn和C-W Shu^[12]提出局部间断型Galerkin方法，来求解含空间高阶偏导数的方程。与DG方法不同的是，当试验函数空间与检验函数空间不一致时，就产生了间断型Petrov-Galerkin方法(DPG)。 陈大伟等^[13]在RKDG方法和有限体积法的基础上提出间断控制体元方法，它可以看作一种DPG方法。结合local DG和RKCVDFEM方法基础上，文献^[14-16]提出了局部间断型Petrov-Galerkin(LDPG)方法，该方法不仅计算过程简单，而且保持了双曲守恒律方程数值解局部守恒性的优点。J.Qiu和 C-W Shu在2005年提出将WENO作为限制器^[17]与高阶DG方法结合的思路，并获得良好的效果。之后，为克服高阶WENO的大模板与DG紧致模板的冲突，J.Qiu与C-W Shu其后又将HWENO与DG方法进行了有机结合^[18,19]。在WENO与HWENO 过程中，当某一“坏单元”被标记后，基于Gauss积分点的单元多项式要进行重构，且需要计算线性权系数，随着格式精度要求的提高，所需插值模板宽度不断增加。在相同模板宽度下，满足紧致性要求时，会使方法精度更好，边界附近的离散格式更好处理。所以WENO 格式与紧致性要求不符。HWENO在重构时，各阶矩及各积分点所对应的线性权系数不一致，当构造高次元格式时，高阶矩的更新要基于若干次的重构过程，且计算线性权系数过程太复杂。文献^[20]构造一种非线性权系数方法来避免光滑解区域数值解精度的clipping现象。房金伟^[21]在此基础上提出新的HWENO限制器并将其应用到RKDG方法中。该限制器仅需一次重构即可，且不需要计算线性权，大大减少了计算量。

本文对于双曲守恒律方程的空间离散基于间断型Petrov-Galerkin方法，分别使用的一次元、二次元和三次元格式，相应的常微分方程组使用单步高精度SSP Runge-Kutta格式进行时间步求解。并采用上述HWENO限制器，由于精度达不到设计要求，故对上述HWENO限制器进行部分改进^[22]，从而仅需一次重构，就可完成高阶矩的更新。通过光滑因子构造一个简单函数，用来判断方程在某一时刻解的光滑与间断并标记该单元。光滑解处取原有高阶多项式，被标记的间断解处使用重构多项式对各阶矩进行重构。该方法用较少的模板得到重构多项式，使得DPG格式具有很好的紧致性。与原有HWENO限制器相比较，为了重构问题单元的各阶矩该HWENO限制器不再需要进行多次多项式重构以及计算线性权系数，从而减少了计算量。并在文末通过经典算例计算结果验证了该格式的高精度与高分辨率。

1　间断型Petrov-Galerkin方法

1.1　空间离散

一维双曲守恒律方程

(1.1.1)

这里是流通量函数。首先将求解区间剖分成个单元格，，为剖分节点，第j个单元为，单元长度，。

试探函数 基函数选取为Legendre正交基

对应每个基函数的模为

则单元形状函数为

(1.1.2)

其中为单元自由度。

在每个单元上，选取作为插值节点，如图1所示。

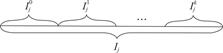
图1　单元I_j控制体积选取

Fig.1　Unit I_j controls volume selection

围绕节点选取控制体积。检验函数基函数选取为

(1.1.3)

将方程(1.1.1)两边同时乘以检验函数，在单元上积分，用代替，用代替。

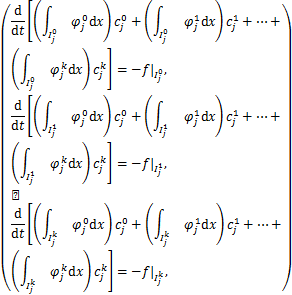
整理得

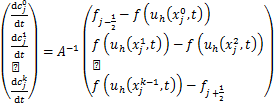(1.1.4)

其中

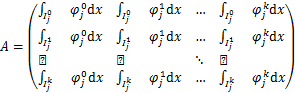(1.1.5)

在单元交界处允许解间断，由于无定义，故用相容单调的Lipschitz数值流通量

(1.1.6)

代替，本文采用Lax-Friedrichs数值流通量，

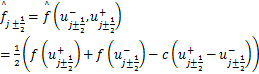(1.1.7)

其中。

至此，DPG格式空间离散完毕，得到如下常微分方程组

(1.1.8)

其中为单元自由度构成的向量。

当基函数取线性元，二次元与三次元时分别对应的矩阵=如下

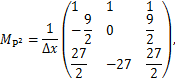
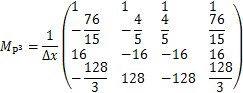
1.2　HWENO限制器

(1)元

为单元的积分平均值，在模板上构造二次多项式满足

(1.2.1)

分别在模板，上构造一次多项式，满足

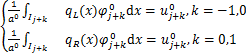(1.2.2)

我们的重构多项式为

(1.2.3)

其中加权系数，满足。

光滑因子取为

(1.2.4)

计算对应的光滑因子

(1.2.5)

取

(1.2.6)

，

其中，

。

取，

当s趋于0时，我们认为这个区间是光滑的，此时取原有数值解。反之s趋于1时，这个区间含有间断，使用重构多项式逼近间断解。

取，。函数图形如图2所示。

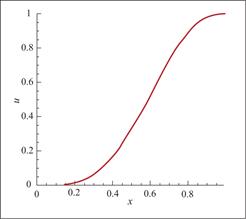
图2　函数在区间[0，1]上的示意图

Fig.2　Schematic representation of the function

on the interval [0，1]

元只需重构

(1.2.7)

(2)元

为单元的积分平均值，为单元的一阶矩，为单元的二阶矩，在模板上构造四次多项式满足

(1.2.8)

分别在模板，上构造二次多项式满足

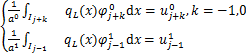(1.2.9)

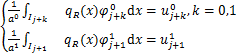(1.2.10)

我们的重构多项式为

(1.2.11)

计算对应的光滑因子

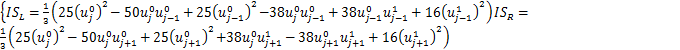(1.2.12)

的计算同元。

元时我们需要重构

(1.2.13)

(1.2.14)

(3)元

在模板上构造6次多项式满足

(1.2.15)

分别在模板上构造3次多项式满足

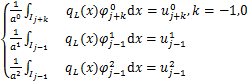(1.2.16)

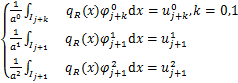(1.2.17)

我们所利用的重构多项式为

(1.2.18)

计算对应的光滑因子

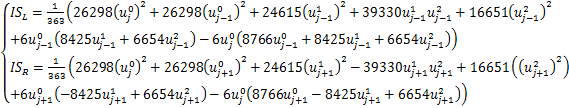(1.2.19)

，，，的计算同元。

元时我们需要重构，

(1.2.20)

(1.2.21)

(1.2.22)

1.3　时间离散

使用Runge-Kutta方法对半离散后得到的常微分方程组进行时间离散。令为的剖分，记，并且定义。

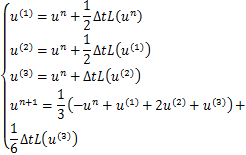
2　数值算例

2.1　算例1

(2.1.1)

我们计算到。表1~表6的计算结果验证了算例1在无限制器和基于HWENO限制器的间断型Petrov-Galerkin方法具有二阶、三阶和四阶精度。对比无限制器和基于HWENO限制器下的计算结果表明，DPG格式在基于HWENO限制器下的数值解没有使光滑区域极值点处降阶。

表1　基于线性元下算例1的误差的收敛阶(无限制器)

Table 1　Convergence order of the error of example 1 based on linear elements(without limiter)

N	L1error	L1order	error	order
10	1.16E-002	—	1.79E-002	—
20	3.03E-003	1.94	4.71E-003	1.93
40	7.69E-004	1.98	1.21E-003	1.96
80	1.93E-004	1.99	3.03E-004	2.00
160	4.83E-005	2.00	7.58E-005	2.00
320	1.21E-005	2.00	1.89E-005	2.00
640	3.00E-006	2.01	4.68E-006	2.01

表2　基于线性元下算例1的误差的收敛阶(HWENO限制器)

Table 2　Convergence order of the error of example 1 based on linear elements(HWENO limiter)

N
10	1.17E-002	—	3.36E-002	—
20	3.03E-003	1.95	6.25E-003	2.43
40	7.69E-004	1.98	1.21E-003	2.37
80	1.93E-004	1.99	3.03E-004	2.00
160	4.83E-005	2.00	7.58E-005	2.00
320	1.21E-005	2.00	1.89E-005	2.00
640	3.00E-006	2.01	4.68E-006	2.01

表3　基于二次元下算例1的误差的收敛阶(无限制器)

Table 3　Convergence order of the error of example 1 based on quadratic elements(without limiter)

N
10	5.34E-003	—	8.26E-003	—
20	6.47E-004	3.05	1.02E-003	3.02
40	8.03E-005	3.01	1.26E-004	3.02
80	1.00E-005	3.01	1.58E-005	3.00
160	1.25E-006	3.00	1.97E-006	3.00
320	1.57E-007	2.99	2.46E-007	3.00
640	1.96E-008	3.00	3.08E-008	3.00

表4　基于二次元下算例1的误差的收敛阶(HWENO 限制器)

Table 4　Convergence order of the error of example 1 based on quadratic elements(HWENO limiter)

N
10	5.34E-003	—	8.26E-003	—
20	6.47E-004	3.05	1.02E-003	3.02
40	8.03E-005	3.01	1.26E-004	3.02
80	1.00E-005	3.01	1.58E-005	3.00
160	1.25E-006	3.00	1.97E-006	3.00
320	1.57E-007	2.99	2.46E-007	3.00
640	1.96E-008	3.00	3.08E-008	3.00

表5　基于三次元下算例1的误差的收敛阶(无限制器)

Table 5　Convergence order of the error of example 1 based on cubic elements(without limiter)

N
10	4.15E-004	—	6.42E-004	—
20	2.12E-005	4.29	3.30E-005	4.28
40	1.61E-006	3.72	2.52E-006	3.71
80	9.42E-008	4.10	1.48E-007	4.09
160	5.48E-009	4.10	8.60E-009	4.11
320	3.46E-010	3.99	5.44E-010	3.98
640	2.13E-011	4.02	3.35E-011	4.02

表6　基于三次元下算例1的误差的收敛阶(HWENO限制器)

Table 6　Convergence order of the error of example 1 based on cubic elements(HWENO limiter)

N
10	4.15E-004	—	6.42E-004	—
20	2.12E-005	4.29	3.30E-005	4.28
40	1.61E-006	3.72	2.52E-006	3.71
80	9.42E-008	4.10	1.48E-007	4.09
160	5.48E-009	4.10	8.60E-009	4.11
320	3.46E-010	3.99	5.44E-010	3.98
640	2.13E-011	4.02	3.35E-011	4.02

2.2　算例2

(2.1.2)

2.3　算例3

(2.1.3)

为了区分不同剖分下图像的差别，图像只画出部分点。图3~图8给出了不同初值下T时刻时，，元的数值解和精确解的对比图。图像表明，基于HWENO限制器的间断型Petrov-Galerkin方法在计算Riemann初值问题时具有良好的效果，有效抑制虚假振荡，且随着求解区间加密和格式精度上升，数值解与精确解的吻合度越来越高。

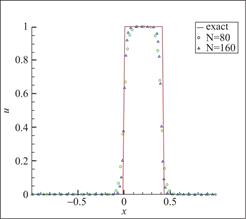
图3　算例2 P¹元，剖分80与160个单元，t=0.2

Fig.3　Schematic diagram of Example 2， 80 and 160 cells

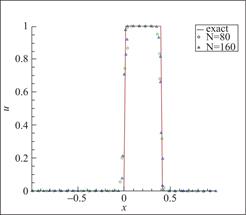
图4　算例2 P²元，剖分80与160个单元，t=0.2

Fig.4　Schematic diagram of Example 2， 80 and 160 cells

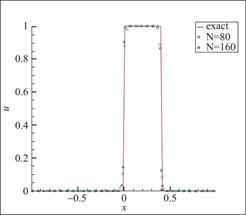
图5　算例2 P³元，剖分80与160个单元，t=0.2

Fig.5　Schematic diagram of Example 2， 80 and 160 cells

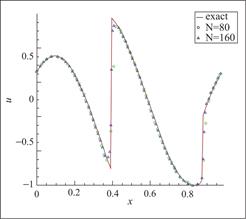
图6　算例3 P¹元，剖分80与160个单元，t=0.1

Fig.6　Schematic diagram of Example 3， 80 and 160 cells

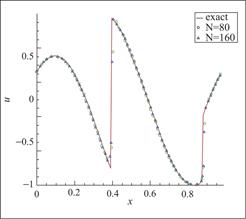
图7　算例3 P²元，剖分80与160个单元，t=0.1

Fig.7　Schematic diagram of Example 3， 80 and 160 cells

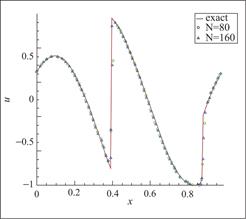
图8　算例3 P³元，剖分80与160个单元，t=0.1

Fig.8　Schematic diagram of Example 3， 80 and 160 cells

2.4　算例4

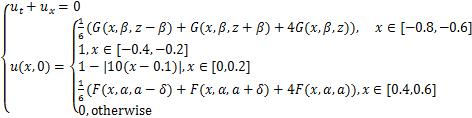(2.1.4)

初始条件包括高斯函数、一个方波、一个三角波和半个椭圆。图9~图11表明，该格式可以很好处理含有多种形式的间断问题，有效抑制非物理振荡。且随着求解区间加密和格式精度上升，数值计算结果与精确解的逼近程度更为良好。

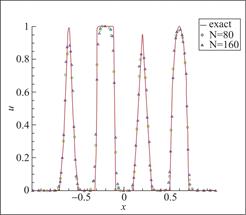
图9　算例4 P¹元，剖分80与160个单元，t=0.1

Fig.9　Schematic diagram of Example 4， 80 and 160 cells

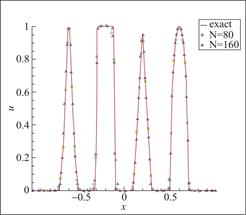
图10　算例4 P²元，剖分80与160个单元，t=0.1

Fig.10　Schematic diagram of Example 4， 80 and 160 cells

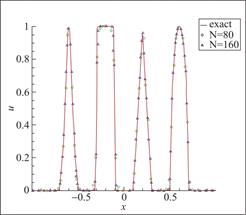
图11　算例4 P³元，剖分80与160个单元，t=0.1

Fig.11　Schematic diagram of Example 4， 80 and 160 cells

2.5　算例5 无黏Burgers方程

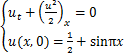(2.1.5)

由函数图像可知，Burgers方程在处出现间断解。图12~图14表明，该方法有效抑制了虚假振荡。对间断具有良好的分辨率。

图15为元下DG与DPG方法在N=80时的对比图，由图像可得与基于WENO限制器下的DG方法相比基于HWENO限制器下的DPG方法同样有较好的数值模拟效果。

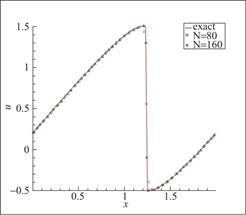
图12　算例5 P¹元，剖分80与160个单元，t=

Fig.12　Schematic diagram of Example 5， 80 and 160 cells

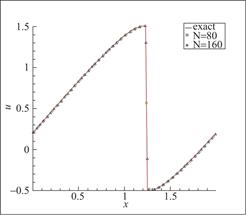
图13　算例5 P²元，剖分80与160个单元，t=

Fig.13　Schematic diagram of Example 5， 80 and 160 cells

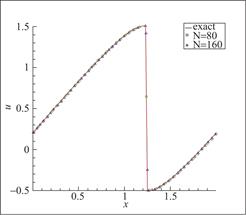
图14　算例5 P³元，剖分80与160个单元，t=

Fig.14　Schematic diagram of Example 5， 80 and 160 cells

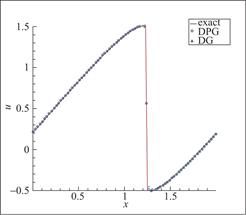
图15　算例5 P²元，DG与 DPG方法剖分80个单元， t=

Fig.15　Schematic diagram of Example 5，

DG and DPG methods， 80 cells

2.6　算例 6 一维Buckley-Leverett方程

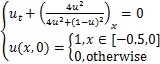(2.1.6)

由图16~图18可知，对比HWENO 限制器下的数值解与WENO格式^[23,24]下的数值解，验证了该格式数值解无振荡，可以很好地捕捉间断和激波，可以很好地近似精确解，具有高分辨率和低数值耗散性。

图19为元下DG与DPG方法在N=80时的对比图，由图像可得与基于WENO限制器下的DG方法相比基于HWENO限制器下的DPG方法可以很好地逼近间断解，有较好的数值模拟效果。

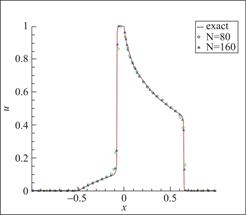
图16　算例6 P¹元，剖分80与160个单元，t=0.4

Fig.16　Schematic diagram of Example 6， 80 and 160 cells

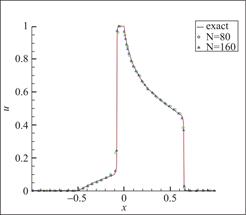
图17　算例6 P²元，剖分80与160个单元，t=0.4

Fig.17　Schematic diagram of Example 6，

80 and 160 cells

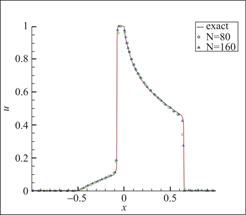
图18　算例6 P³元，剖分80与160个单元，t=0.4

Fig.18　Schematic diagram of Example 6，

80 and 160 cells

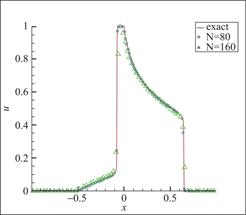
图19　算例6 P²元，DG与 DPG方法剖分80个单元，t=0.4

Fig.19　Schematic diagram of Example 6， DG and DPG methods， 80 cells

3　结论

本文研究了一维双曲守恒律方程基于HWENO限制器的间断型Petrov-Galerkin方法。在问题单元处，仅需一次重构，就可完成高阶矩的更新，且不需要计算线性权系数，降低了计算复杂程度。理论上该限制器的构造方法可用于任意次的DPG有限元方法，本文只给出元的计算结果。经典数值算例的计算结果表明，在保证紧致性的前提下，该限制器在捕捉激波间断方面有着不错的效果。在问题单元处有效抑制了虚假振荡，具有其理论设计的高精度和高分辨率特性。且随着格式精度的上升，可以很好地逼近间断解，具有良好的数值计算效果。

利益冲突: 作者声明无利益冲突。

---

^[①] *通讯作者　Corresponding author:高巍，gaow@imu.edu.cn
收稿日期:2022-10-21;　录用日期:2022-11-07;　发表日期:2023-06-28
基金项目:内蒙古大学科研发展基金(21100-5187133)，内蒙古自治区人才开发基金项目(12000-1300020240)。

参考文献(References)

[1] 水鸿寿. 一维流体力学差分方法[M]. 北京: 国防工业出版社, 1998.
[2] 刘儒勋, 舒其望. 计算流体力学的若干新方法[M]. 北 京: 科学出版社, 2003.
[3] 任玉新, 陈海昕. 计算流体力学基础[M]. 北京: 清华大学出版社, 2006.
[4] Reed W H, Hill T R. Triangular Mesh Methods for the Neutron Transport Equation[R]. Los Alamos National Laboratory, Los Alamos. 1973.
[5] Cockburn B, Shu C W. TVB Runge-Kutta local projection discontinuous galerkin finite element method for scalar conservation laws[J]. ESAIM: Mathematical Modelling and Numerical Analysis, 1991, 25: 337-361.
DOI:10.1051/M2AN/1991250303371
[6] Cockburn B, Shu, C. W. TVB Runge-Kutta local projection discontinuous galerkin finite element method for conservation laws II: General framework[J]. Mathematics of Computation, 1989, 52: 411-435.
DOI:10.1090/S0025-5718-1989-0983311-4
[7] Cockburn B, Lin S Y, Shu C W. TVB Runge-Kutta local projection discontinuous galerkin finite element method for conservation laws III: One-Dimensional systems[J]. Journal of Computational Physics, 1989, 84: 90-113.
DOI:10.1016/0021-9991(89)90183-6
[8] Cockburn B, Hou S, Shu C W. TVB Runge-Kutta local projection discontinuous galerkin finite element method for conservation laws IV: The multidimensional case[J]. Mathematics of Computation, 1990, 54: 545-581.
DOI:10.1090/S0025-5718-1990-1010597-0
[9] Cockburn B, Shu C W. The Runge-Kutta discontinuous galerkin method for conservation laws V: Multidimensional systems[J]. Journal of Computational Physics, 1998, 141: 199-224.
DOI:10.1006/JCPH.1998.5892
[10] Cockburn B, Shu C W. Runge-Kutta discontinuous galerkin methods for convection dominated problems[J]. Journal of Scientific Computing, 2001, 16: 173-261.
DOI:10.1023/A:1012873910884
[11] Bassi F, Rebay S. A high-order accurate discontinuous finite element method for the numerical solution of the compressible Navier-Stokes Equations[J]. Journal of Computational Physics, 1997, 131: 267-279.
DOI:10.1006/jcph.1996.5572
[12] Cockburn B, Shu C W. The local discontinuous galerkin finite element method for convection-diffusion systems [J]. SIAM Journal on Numerical Analysis, 1998, 35: 2440-2463.
DOI:10.1137/S0036142997316712
[13] 陈大伟. 求解双曲守恒律的龙格-库塔控制体积间断有限元方法(RKCVDFEM)[D]. 绵阳: 中国工程物理研究院, 2009.
[14] Zhao G Z, Yu X J, Guo P Y. The discontinuous Petrov- Galerkin Method for one-dimensional compressible Euler Equations in the Lagrangian Coordinate[J]. Chinese Physics B, 2013, 22: 100-107.
DOI:10.1088/1674-1056/22/5/050206
[15] 赵国忠, 蔚喜军, 郭怀民. 二维Lagrangian坐标系下可压气动方程组的间断Petrov-Galerkin方法(英文)[J]. 计算物理, 2017, 34(3): 294-308.
DOI:CNKI:SUN:JSWL.0.2017-03-006
[16] 赵国忠, 蔚喜军, 郭虹平, 等. 求解含有高阶导数偏微分方程的局部间断Petrov-Galerkin方法(英文)[J]. 计算物理, 2019, 36(5): 517-532.
DOI:10.19596/j.cnki.1001-246x.7919
[17] Qiu J, Shu C W. Runge-Kutta discontinuous galerkin method using WENO Limiters[J]. SIAM Journal on Scientific Computing, 2005, 26(3): 907-929.
DOI:10.1137/S1064827503425298
[18] Qiu J, Shu C W. Hermite WENO schemes and their application as limiters for Runge-Kutta Discontinuous Galerkin Method: One-Dimensional case[J]. Journal of Computational Physics, 2004, 193(1): 115-135.
DOI:10.1016/J.JCP.2003.07.026
[19] Qiu J, Shu C W. Hermite WENO schemes and their application as limiters for Runge-Kutta discontinuous galerkin method II: Two dimensional case[J]. Computers& Fluids, 2005, 34(6): 642-663.
DOI:10.1016/J.COMPFLUID.2004.05.005
[20] Xuan L, Wu J. A weighted-integral based scheme[J]. Journal of Computational Physics, 2010, 229(17): 5999- 6014.
DOI:10.1016/j.jcp.2010.04.031
[21] 房金伟. 间断有限元方法中限制器的研究[D]. 哈尔滨: 哈尔滨工业大学, 2011.
DOI:10.7666/d.D261109
[22] Gande N R, Rathod Y, Rathan S. Third-order WENO scheme with a new smoothness indicator[J]. International Journal for Numerical Methods in Fluids, 2017, 85(2): 90-112.
DOI:10.1002/fld.4374
[23] 孙阳, 李兴华, 艾晓辉. 新型紧致WENO5格式[J]. 哈尔滨理工大学学报, 2020, 25(1): 154-158.
DOI:10.15938/j.jhust.2020.01.024
[24] 阎超, 于剑, 徐晶磊, 等. CFD模拟方法的发展成就与展望[J]. 力学进展, 2011, 41(5): 562-589.

A Discontinuous Petrov-Galerkin Method for One-Dimensional Hyperbolic Conservation Law Equations Based on HWENO Limiter

DUAN Xiaofeng, GAO Wei^*

(School of Mathematical Sciences, Inner Mongolia University, Hohhot 010021, China)

Abstract: The discontinuous Petrov-Galerkin method (DPG) is a new type of numerical solution to the hyperbolic conservation law equations, which distinguishes itself from the DG method by its high accuracy based on compact stencils. However, in order to overcome the unphysical oscillations of the higher order linear schemes near the large gradient solution, the DPG method often needs to incorporate limiter functions to obtain a high-resolution image of the numerical solution. This paper attempts to combine HWENO as limiter function with DPG to solve the discontinuous initial value problems for the hyperbolic conservation law equations. The single-step high-accuracy SSP Runge-Kutta method is used for time discretization, and a new HWENO-based process is used as the limiter of the RKDPG methods, which requires only one reconstruction to complete the update of the higher-order moments without calculating the linear weight coefficients. . Since the accuracy does not meet the design requirements, the HWENO limiter above is partially improved for the identification of the problem cells in the HWENO limiter above, with the original numerical solution used at the smooth solution. This paper only gives the calculation results of P1 ~P3, and the limiter is also applicable to the DPG method for higher elements. Numerical examples show that the HWENO limiter can effectively suppress non-physical oscillations in the problem cells and keep the original accuracy at the non-problem cells. The high accuracy and compactness characteristics of the DPG method are maintained. The numerical calculation solutions are efficient and accurate.  

Keywords: Discontinuous Petrov-Galerkin Method, Hyperbolic Conservation Law, Hermite WENO Limiter, Runge-Kutta

DOI: 10.48014/fcpm.20221019002

Citation: DUAN Xiaofeng, GAO Wei. A discontinuous Petrov-Galerkin Method for one-dimensional hyperbolic conservation law equations based on HWENO Limiter[J]. Frontiers of Chinese Pure Mathematics, 2023, 1(1): 1-13.