一类具有病毒感染的随机传染病模型的平稳分布

郑亮

(兰州理工大学理学院, 兰州 730050)

摘要: 自2020年年初以来, 世界一直面临着以COVID-19大流行形式出现的最大的病毒学入侵, 而新冠病毒的爆发再次说明传染病仍然是人类生存和发展的最大威胁之一。因此在本文中, 研究了一类考虑环境病毒影响的随机COVID-19传染病SEIW (W为环境中病毒的浓度) 模型的平稳分布的存在性。首先, 通过构建合适的Lyapunov函数证明了系统解的存在性与唯一性。然后使用随机Lyapunov方法建立了参数Rs0, 并且证明了当Rs0>1时, 系统解在R4+上存在唯一的平稳分布。并且通过对比确定性模型的R0和随机性模型的Rs0, 可以发现Rs0受到白噪声的影响, 并且Rs0≤R0, 当σi→0 (i=1, 2, 3, 4) 时, Rs0→R0, 说明本文的工作是对确定性模型的一个扩展, 并且当随机扰动较小时, 系统解在R4+上存在唯一的平稳分布。

关键词: 病毒感染, 随机传染病模型, 平稳分布

DOI: 10.48014/fcpm.20230515001

引用格式: 郑亮. 一类具有病毒感染的随机传染病模型的平稳分布[J]. 中国理论数学前沿, 2023, 1(1): 21-30.

文章类型: 研究性论文

收稿日期: 2023-05-15

接收日期: 2023-05-22

出版日期: 2023-06-28

0　引言

数学模型是研究传染病传播方式和描述传染病对人类生活影响的重要工具。通过建立数学模型，可以了解疾病的动态行为，并提供一些控制其传播的措施。Zhou等^[1]研究了疫情早期媒体报道对缓解COVID-19传播的影响，他们发现提高媒体对COVID-19疫情严重程度报道的反应率可以使感染高峰提前和减小感染高峰规模。Debadatta等^[2]运用确定性和随机性SLIR模型来预测COVID-19在西班牙的传播动态，其中L表示潜伏期。Bai和Wang ^[3]将病原体纳入环境，研究了一个具有两个斑块结构的COVID-19传染病模型。

在Bai和Wang^[3]的基础上，我们仅考虑一个斑块结构的COVID-19传染病模型如下:

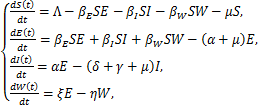(1.1)

式中，S(t)表示易感者，E(t)表示潜伏者，I(t)表示感染者，W(t)表示环境中病毒浓度，Λ表示出生率，β_E表示易感者与潜伏者的感染率，β_I表示易感者与感染者的感染率，β_W表示易感者与环境中病原体的感染率，μ表示自然死亡率，表示平均潜伏时间，δ表示因病死亡率，γ表示感染者的恢复率，ξ表示潜伏者向环境输入病毒的速率，η表示病毒在环境中的消亡速率。

显然，系统(1.1)的无病平衡点x₀=(S₀，0，0，0)=，地方病平衡点x₁=(S₁，E₁，I₁，W₁)，其中，S₁=，E₁=，I₁=，W₁=。然后根据下一代矩阵方法^[4]可以得到基本再生数

R₀=.

在文献^[3]中，他们证明了当R₀<1时，系统(1.1)的无病平衡点是全局渐进稳定的;当R₀>1时，系统(1.1)的地方病平衡点是全局渐进稳定的。

在实际生活中，由于真实环境是不确定的和随机的，出生率、承载能力、竞争系数和其他表征自然生物系统的参数都或多或少地表现出随机波动。许多文献都表明环境的随机波动对传染病模型动力学行为存在影响。例如，Gray等^[5]建立了一类随机SIS传染病模型，发现噪声强度的增大会抑制疾病的流行，这一结论在文献^[6]中也被得到。Zhao等^[7]建立了一类具有疫苗接种的随机SIS传染病模型，发现当噪声比较小时，阈值参数能确定疾病的灭绝和持久。Dieu^[8]建立了一类具有Beddington-DeAngelis功能反应函数的随机SIR传染病模型，通过证明边界方程存在平稳分布进一步得到阈值，从而得到了疾病灭绝和持久的充分几乎必要条件。Li等^[9]研究了一类受环境扰动的肿瘤-免疫系统的动力学行为，他们构建了随机Lyapunov函数、运用随机微分方程的比较原理和强遍历性原理，证明了系统正解的存在性、有界性，得到了肿瘤免疫系统的平稳分布的存在唯一性和疾病的随机持久性。此外，还有许多学者也研究了受到环境噪声影响的传染病模型^[10-16]。

在系统(1.1)的基础上，假设随机波动为白噪声类型，与变量S，E，I，W成正比。因此对应于系统(1.1)的随机版本具有如下形式:

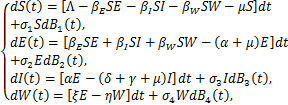(1.2)

其中，B_i(t)(i=1，2，3，4)表示相互独立的标准布朗运动，(i=1，2，3，4)表示随机扰动强度。

在本文中，除非另有说明，否则设(Ω，F，，P)是一个完全概率空间，其中满足通常条件(即它是右连续的，且包含所有P-null集)。记a∧b=min{a，b}和a∨b=max{a，b}。

设x(t)(t≥0)是Itô过程，并且满足下面的随机微分

dx(t)=f(t)dt+g(t)dB(t)，

其中，f∈L¹，g∈L²。令V(x，t)∈C^2,1，则V(x(t)，t)仍是It过程，其随机微分具有如下形式

dV(x(t)，t)=LV(x，t)dt+V_x(x，t)g(t)dB(t)a.s.

其中，

LV(x，t)=V_t(x，t)+V_x(x，t)f(t)
+trace，

称上式为Itô's公式。

文章剩余内容如下。在第1小节中，证明了系统(1.2)在上全局正解的存在唯一性。在第2小节中，首先构造了决定疾病持久的参数，然后通过构造合适的Lyapunov函数来证明，当>1时，系统在上存在唯一的平稳分布π(·)。第3小节对本文主要结论进行了总结。

1　全局正解的存在唯一性

这一节，我们利用Lyapunov方法来分析模型(1.2)解的存在唯一性。首先，定义={x=(x₁，x₂，x₃，x₄)∈:x_i>0，i=1，2，3，4}。下面将证明模型(1.2)的解保持在中的概率为1。

定理2.1　对任意给定的初始值(S(0)，E(0)，I(0)，W(0))∈，系统(1.2)在t≥0上存在唯一的解(S(t)，E(t)，I(t)，W(t))，且解(S(t)，E(t)，I(t)，W(t))在中的概率为1，即对任意的t≥0，有(S(t)，E(t)，I(t)，W(t))∈a.s.。

证明　由于模型(1.2)的系数是局部Lipschitz连续的，则对任意的初值(S(0)，E(0)，I(0)，W(0))∈和t∈，模型(1.2)存在唯一的局部解，其中τ_e表示爆破时间。要证解是全局的，只需证明τ_e=¥ a.s.令k₀>1，使得(S(0)，E(0)，I(0)，W(0))在区间。对于任意的整数k≥k₀，定义停时:

τ_k=inft∈:S(t)∉或E(t)∉或I(t)∉或W(t)∉，本文中，令infØ=¥。

显然，当k→¥时，τ_e是单增的。记=τ_k，则≤τ_e a.s.。如果=¥ a.s.，那么τ_e=¥ a.s.。下面运用反证法证明=¥。设≠¥，则存在T>0和任意的􀆠∈(0，1)使得

P>􀆠.

因此存在整数k₁≥k₀使得

P≥􀆠，k≥k₁，

其中，Ω_k=。

考虑C²-函数V:→R，V(S，E，I，W)=S-a-aln+E-1-lnE+I-1-lnI+W-1-lnW，其中a是待定常数。令k≥k₀和T是任意的。使用Itô's公式，得到

dV(S，E，I，W)=LV(S，E，I，W)dt
+σ₁(S-a)dB₁(t)
+σ₂(E-1)dB₂(t)
+σ₃(I-1)dB₃(t)
+σ₄(W-1)dB₄(t)

其中，

LV(S，E，I，W)=(Λ-β_ESE-β_ISI-β_WSW

-μS)++[β_ESE

+β_ISI+β_WSW-(α+μ)E]

++[αE-(δ+γ

+μ)I]++(ξE

-ηW)+

≤Λ-μS+E

+I

+W-

+

+

+，

令a=max>0，故aβ_E+ξ-μ，aβ_I-(δ+γ+μ)，aβ_W-η≤0。因此

dV≤Λ-μS-+a+

++dt

+σ₁(S-a)dB₁(t)+σ₂(E-1)dB₂(t)

+σ₃(I-1)dB₃(t)+σ₄(W-1)dB₄(t)

≤Λ+a+

++dt

+σ₁(S-a)dB₁(t)+σ₂(E-1)dB₂(t)

+σ₃(I-1)dB₃(t)+σ₄(W-1)dB₄(t)

=Mdt+σ₁(S-a)dB₁(t)+σ₂(E-1)dB₂(t)

+σ₃(I-1)dB₃(t)+σ₄(W-1)dB₄(t)，

其中，M=Λ+a+++。因此对于任意的k≥k₁，得到

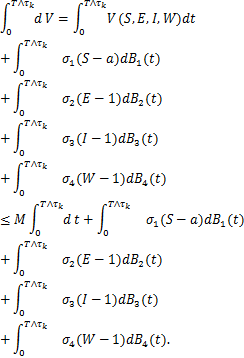
则

令Ω_k=，显然有P≥ε。对∀ω∈Ω_k，可知S(τ_k，ω)，E(τ_k，ω)，I(τ_k，ω)，W(τ_k，ω)至少有一个等于k或。则

V(S(τ_k，ω)，E(τ_k，ω)，I(τ_k，ω)，W(τ_k，ω))

　≥mink-a-aln，-a+lnak，k-1

-lnk，-1-ln

:=h(k).

所以

V(S(0)，E(0)，I(0)，W(0))+MT

　≥EV(S(τ_k，ω)，E(τ_k，ω)，I(τ_k，ω)，W(τ_k，ω))

≥E[(ω)V(S(τ_k，ω)，E(τ_k，ω)，I(τ_k，ω)，

W(τ_k，ω))]

≥εh(k).

令k→¥，可知¥>V(S(0)，E(0)，I(0)，W(0))+MT=¥，显然矛盾。因此=¥。

2　平稳分布的存在性

在这一部分中，将证明系统(1.2)在上存在平稳分布的充分条件。首先给出将要用到的引理。

引理3.1　([17])如果存在一个具有正则边界的有界开域U∈，使得以下条件成立:

(i)在定义域U及其邻域内，扩散矩阵A(x)的最小特征值非零。

(ii)对任意的x∈U，从x出发到达U的平均时间τ是有限的，且对每个紧子集K⊂满足sup_x∈KE^xτ<¥。

那么马尔科夫过程X(t)有唯一的平稳分布π(·)。

定理3.1　假设

:=

×>1，

那么对任意的初值(S(0)，E(0)，I(0)，W(0))∈，系统在上存在一个唯一的平稳分布π(·)。

证明　为了证明定理3.1，仅需要证明引理3.1的条件(i)和(ii)均成立即可。首先证明条件(i)。可以得到系统(1.2)的扩散矩阵

A=.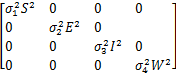

显然，矩阵A对于的任意紧子集都是正定的，因此引理3.1的条件(i)成立。

下面，将证明引理3.1的条件(ii)。定义

V₁(S，E，I，W)=-lnE(t)-a₁lnI(t)　　　　

-a₂lnW(t)-a₃lnS(t)

-a₄lnS(t)-a₅lnS(t)，

其中a₁，a₂，a₃，a₄和a₅均为待定正常数。使用Itô's公式，得到

LV₁=-β_ES-β_I-β_W

+-a₁α

+a₁

-a₂ξ+a₂

--β_EE-β_II-β_WW

-

≤-2+

+a₃-3

+a₁

+a₄-3

+a₂+a₅

+. (3.1)

令

a₁=，

a₂=，

a₃=，
a₄=，
a₅=，(3.2)

并将a₁，a₂，a₃，a₄和a₅代入(3.1)，进一步得到

LV₁≤

--

-

+

=-

+， (3.2)

其中，

=

.

接下来，定义V₂(S，E，I，W)=V₁(S，E，I，W)+I+W，根据(3.2)式，得到

　LV₂≤-

+E.

定义V₃(S，I，W)=-lnS-lnI-lnW，V₄(S，E，I，W)=(S+E+I+W)^θ+1，其中θ充分小且0<θ<。根据Itô's公式，得到

LV₃=-+β_EE+β_II+β_WW

-α-ξ

+ (3.3)

且

LV₄=Λ-μS-E

-I-W

+S²+E²

+I²+W²

≤Λ-S+E

+I+W+S+E+I

+W^θ+1

=Λ

--S+E

+I+W^θ+1

≤B--

≤B--

， (3.4)

其中，B=Λ-(μ∧η)-(∨∨∨)(S+E+<¥。

定义一个C²-函数V:→R，V(S，E，I，W)=KV₂(S，E，I，W)+V₃(S，I，W)+V₄(S，E，I，W)，其中K是充分大的一个正常数且满足

-K+C≤-2，(3.5)

其中，

C=-

+β_EE+β_II+β_WW+B

+. (3.6)

此外，注意到V(S，E，I，W)在上是连续的，并且当(S，E，I，W)趋向于0或+¥时，均有V(S，E，I，W)=+¥。因此V(S，E，I，W)在内部可以取到最小值，不妨设最小值点为(S⁰，E⁰，I⁰，W⁰)。那么设C²-函数V:→，

V=KV₂+V₃

+V₄

-V.

根据(3.1)，(3.2)，(3.3)和(3.4)，可以得到

LV≤-K

+KE

--α-ξ+β_EE+β_II+β_WW

+

+B-

≤-K

+KE

--α-ξ

-

-

+β_EE+β_II+β_WW+B

+. (3.7)

下面，证明引理3.1中的条件(2)成立，首先定义一个有界开域

U_􀆠=，

其中，0<􀆠<1且充分小。在集合U_􀆠中，为了证明引理3.1中的条件(ii)成立，因此选择充分小的􀆠使得以下式子成立

-+D≤-1，(3.8)

K􀆠≤1，(3.9)

-+D≤-1(3.10)

-+D≤-1(3.11)

-+D≤-1，(3.12)

-+D≤-1，(3.13)

-
+D≤-1，(3.14)

其中，

D=-(μ∧η)

　-E^θ+1+I^θ+1

　+W^θ+1

　+KE

　+β_EE+β_II+β_WW

　+B+.

将U_􀆠划分成8个区域，

U₁=，

U₂=，

U₃=，

U₄=，

U₅=，

U₆=，

U₇=，

U₈=，

并且容易看出U_􀆠=U₁∪U₂∪U₃∪U₄∪U₅∪U₆∪U₇∪U₈。下面将证明对任意的(S，E，I，W)∈U_􀆠有LV≤-1成立，即证明在上述8个区域中，均有LV≤-1成立。

(1)对任意的(S，E，I，W)∈U₁，根据式(3.7)和(3.8)，有

LV≤---

+KE

+β_EE+β_II+β_WW

+B+

≤-+D

≤-1. (3.15)

(2)对任意的(S，E，I，W)∈U₂，根据式(3.7)和(3.9)，有

LV≤-K+K

E

--

+β_EE+β_II+β_WW+B

+

≤-K+K(a₃+a₄

+a₅)􀆠+C

≤-1 (3.16)

(3)对任意的(S，E，I，W)∈U₃，根据式(3.7)和(3.10)，有

LV≤-α-

+KE

+β_EE+β_II+β_WW

+B+

≤-α+D

≤-1. (3.17)

(4)对任意的(S，E，I，W)∈U₄，根据式(3.7)和(3.11)，有

LV≤-ξ-

+KE

+β_EE+β_II+β_WW

+B+

≤-ξ+D

≤-1. (3.18)

(5)对任意的(S，E，I，W)∈U₅，根据式(3.7)和(3.12)，有

LV≤-S^θ+1　

+KE

+β_EE+β_II+β_WW

-

+B+δ+γ+2μ+η+

≤-+D

≤-1 (3.19)

(6)对任意的(S，E，I，W)∈U₅，根据式(3.7)和(3.12)，有

LV≤-E^θ+1

+KE

+β_EE+β_II+β_WW

-

+B+

≤-+D

≤-1. (3.20)

(7)对任意的(S，E，I，W)∈U₅，根据式(3.7)和(3.13)，有

LV≤-I^θ+1+

KE

+β_EE+β_II+β_WW

-

+B+

≤-+D

≤-1 (3.21)

(8)对任意的(S，E，I，W)∈U₅，根据式(3.7)和(3.14)，有

LV≤-

+K

+β_EE+β_II+β_WW

-

+B+

≤-

+D

≤-1 (3.22)

因此，根据式(3.15)~(3.22)，对充分小的􀆠使得当(S，E，I，W)∈U_e时，均有

LV≤-1.(3.23)

所以引理3.1的条件(ii)成立。根据引理3.1，系统(1.2)在上存在唯一的平稳分布π(·)。定理3.1证明完成。

注3.1　通过对比确定性模型的R₀和随机模型的，发现<R₀，且当σ_i→0(i=1，2，3，4)时，→R₀，说明所得的结果是对确定性模型相关工作的一个扩展，并且当扰动较小时，随机模型在上存在一个唯一的平稳分布π(·)。

3　结论

本文研究了一类具有病毒感染的随机传染病模型的平稳分布。通过使用随机Lyapunov方法建立参数，证明了当>1时，系统解在上存在唯一的平稳分布，并且通过对比确定性模型的R₀和随机模型的，可以发现≤R₀，当σ_i→0(i=1，2，3，4)时，→R₀，说明当扰动较小时，随机模型在上存在一个唯一的平稳分布，这一结果是对确定性模型相关工作的一个扩展。

本文所研究的内容并不完整，有许多问题值得进一步讨论。例如，未证明疾病灭绝的充分条件。此外，本文仅仅研究了由白噪声描述的连续随机扰动，而实际生活中仍有许多不连续的随机扰动是不能用白噪声来模拟的，如电报噪声和Ley噪声。

利益冲突: 作者声明无利益冲突。

---

^[③] 通讯作者　Corresponding author:郑亮，983611698@qq.com
收稿日期:2023-05-15;　录用日期:2023-05-22;　发表日期:2023-06-28

参考文献(References)

[1] ZHOU W K, WANG A L, XIA F, et al. Effects of media reporting on mitigating spread of COVID-19 in the early phase of the outbreak[J]. Mathematical Biosciences and Engineering, 2020, 17(3): 2693-2707.
https://doi.org/10.3934/mbe.2020147
[2] ADAK D, MAJUMDER A, BAIRAGI N. Mathematical perspective of COVID-19 pandemic: Disease extinction criteria in deterministic and stochastic models[J]. Chaos, Soli-tons & Fractals, 2021, 142: 110381.
https://doi.org/10.1101/2020.10.12.20211201
[3] BAI J, WANG J. A two-patch model for the COVID-19 transmission dynamics in China[J]. Journal of Applied Analysis and Computation, 2021, 11(4): 1982-2016.
https://doi.org/10.11948/20200302
[4] VAN DEN DRIESSCHE P, WATMOUGH J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission[J]. Mathematical Biosciences, 2002, 180(1-2): 29-48.
https://doi.org/10.1016/S0025-5564(02)00108-6
[5] GRAY A, GREENHALGH D, HU L L, et al. A stochastic differential equation SIS epidemic model[J]. SIAM Journal on Applied Mathematics, 2011, 71(3): 876-902.
https://doi.org/10.1137/10081856X
[6] CAI Y L, KANG Y, BANERJEE M, et al. A stochastic SIRS epidemic model with infectious force under intervention strategies[J]. Journal of Differential Equations, 2015, 259(12): 7463-7502.
https://doi.org/10.1016/j.jde.2015.08.024
[7] ZHAO D L, ZHANG T S, YUAN S L. The threshold of a stochastic SIVS epidemic model with nonlinear saturated incidence[J]. Physica A: Statistical Mechanics and its Applications, 2016, 443: 372-379.
https://doi.org/10.1016/j.physa.2015.09.092
[8] DIEU N T. Asymptotic properties of a stochastic SIR epidemic model with Beddington-Deangelis incidence rate[J]. Journal of Dynamics and Differential Equations, 2018, 30: 93-106.
https://doi.org/10.1007/s10884-016-9532-8
[9] LI X Y, SONG G T, XIA Y, et al. Dynamical behaviors of the tumor-immune system in a stochastic environment[J]. SIAM Journal on Applied Mathematics, 2019, 79(6): 2193-2217.
https://doi.org/10.1137/19M1243580
[10] JI C Y, JIANG D Q. Threshold behaviour of a stochastic sir model[J]. Applied Mathematical Modelling, 2014, 38(21-22): 5067-5079.
https://doi.org/10.1016/j.apm.2014.03.037
[11] ZHOU Y L, ZHANG W G, YUAN S L. Survival and stationary distribution of a SIR epidemic model with stochastic perturbations[J]. Applied Mathematics and Computation, 2014, 244: 118-131.
https://doi.org/10.1016/j.amc.2014.06.100
[12] LAHROUZ A, OMARI L, KIOUACH D. Global analysis of a deterministic and stochastic nonlinear SIRS epidemic model[J], Nonlinear Analysis: Modelling and Control, 2011, 16(1): 59-76.
https://doi.org/10.15388/NA.16.1.14115
[13] DIEU N T, NGUYEN D H, DU N H, et al. Classification of asymptotic behavior in a stochastic SIR model[J]. SIAM Journal on Applied Dynamical Systems, 2016, 15(2): 1062-1084.
https://doi.org/10.1137/15M1043315
[14] NGUYEN D N, YIN G, ZHU C. Long-term analysis of a stochastic SIRS model with general incidence rates[J]. SIAM Journal on Applied Mathematics, 2020, 80(2): 814-838.
https://doi.org/10.1137/19M1246973
[15] DU N H, NHU N N. Permanence and extinction for the stochastic SIR epidemic model[J]. Journal of Differential Equations, 2020, 269(11): 9619-9652.
https://doi.org/10.1016/j.jde.2020.06.049
[16] DU N H, DIEU N T, KY T Q, et al. Long-time behavior of a stochastic SIQR model with markov switching[J]. Acta Mathematica Vietnamica, 2020, 45: 903-915.
https://doi.org/10.1007/s40306-020-00376-0
[17] KHASMINSKII R. Stochastic Stability of Differential Equations[M]. Sijthoff & Noord-hoff, 1980.
https://doi.org/10.1007/978-3-642-23280-0

Stationary Distribution of a Random Epidemic Model with Virus Infection

ZHENG Liang

(Lanzhou University of Technology, School of Science, Lanzhou 730050, China)

Abstract: Abstract: Since the beginning of 2020 the world has been facing the largest virological invasion in the form. of the COVID-19 pandemic, and the outbreak of COVID-19 has once again demonstrated that infectious diseases remain one of the greatest threats to human survival and development. In this paper, therefore, the existence of a stationary distribution for a class of stochastic COVID-19 infectious disease SEIW (W is the concentration of virus in the environment) models that take into account the effect of environmental viruses is investigated. First, the existence and uniqueness of the solution of the system are proved by constructing a suitable Lyapunov function. The parameters Rs0 are then established using the stochastic Lyapunov method and the existence of a unique stationary distribution of the system solution on R4+ when Rs0 >1 is demonstrated. And by comparing the deterministic model of R0 and the stochastic model of Rs0 , it can be found that Rs0 is influenced by white noise and Rs0 ≤R0, when σi →0 (i=1, 2, 3, 4) , Rs0 →R0, indicating that the work in this paper is an extension of the deterministic model and when the random perturbations are small, there exists a unique stationary distribution on R4+ for the system solution.  

Keywords: Virus infection, stochastic infectious disease model, stationary distribution

DOI: 10.48014/fcpm.20230515001

Citation: ZHENG Liang. Stationary distribution of a random epidemic model with virus infection[J]. Frontiers of Chinese Pure Mathematics, 2023, 1(1): 21-30.