基于lq正则项的稀疏线性判别分析-HTML全文-中国理论数学前沿-科学足迹出版社(SFP)

基于lq正则项的稀疏线性判别分析

陈静, 高彩霞^*

(内蒙古大学数学科学学院, 呼和浩特 010021)

摘要: 线性判别分析在特征提取和数据降维及分类上具有重要的作用, 随着科技的进步, 需要处理的数据越来越庞大, 然而在高维情形下, 线性判别分析面对着两个问题—投影后的数据解释性不足, 因为它们均涉及到所有p个特征, 是所有特征的线性组合以及类内协方差矩阵的奇异性问题。线性判别分析存在三个不同的论点: 多元高斯模型、Fisher判别问题和最优评分问题。针对这两个问题, 本文建立了一种求解第k个判别成分的模型, 该模型首先对线性判别分析中的Fisher判别问题原始模型做出变换, 利用类内方差的对角估计矩阵代替原始类内协方差矩阵, 克服了矩阵奇异的问题, 同时将其投影到正交投影空间上, 以便去掉其正交约束, 随后加入了lq范数正则项, 增强其解释性, 实现降维和分类的目的。最后给出了求解该模型的迭代算法及收敛性分析, 证明了由该算法产生的序列是下降收敛的, 且对任意初始值均收敛到问题的局部最小值。

关键词: 线性判别分析, 稀疏优化, lq 范数, 投影

DOI: 10.48014/fcpm.20230529001

引用格式: 陈静, 高彩霞. 基于lq 正则项的稀疏线性判别分析[J]. 中国理论数学前沿, 2023, 1(2): 31-38.

文章类型: 研究性论文

收稿日期: 2023-05-29

接收日期: 2023-06-21

出版日期: 2023-09-28

0　引言

模式分类是模式识别的核心研究内容，它可以分为有监督学习和无监督学习。有监督学习需要已知每个数据点所属的类别或标签作为输入，并通过训练来建立一个分类模型，使其能够正确地预测新数据点的类别或标签。无监督学习则不需要提供标签信息，而是寻找数据中的内在结构并将数据分组到不同的簇中。分类算法是模式分类的核心部分之一，常见的分类算法包括决策树、朴素贝叶斯、支持向量机、神经网络等。

近年来受到广泛关注的特征选择和提取在模式分类中发挥着重要作用。然而，图像原始数据包含大量冗余特征和噪声，给图像识别和图像分析带来了困难^[1^]。在这种情况下，对于分类任务，如何选择和提取整个练习中最重要的特征的不同类别是最重要的，也是最难的。事实证明，特征选择和提取是机器学习和模式分类领域的有效工具。它们可以降低复杂性，提高效率并增强分类性能^[2^]。

在过去的几十年中，人们提出了各种特征提取方法。在这个分支中，主成分分析(PCA)是最著名的方法之一，其主要思想是尝试学习一个可以保留原始数据主要能量的投影^[3^]。局部保留投影(LPP)，稀疏保留投影(SPP)和邻域保留嵌入(NPE)，他们学习的投影也是特征提取方法，这些方法考虑了原始的局部流形几何数据并尝试在投影空间中保留局部信息。随后，分类器，例如K最近邻(KNN)和支持向量机(SVM)，通常用于分类。上述方法虽然没有使用数据的标签信息，各有优势，但在一定程度上这些算法的分类性能还不够好。

实际上，我们希望对带有类别标签的数据(有监督的)可以实现降维，降维后可以更好地区分每个类别。这时，出现了另一种经典的特征提取算法—线性判别分析(LDA)。然而在高维情形下，从LDA得到的分类规则缺乏解释性，因此，为获得稀疏的判别变量，本文将在LDA中引入范数正则项。

1　预备知识

1.1　符号与定义

，其中表示向量或矩阵的转置，表示维实数向量的全体。是一个数据矩阵，其中表示维实数矩阵的全体。表示矩阵的第行第列元素。Tr(X)表示矩阵X的迹，即主对角线上各元素之和，表示矩阵X的秩，表示矩阵X的协方差矩阵。广义实数集可表示为。

1.2　文献综述

线性判别分析(Linear discriminant analysis)因其简单、稳健和预测准确性而成为许多应用中监督分类的首选工具^[4^]。LDA还提供数据在最具辨别力的方向上的低维投影，这对于数据解释很有用。LDA分类器存在三个不同的论点:多元高斯模型、Fisher判别问题和最优评分问题。经典LDA通常在简单和低维数据集上具有优异的性能。但已知它存在两个问题:

(1)当预测变量的数量大于观察值时。在这种情况下，不能直接应用LDA，因为特征的类内协方差矩阵是奇异的^[5^]。

(2)当较大时，从LDA得到的分类规则很难解释，因为它涉及所有特征，是所有特征的线性组合。

在某些情况下，人们可能希望有一个执行特征选择的分类器。这种稀疏分类器确保更容易的模型解释，并可以减少训练数据的过度拟合。

Fisher LDA通过最大化类间方差和类内方差之间的样本比率来寻找一组判别向量。为解决特征的类内协方差矩阵奇异这一问题，Krzanowski等^[6^]考虑了类内协方差矩阵的其他正定估计。Guo、Hastie 和Tibshirani等^[7^]在萎缩质心正则化判别分析(RDA)中，估计协方差矩阵时结合了脊型罚和软阈值。

为获得稀疏判别向量，受Zou等^[8^]提出的稀疏PCA方法启发，Qiao等^[9^]提出了针对高维低样本数据的稀疏线性判别分析。首先通过将广义特征值问题转换为回归类型问题，将判别向量与回归系数向量相关联，然后应用具有惩罚的惩罚最小二乘法来解决问题。2011年Witten等^[10^]在其文献中同样将惩罚应用于Fisher判别问题，解决该问题是具有挑战性的，因为它不是凸问题，因此必须应用专门的技术，如文中所提出的最小化最大化方法。同年，Shao等^[11^]提出了基于高维数据阈值的稀疏线性判别分析，证明了其在未知参数的某些稀疏条件下渐近最优。文章中还表明，当样本数时，Fisher线性判别是渐近最优的。但是当变量维数远大于时，Fisher判别准则的错判概率接近，也就是说此时线性判别分析相当于随机猜测。

作为LDA的一种等价形式，开发了最优评分，这在Hastie、Buja和Tibshirani的文章中进行了详细讨论^[12^]。它是通过一系列评分，将分数分配给类别(组、类别)，将分类变量转换为定量变量，从而将分类问题重铸为回归问题。对于二值分类，Mai和Zou^[21^]建立了Fisher判别问题和最优评分问题之间的等价性，并声明它们都按照缩放正则化参数的贝叶斯规则进行求解。最优评分标准的形式为:

s.t　Y^TYθ_k=1，

Y^TYθ_l=0.(1≤l≤k-1)

式中，X是一个n×p数据矩阵，在行上具有观察值，在列上具有特征，Y表示k类伪变量的n×k矩阵，Y_ik是第i个观测值是否属于第k类的指标变量，如果第i个观测值属于第k类，则由Y_ij=1定义，否则有Y_ij=0。由于X的列居中，平均值为零^[13^]。一些研究人员提出通过对β_k施加惩罚来惩罚最优得分标准。

2　模型

2.1　模型介绍

下面介绍Fisher线性判别分析(FLDA或LDA)的相关定义和模型，FLDA目的是寻找一个使得类间平方和与类内平方和的比率最大化的线性函数a^Tx，形式上，假设有k个类别，并设x_ij，j=1，…，n_i，i=1，…，k，表示第i类观测值的向量。x_i表示第i类的平均值，n=n₁+…+n_k，令X是一个n×p数据矩阵，且y=Xa，则FLDA求解:

式中，表示y的第i个子向量y_i的均值，对应于第i个类别。用Xa代替y，我们可以将类内平方和重写为:

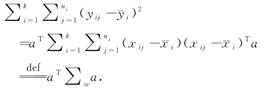
类间平方和为:

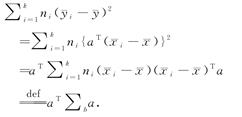
因此，比率可以由下式给出:

如果a₁是使比率最大化的向量，则可以找到在中与a₁正交的下一个方向a₂，使得比率最大化，并且可以类似地依次计算附加方向。投影方向a_i通常称为判别坐标，线性函数x称为Fisher线性判别函数。

2.2　模型发展

下面介绍稀疏LDA的模型发展，LDA的主要思想是投影，该算法的优点是缩短了同类型样本的投影距离，同时也可以增加不同类型的样本的距离。但是LDA也有它的设计缺陷。它的大部分投影系数不为零，新的特征样本是所有样本特征的线性组合，导致投影后的矩阵对特征缺乏很好的解释性，体现在以下几个方面。首先，LDA对矩阵特征没有很好的解释，无法在大量冗余数据中选择最合适的函数。其次，鲁棒性较差，LDA选择前k个最小特征值对应的k个特征向量作为特征提取投影时，受数据影响较大，LDA数据分类变化较大。这导致对于不同大小的数据集，LDA的分类准确率存在很大差异。针对这些问题，众多研究者提供了解决方法。例如，一种获得稀疏判别变量的方法是利用l₁惩罚，其优化问题为:

Witten和Tibshirani在文献[10]中采用了这种方法，并采取最小化—最大化方法求解该模型。

2022年束磊等^[14^]将l₀惩罚用于原始模型上，提出了基于l₀约束的稀疏线性判别分析模型如下:

式中，是类内协方差矩阵的对角阵估计，是利用正交投影思想转化后的类间协方差矩阵，s是事先给定的稀疏度。文中给出了一种稀疏LDA算法进行求解，在实验效果上说明了其收敛性，但并未证明。

Line Vlemmensen等^[5^]转而应用l₁惩罚到 LDA的最佳得分公式中。文中的SDA方法是按顺序定义的。第k个SDA解对(θ_k，β_k)求解问题:

　‖Yθ_k-Xβ_k‖+rΩβ_k+λ‖β_k‖₁

s.t. Y^TYθ_k=1，

Y^TYθ_l=0　(1<l≤k-1)

式中，λ为非负调谐参数，Ω为正定惩罚矩阵。如果对于r>0，Ω=rI那么这是一个弹性净罚。如果r足够大，则生成的判别向量将是稀疏的。如果r=0，那么这就简化为Hastie等^[5^]提出的惩罚判别分析。上式可以用一种简单的迭代方式进行优化:我们对β_k保持固定θ_k进行优化，我们对θ_k保持β_k固定进行优化。

在文献[15]中，Le Thi等将l₀正则化项添加到最优评分的目标函数以赋予判别向量稀疏性，提出l₀稀疏最优评分问题，其公式如下:

　‖Yθ_k-Xβ_k‖+λ₁‖β_k+λ₂‖β_k‖₀

s.t. Y^TYθ_k=1，

Y^TYθ_l=0　(1<l≤k-1)

文中提出了一种基于DC(凸函数差分)规划方法的新BCD方法。为了处理l₀正则化项，使用两个非凸连续函数来近似l₀范数。然后通过进行DC分解，利用直流算法解决最小化l₀的子问题。然而，在DC方案中，需要解决一系列非光滑子问题。这将增加新提出的坐标下降法的计算负担。

在线性判别分析的另一模式——最优评分问题中，李国权等^[16^]在2021年提出了加入正则项的稀疏最优评分问题，并用迭代算法进行求解。受此系列文章启发，我们提出以下基于正则项的稀疏Fisher线性判别模型。

2.3　加入正则项的模型

Fisher LDA寻找线性函数β^Tx，使得类间平方和与类内平方和的比率最大化，形式上，考虑一个简单的多元高斯模型，即第k类的分布为，μ_k∈是均值向量，是p×p的类内方差矩阵，假设有K个类别并设x_ij，j=1，…，n_i是第i类观测值的向量，i=1，…，k，令n=n₁+…+n_k，表示第i类的平均值。则Fisher判别问题可表示为:

s.t.∑_wβ_l=0.(∀l≤k)

μ_k的估计为表示第k类的指标集。π_k是第k类的先验概率，

标准的组内方差协差阵估计量为:

其中，是第k类的样本均值向量。

标准的组间方差估计量为:

为解决矩阵奇异问题，一种简单方法是使用广义逆矩阵，例如Duintjer Tebbens^[17^]在2007年提到的Moore-Penrose伪逆矩阵。尽管它很简单，但这种方法可能性能不佳，因为同年，Guo等^[18^]已表明广义逆由于缺乏观测值而非常不稳定。Krzanowski等^[6^]在其文献中考虑修改原问题，转而寻找一个单位向量β，最大化。还有一种常用方法是在Fisher判别问题中使用类内协方差矩阵的正则化估计。例如:

β^T∑_bβ_k　　　　　　　　　　　　

Hastie、Buja 和 Tibshirani在文章中采用了这种方法，是正定的，因此，即使p≫n，问题中的判别向量也可以计算，此外，合适的Ω可以得出平滑的判别向量^[19^]。而Friedman等^[20^]考虑了对角阵估计。

其中，是的第j个对角元，在本文中，我们使用的是是对角线估计的情况，因为已经表明，当p>n时，对∑_w使用对角线估计可以导致良好的分类结果^[2^]。

为解决正交约束，下面我们将用到这样一个引理。

引理1:以下两个问题的解等价:

式中，=n^-1X^TY(Y^TY)^-1/2(Y^TY)^-1/2Y^TX，定义如下:=I，对于k>1，是(Y^TYY^TX， i<k张成的线性空间的补空间上的正交投影算子。

引理1的证明见参考文献[10]中的附录A.2，当求出，…，时，用替代原先的组间方差，重复之前的求解过程，直到得到所有的判别向量。

则原问题转变为:

求解上述问题相当于求解:

为得到稀疏的判别向量，对上式实施l₀惩罚

由于上述问题是非凸非光滑且NP-难，我们转为用l_q范数逼近，上式转化为:

其中，为了克服由‖β_k引起的非光滑性，引入常规参数ε，上式转为:

其中，‖β_k=(∈+[β_k)^q/²，[β_k]_j表示β_k的第j个元素，当ε足够小的时候，‖β_k是‖β_k的一个较好的近似。

(0<q≤1)(3.1)

3　算法及收敛性分析

3.1　算法

问题(3.1)的局部最小值点需满足以下梯度方程

令D_l=diag，则上式可以写作:

(4.1)

算法1:

设置一个初始点∈，令l=0

如果k>1，定义一个正交投影矩阵，投影到正交于(Y^TY)^-1/2Y^TX的空间上，∀i<k.令:

循环以下步骤:

(1)通过等式(4.1)利用计算.

(2)l=l+1.

直到‖β^(l⁾-β^(l+1⁾‖²收敛时停止循环。

3.2　收敛性分析

为证明其收敛性，需要用到以下定理:

定理1.对于∈>0，∀α，β并且0<q<1，有

(∈+α²-(∈+β²-≥0.(4.2)

定理2.令∈>0，且{β^(l⁾是由算法1产生的序列，则序列{L_q(∈，β^(l⁾下降且收敛，即L_q-L_q≥0。

证明:

由于上述梯度等式(4.1)可以写作:

则:

利用不等式(4.2)，可得:

因此，序列{L_q(∈，β^(l⁾是下降的，由于L_q(∈，β^(l⁾)对于任意β∈都是非负的，因此序列同样是收敛的。

定理3.令∈>0并且0<q<1则对任意初始点β⁰∈，由算法1产生的序列{β^(l⁾都收敛到问题(3.1)的局部最小值点。

证明:

由定理2，已知序列{L_q(∈，β^(l⁾)是下降的，且下界为0，因此可以假设存在M≥0，使得L_q(∈，β^(l⁾)=M则有:

‖‖≤‖β^(l⁾‖_q_，∈≤L_q(∈，β^(l⁾)≤M+1.

对于足够大的l，有‖‖是有界的，那么存在收敛子序列{和点∈使得=。此外，由(4.1)可知，{β^(l⁾的子序列{同样也是收敛的，即存在β∈，使得=.又由于L_q(∈，β^(l⁾)在上是连续的，所以有L_q(∈，)=L_q(∈，)，因此，由定理2可得

0=L_q(∈，)-L_q(∈，)≥(-)^T(D_l/2)(-)≥0.

即(-)^T(D_l/2)(-)=0，则=，证毕。

4　总结与展望

4.1　总结

本章首先针对传统线性判别分析在高维情形下类内协方差矩阵奇异以及缺乏解释性这两个问题，建立了一种求解第k个判别成分的模型，该模型在原模型的基础上利用类内方差的对角估计矩阵代替原始类内协方差矩阵，克服了矩阵奇异的问题，同时将其投影到正交投影空间上，去掉了其正交约束，最后加入了l_q范数正则项，获得稀疏解，增强其解释性，并提出了求解该模型的迭代算法。最后给出了该算法的收敛性证明。

4.2　展望

本文在研究具有l_q正则项的稀疏判别分析的问题上，虽然详细讨论了求解第k个判别变量的模型和算法，但是并没有应用于实际问题中，对于是否可以有效改善其解释性，以及对线性判别分析的分类效果是否有积极作用缺乏说服力。因此可以将其应用于具体问题，观察其分类效果以及降维后数据的解释性是否得到有效提高。

利益冲突: 作者声明无利益冲突。

^{^[①]} *通讯作者　Corresponding author:高彩霞，2954993678@qq.com
收稿日期:2023-05-29;　录用日期:2023-06-21;　发表日期:2023-09-28

参考文献(References)

[1] Taibi F, Akbarizadeh G, Farshidi E. Robust reservoir rock fracture recognition based on a new sparse feature learning and data training method[J]. Multidimensional Systems and Signal Processing, 2019, 30(4): 390-403.
[2] Sharifzadeh F, Akbarizadeh G, Kavian Y S. Ship Classification in SAR Images Using a New Hybrid CNN-MLP Classifier[J]. Journal of the Indian Society of Remote Sensing, 2019, 47(4): 551-562.
https://doi.org/10.1007/s12524-018-0891-y
[3] Zhang Z Y, Wang J, Zha H Y. Adaptive manifold learning[ J]. IEEE transactions on pattern analysis and machine intelligence, 2012, 34(2): 253-265.
https://doi.org/10.1109/TPAMI.2011.115
[4] Hand D J. Classifier Technology and the Illusion of Progress[J]. Statistical Science, 2006, 21(1): 1-15.
[5] Clemmensen L, Hastie T, Witten D, et al. Sparse discriminant analysis[J]. Techonometrics, 2011, 53(4): 406-413.
https://doi.org/10.1198/TECH.2011.08118
[6] Krzanowski W J, Jonathan P, McCarthy W V, et al. Discriminant Analysis with Singular Covariance Matrices: Methods and Applications to Spectroscopic Data[J]. Journal of the Royal Statistical Society. Series C(Applied Statistics), 1995, 44(1): 101-115.
[7] Guo Y, Hastie T, Tibshirani R. Regularized linear discriminant analysis and its application in microarrays[J]. Biostatistics(Oxford, England), 2007, 8(1): 86-100.
[8] Zou H, Hastie T, Tibshirani R. Sparse Principal Component Analysis[J]. Journal of Computational and Graphical Statistics, 2006, 15(2): 265-286.
[9] Qiao Z H, Zhou L, Huang J Z. Sparse Linear Discriminant Analysis with Applications to High Dimensional Low Sample Size Data[J]. IAENG International Journal of Applied Mathematics, 2009, 39(1): 48.
[10] Witten D M, Tibshirani R. Penalized classification using Fisher's linear discriminant[J]. Journal of the Royal Statistical Society. Series B, Statistical methodology, 2011, 73(5): 753-772.
https://doi.org/10.1111/j.1467-9868.2011.00783.x
[11] Shao J, Wang Y Z, Deng X W, et al. Sparse linear linear discriminant analysis by thersholding for high dimensional data[J]. The Annals of Statistics, 2011, 39(2): 1241-1265.
https://doi.org/10.2307/29783672
[12] Trevor H, Andreas B, Robert T. Penalized Discriminant Analysis[J]. The Annals of Statistics, 1995, 23(1): 73-102.
[13] Esedo 􀭺glu S, Osher S J. Decomposition of images by the anisotropic Rudin-Osher-Fatemi model[J]. Communications on Pure and Applied Mathematics, 2004, 57(12): 1609-1626.
https://doi.org/10.1002/cpa.20045
[14] Yin Q, Shu L. Sparse linear discriminant analysis via l0 constraint[J]. Journal of University of Science and Technology of China, 2022, 52(08): 21-27.
[15] Hoai A L T, Duy N P. DC programming and DCA for sparse optimal scoring problem[J]. Neurocomputing, 2016, 186(1): 170-181.
https://doi.org/10.1016/j.neucom.2015.12.068
[16] Li G Q, Duan X X, Wu Z Y, et al. Generalized elastic net optimal scoring problem for feature selection[J]. Neurocomputing, 2021, 447(447): 183-195.
https://doi.org/10.1016/J.NEUCOM.2021.03.018
[17] Duintjer T J, Schlesinger P. Improving implementation of linear discriminant analysis for the high dimension small sample size problem[J]. Computational Statistics and Data Analysis, 2007, 52(1): 423-437.
https://doi.org/10.1016/j.csda.2007.02.001
[18] Guo Y, Hastie T, Tibshirani R. Regularized linear discriminant analysis and its application in microarrays[J]. Biostatistics, 2007, 8(1): 86-100.
[19] 尹祺. 基于l0 惩罚下的主成分分析与线性判别分析[D]. 合肥: 中国科学技术大学, 2022.
https://doi.org/10.27517/d.cnki.gzkju.2022.000185
[20] Friedman J H. Regularized Discriminant Analysis[J]. Journal of the American Statistical Association, 1989, 84(405): 165-175.
[21] Mai Q, Zou H. A Note On the Connection and Equivalence of Three Sparse Linear Discriminant Analysis Methods[J]. Technometrics, 2013, 55(2): 243-246.

Sparse Linear Discriminant Analysis Based on lq Regularization

CHEN Jing, GAO Caixia^*

(School of Mathematical Science, Inner Mongolia University, Hohhot 010021, China)

Abstract: Linear discriminant analysis plays an important role in feature extraction, data dimensionality reduction, and classification. With the progress of science and technology, the data that need to be processed are becoming increasingly large. However, in high-dimensional situations, linear discriminant analysis faces two problems: the lack of interpretability of the projected data since they all involve all p features, which are linear combinations of all features, as well as the singularity problem of the within-class covariance matrix. There are three different arguments for linear discriminant analysis: multivariate Gaussian model, Fisher discrimination problem, and optimal scoring problem. To solve these two problems, this article establishes a model for solving the kth discriminant component, which first transforms the original model of Fisher discriminant problem in linear discriminant analysis by using a diagonal estimated matrix for the within-class variance in place of the original within-class covariance matrix, which overcomes the singularity problem of the matrix and projects it to an orthogonal projection space to remove its orthogonal constraints, and subsequently an lq norm regularization term is added to enhance its interpretability for the purpose of dimensionality reduction and classification. Finally, an iterative algorithm for solving the model and a convergence analysis are given, and it is proved that the sequence generated by the algorithm is descended and converges to a local minimum of the problem for any initial value.

Keywords: Linear discriminant analysis, sparse optimization, lq norm, projection

DOI: 10.48014/fcpm.20230529001

Citation: CHEN Jing, GAO Caixia. Sparse linear discriminant analysis based on lq regularization[J]. Frontiers of Chinese Pure Mathematics, 2023, 1(2): 31-38.