基于稀疏贝叶斯的Dirichlet问题求解方法-HTML全文-中国理论数学前沿-科学足迹出版社(SFP)

基于稀疏贝叶斯的Dirichlet问题求解方法

杨东华, 莫艳^*

(广东工业大学数学与统计学院, 广州510520)

摘要: 偏微分方程与许多实际问题有着密切的联系, 由于其通常不易获得解析解, 其数值解法是众多学者研究的热门课题。稀疏贝叶斯学习是近年来机器学习的研究热点。相关向量机 (Relevance Vector Machine, RVM) 是一种基于稀疏贝叶斯学习的学习机, 在解决逼近问题上表现出良好的性能。本文基于再生核理论和相关向量机, 提出了一种求解离散及非离散Dirichlet问题的新方法。基于再生核理论构造满足方程条件的再生核空间, 把方程求解问题转化为相应的目标优化问题, 然后在相关向量机框架中进行求解, 得到以再生核线性组合稀疏表示的近似解。相比于传统方法, 本文方法不需要画网格; 相较于一般的机器学习方法, 本文方法基于对超参数的处理具有出色的避免过拟合的能力, 能够计算出结果的后验概率分布以提供不确定性量化, 不需要交叉验证过程设置额外的正则化参数, 减少了模型的复杂度, 提高了模型的泛化能力、可解释性和效率。稀疏性分析说明了所提方法的稀疏性质和扩展到高维问题的可能性。与常用的有限差分法、神经网络方法以及支持向量机方法的对比实验结果表明, 所提方法具有较好的稀疏性、鲁棒性以及有效性。

关键词: Dirichlet问题, 稀疏贝叶斯, 相关向量机, 高斯再生核Hilbert空间, 稀疏解

DOI: 10.48014/fcpm.20240312002

引用格式: 杨东华, 莫艳. 基于稀疏贝叶斯的Dirichlet问题求解方法[J]. 中国理论数学前沿, 2024, 2(2): 5-15.

文章类型: 研究性论文

收稿日期: 2024-03-12

接收日期: 2024-04-07

出版日期: 2024-06-28

偏微分方程在生活中有着极为广泛的实际应用，是许多热门的基础研究课题之一。然而，在科学研究、生产和应用等社会活动中所遇见的微分方程大多十分复杂，不易求得其解析解。因此，用数值方法研究偏微分方程的近似解仍具有重要的意义。

传统的求解微分方程的方法如有限元(Finite Element Method，FEM)，有限差分法(Finite Difference Method，FDM)等通过节点网格加密并迭代求得数值解^[1^,2^]。然而，当涉及实际的偏微分方程和高维度问题时，维度的增加会导致网格节点数呈指数级增加，即所谓的维数灾难。网格数量以指数方式增加，这导致计算资源需求急剧增加，意味着更多的内存和计算时间以及数值不稳定。

与经典的有限元和有限差分法相比，人工神经网络(Artificial Neural Networks，ANN)方法依赖于其前馈神经网络的函数逼近能力，不需要画网格，可得到相对较精确且具有解析表达式的近似解，但需选取恰当的权重参数和损失函数^[3-5^]。这种形式采用前馈神经网络作为基本逼近元素，调整其参数(权重和偏差)以最小化适当的损失函数。依据选取不同的损失函数，ANN方法会有数据驱动和物理信息驱动的区别。数据驱动下，神经网络受到较强的约束，更容易收敛，但其应用场景有限。然而，在物理信息驱动下，如果少了标签数据的约束，深度学习的收敛将非常困难，大量的科学技术问题亟待解决^[6-8^]。

微分方程通常是某些物理规律的数学表示，在许多物理现象中，观测数据只能在有限个离散点上获得，因此研究离散微分方程具有重要的意义。然而，上述提到的求解微分方程的算法对于求解离散微分方程都将失效。

日本学者Saitoh等在文献[9，10]中利用Tikhonov正则化和再生核理论，给出了求解离散线性微分方程及其逆问题的方法。该方法可以应用于不同的离散线性微分方程，利用再生核Hilbert空间的性质可以得到解的解析表达式。进一步，在文献[11]中Saitoh等利用Tikhonov正则化、Dirichlet原理以及再生核理论对Dirichlet问题进行求解，得到Dirichlet问题的一个近似解，该方法对于离散Dirichlet问题同样适用。但该方法需要N次迭代来计算再生核(N是给定的离散点的个数)，比较耗时且计算精度还需提升。在此基础上，文献[12]和[13]提出了一种结合Tikhonov正则化、支持向量机(Support Vector Machine，SVM)算法以及再生核理论的数值求解Dirichlet问题和离散线性微分方程的方法。利用所提出的方法，在求解微分方程问题中，获得以特定函数的线性组合表示的稀疏解来逼近期望的精确解。所提方法无论是对非离散微分方程问题还是离散微分方程问题都适用。但是该方法基于SVM算法给出，受限于SVM一些自身固有的缺陷:比如SVM的核函数必须满足Mercer条件，限制了其应用范围;SVM所得结果有一定的稀疏性，但支持向量的数目通常随训练集的大小呈线性增长，稀疏性还可以进一步提高;通常无法计算其输出的后验概率分布，导致无法判断计算结果的可靠性，为此往往还需要增加复杂的后续处理。

稀疏贝叶斯学习(Sparse Bayesian Learning，SBL)是在贝叶斯理论的基础上发展起来的，是一类非常重要的贝叶斯统计优化算法^[14^,15^]。SBL算法根据样本信息，将待估计的未知参数向量视为符合一定先验分布的随机向量，利用贝叶斯定理计算后验概率分布，从而推断未知参数。相关向量机(Relevance Vector Machine，RVM)^[¹⁶^,17^]是建立在稀疏贝叶斯学习基础上的学习机器，由Michael E. Tipping于2001年提出。RVM既保持了支持向量机的优点，又克服了支持向量机的一些缺陷^[18^]。RVM也使用核函数进行映射，然而，放宽了核函数选择的限制。RVM基于稀疏贝叶斯框架构建学习机，不需要交叉验证过程来设置额外的正则化参数，能够得到概率形式的输出，并且其参数线性模型通常比SVM更为稀疏。

为克服以上介绍方法存在的缺点，以期望获得更好的求解稳定性、精度以及稀疏性质，我们结合稀疏贝叶斯理论和再生核理论，来数值求解Dirichlet问题，我们的算法将会用到一个新构造的再生核函数(核函数)，相应的算法称为SBL-算法。所提出算法对非离散和离散Dirichlet问题都适用。该方法在有高斯噪声干扰及无高斯噪声干扰两种情况下都表现出良好的性能，所获得的解是再生核函数(核函数)的线性组合形式的稀疏表示。通过与有限差分法、SVM算法的比较，可以看到用SBL-算法得到的解比较稀疏的同时，具有良好的泛化性能，即获得提高精度和稀疏性的双重好处。

1　Dirichlet问题

本文将提出一种构造Dirichlet问题近似解的新方法。考虑微分方程为:

(1.1)

其中，D为一有界区域，其边界用∂D表示，函数h属于某个再生核空间。给定g，求出函数h.

如前面所说，很多物理现象中，我们只能在有限个点上得到观测数据，对于离散微分方程的解的研究十分重要。本文所提方法同样适用于如下的离散Dirichlet 问题:

(1.1)^*

给定，求函数h.

由于Gaussian核具有良好的性质，本文将考虑在Gaussian-RKHS(Gaussian-Reproducing Kernel Hilbert Space，高斯再生核Hilbert空间)中求解微分方程。

Gaussian-RKHS定义为^[19^]:

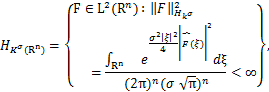
其中，是F的傅里叶变换:

该空间的再生核为:

K^σ(x，y)=，

其中x，y∈Rⁿ，σ>0.

根据Dirichlet原理，求解方程(1.1)可化为求解一个极值函数的问题。在满足边界条件F=g(on ∂D)的情况下，如果函数F是使相应Dirichlet积分极小化的极值函数，那么F就是方程(1.1)的解。当满足条件的极值数F存在时，我们寻求如何更好表示该函数。

基于此，结合Tikhonov正则化与再生核理论，求解问题(1.1)或者(1.1)^*的步骤分为两步:首先，对于给定的λ>0，给定边界∂D上任意给定N个点(其中x∈Rⁿ)和这些点对应的函数值(亦即是g(x_j)=t_j，j=1，…，N)，以及相应地任意给定的常数C_j>0，求解:

(1.2)

对于每一个给定的λ>0，求解(1.2)得到极值函数F=(x).然后，通过在相应的极值函数(x)中取极限λ→0，则最后可得到原始问题(1.1)的解析解h=F.

注1.1:问题(1.2)选择了来衡量模型预测值与真实值之间的差异，具体情况根据模型的需要，也可以选择其他的损失函数。

由下面的定理1.1可以进一步将问题(1.2)转化。

定理1.1^[⁹^]:设H_k是集合E上的Hilbert空间，它有再生核K(p，q)。设L是从H_k到H的有界线性算子(在这里，H也是一个Hilbert空间)。对于λ>0，令由H_k导出的空间的内积为

=+，

那么也是集合E上的Hilbert空间，其具有再生核K_λ(p，q)，并且满足下面式子:

K(·，q)=(λI+L^*L)K_λ(·，q)，

其中，L^*是L的共轭算子。

根据定理1.1，由再生核Hilbert空间可以导出再生核Hilbert空间，其范数和再生核分别为:

=，

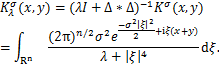
基于上述结果，问题(1.2)可等价表述为求解下述问题:

(1.3)

本文将从贝叶斯理论的角度，把问题(1.3)放在稀疏贝叶斯学习框架中考虑，将稀疏贝叶斯理论与再生核理论结合，提出SBL-数值求解方法，求得以特定函数线性组合表示的解，且该解具有较为良好的稳定性和稀疏性质。然后，通过取极限λ→0，最后就可求得原始问题(1.1)或(1.1)^*的解。

2　基于稀疏贝叶斯的求解方法

对于给定的λ>0，在边界∂D上任意给定N个点(其中x∈Rⁿ)和这些点对应的函数值(亦即是g(x_j)=t_j，j=1，…，N)，以及相应地任意给定的常数C_j>0，我们的目标是求解下述问题:

(2.1)

假设问题(2.1)的数值解具有以下形式:

(2.2)

其中，W=是上式(2.2)中待求的权重参数向量。

那么，接下来的问题便是，根据给定的数据集(作为已知的先验信息)，在稀疏贝叶斯框架下进行参数估计，求出W，最后求出问题(2.1)的解。

由于数据噪声和模型误差的真实存在，数值解与精确解之间存在差异。对于给定的数据集，有:

T=F(X;W)+E，(2.3)

其中，T，F(X;W)=(F(x₁;W)，F(x₂;W)，…，F(x_N;W))^T，E，单个独立样本残差为:􀆠_j=t_j-F(x_j;W)=g(x_j)-F(x_j;W)，j=1，…，N.

将式(2.2)和(2.3)改写成向量形式，如下:

F(X;W)=ΦW，

T=ΦW+E，

其中，Φ=，ϕ(x_j)=，亦即有:

Φ=.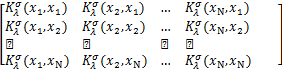

假设残差􀆠_j=t_j-F(x_j;W)服从零均值方差为σ²的高斯分布，即

p(􀆠_j)=N(􀆠_j|0，σ²)=exp，

那么有p(t_j)=N(t_j|).

从而，基于数据样本的独立性假设，整个给定数据集的似然函数为:

(2.4)

在W上引入一个零均值高斯先验分布:

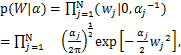
α_j为未知超参数，控制W的稀疏程度，超参数向量α=.

由上面已经得到的数据集似然函数和权重参数先验分布，通过对权重参数进行积分，可得到超参数的边际似然函数(Marginal Likelihood)，为:

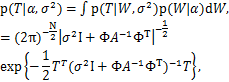
其中，I是单位矩阵，A=diag(α₁，…，α_N).

通过计算归一化积分p(T|α，σ²)，把整个W在参数空间中积分掉，也就是说把每一个参数w_j的取值都考虑进去，这给予了模型能自动平衡拟合精度和复杂度的能力。

接下来是在稀疏贝叶斯框架中估计超参数。注意到，与超参数α一样，σ²同样可以被认为是超参数，可以通过已知数据集对模型进行参数估计得到。基于RVM理论，p(T|α，σ²)中的超参数α和σ²，可以通过第二类极大似然(type-II maximum likelihood)迭代估计得到^[15^]。记它们的估计值分别为α_MP和.

当超参数α和σ²的估计值求出来后，权重参数向量W的最大后验估计(Maximum a Posteriori，MAP)可以由下面的权重后验分布的均值u得出。

权重参数W的后验分布为:

p(W|T，α，σ²)=

=(2π

exp，

=N(W|u，Σ)，

其中，后验协方差Σ=，后验均值u=σ^-2ΣΦ^TT，A=diag(α₁，…，α_N).

那么，通过把所得到的超参数估计值α_MP和代入上面的权重参数W后验分布，可相应地计算得到权重后验后验协方差估计值Σ_MP和后验均值估计值u_MP，进而可以得出权重W的估计值，即有W==u_MP.

一般情况下，我们通常采用一个具体函数表达式(或对应法则)来描述变量之间的关系。那么，得到变量之间的关系描述，即解决了一般意义下的函数推断问题。对于一个新的任意点x(自变量)，记t(因变量)是其对应的精确函数值，F(x;W)是数值方法的参数线性模型，􀆠是残差(衡量数据噪声和模型误差)，它们的关系描述为:

t=F(x;W)+􀆠.

而从贝叶斯的角度，变量x与t之间的关系，可以通过一个条件概率p(t|x)来描述^[17^]。回到我们的问题，把已知的给定数据集作为先验信息，在通过稀疏贝叶斯学习理论求得模型的参数估计值之后，我们就可以基于所得模型，对一个新的任意点x，“预测”出其对应的函数值t的分布，亦即是得到变量x与t之间的概率角度的关系描述。

在这里，与前面所作出的说明一样，为了清楚简便地说明内容，在随后的表达式当中省略了N个给定点和自变量x的隐含条件。根据已求得的超参数估计值，所求的条件概率可以表述如下:

=N(t|ϕ(x)，

+ϕ(x)^TΣ_MPϕ(x))，

其中，ϕ(x)=[(x₁，x)，(x₂，x)，…，(x_N，x)]^T.

那么，我们就得到了所求的稀疏贝叶斯参数线性模型(亦即问题(2.1)的数值解)，为:

=ϕ(x)，

其中，是通过计算得到的权重后验均值估计值向量的转置，亦即是(w₁，…，w_N)=.

需要说明的是，我们在得到问题的解的表达式的同时，更是得到概率式的“预测”分布函数，有助于判断计算结果的可靠性。

基于RVM理论，在估计超参数α和σ²的迭代更新过程中，绝大部分的超参数α_i会趋于无穷大，那么基于在权重参数上定义的由超参数控制的概率分布p(W|α)，这些α_i所对应的w_i将被设置为0，这样便导致模型变得稀疏。而那些与不为零的w_j对应的少数样本点x_j就被称为相关向量(relevance vector)^[¹⁴^]。

在此框架下，问题(2.1)的解可以改写为:

(2.5)

其中，J是相关向量的索引集，|J|≤N.

最后，在式(2.5)中让λ趋于0，得到问题(1.1)或问题(1.1)*的解h=lim_λ_→0F(x;W).

3　稀疏性分析

根据ARD(Automatic Relevance Determination，自动相关确定)理论^[15^]，模型的稀疏意味着将模型中大部分的权重参数w_i通过“学习”过程自动相关地设置为0。在机器学习中，模型稀疏性的高低程度会影响特征学习效率，亦即影响模型解决问题的能力，其重要性自然不言而喻。因此，对稀疏性的分析研究也受到了越来越多学者的关注。基于文献[17]、[20]和[21]，我们将对本文所提出的SBL-方法的稀疏性质进行分析。

所提模型的主要“学习”过程可以理解为:根据给定的已知数据集等先验信息，通过第二类极大似然估计过程，亦即是最大化超参数的边际似然函数，求得超参数的估计值。为了深入分析所提方法(模型)的稀疏性质，我们需要对第二类极大似然估计过程进行分析，从整体模型中分离出单个独立的超参数α_i和其对应的权重参数w_i，看看导致稀疏的过程是如何发生的。

最大化超参数α的边际似然函数，实际上等价于最大化该边际似然函数的对数，记为L(α)，

L(α)=lnp(T|α，σ²)

=ln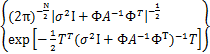

=-[Nln(2π)+ln+T^TC^-1T]，

其中，记矩阵C=σ²I+ΦA^-1Φ^T，I是单位矩阵，A=diag(α₁，…，α_N).

为分离出单个独立的超参数α_i，了解对单个独立的超参数α_i的极大似然估计过程并进行稀疏性分析，我们需要对矩阵C进行适当变化。

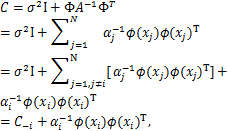
其中，ϕ(x_j)=[(x₁，x_j)，(x₂，x_j)，…，(x_N，x_j)]^T，Φ=[ϕ(x₁)，ϕ(x₂)，…，ϕ(x_N)]^T，记矩阵表示从矩阵C中去掉超参数α_i和核函数向量ϕ(x_i).

基于矩阵运算法则，矩阵C和C_-i的关系有以下式子:

=，

C^-1=-.

那么，超参数边际似然函数的对数L(α)可相应地整理为:

L(α)=- 说明: source:si_idp768466912;FounderCES Nln(2π)+ln+T^TT-lnα_i+

ln(α_i+ϕ(x_i))-

说明: source:si_idp776832688;FounderCES

=-[Nln(2π)+ln+T^TT]+

说明: source:si_idp776936624;FounderCES lnα_i-ln(α_i+ϕ(x_i))+

说明: source:si_idp815623344;FounderCES

=L(α_-i)+，

其中，记L(α_-i)=-[N ln(2π)+ln+T^TT]表示去掉超参数α_i后的似然函数对数，记数值s_i=ϕ(x_i)，q_i=T.

那么，L(α)关于α_i的偏导数为:

==.

注:在极大似然估计过程，一般的步骤就是:首先求出待估参数的似然函数;其次，为了便于计算，对似然函数进行对数化;再次，根据对数式子关于待估参数求导数;最后，令导数为零并解该似然方程。

令=0，可求解得单个独立的超参数α_i的估计值为:

α_i=

注意，作为一个逆方差(inverse variance)，超参数α_i一定是正的，即α_i>0.

在实际的关于α进行最大化超参数边际似然函数(即第二类极大似然估计)的迭代计算过程中，大部分的超参数α_i趋于无穷大。一方面，由于在模型中预先对每个独立的权重参数w_i设置一个由对应超参数α_i控制的零均值高斯先验分布，即

p(w_i|α_i)=N(w_i|0，)，

那么当大部分的α_i趋于无穷大时，必然会影响大部分对应w_i被控制分布在均值0附近。另一方面，由模型的权重参数后验分布p(W|T，α，σ²)可得，与这些α_i对应的w_i的后验统计量估计值为:

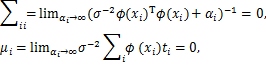
其中，是w_i的后验方差估计值(也就是权重后验协方差矩阵Σ中的第i个对角元素)，μ_i是w_i的后验均值估计值(亦即是权重后验均值向量u中的第i个元素)，表示权重后验协方差矩阵Σ中的第i行，ϕ(x_i)=[(x₁，x_i)，(x₂，x_i)，…，(x_N，x_i)]^T.那么，由上面w_i的后验统计量估计值可推断，p(w_i)=N(w_i|0，0)，亦即相当于w_i=0.

综上所述，在本文所提的SBL-方法中，对于超参数α的第二类极大似然估计，会在实际中使得大部分的α_i趋于无穷大，从而使得相对应的模型权重参数w_i被设置为0.那么，模型中与w_i对应的核函数(x_i，x)会被“修剪”，相应的这些样本点x_i被认为与模型的“学习”不相关，从而只有较少部分x_j(j≠i)被留下来构建模型，这就导致了模型的稀疏。

4　数值实验

在本节中，为验证所提算法的有效性，下面将以两个例子来说明。为方便与人工神经网络方法(ANN)及五点差分方法进行比较，以下例子中给出了边界函数g.如果只知道边界函数在某些点上的值，则ANN与五点差分法就不适用了。

为了便于评价和比较，我们采用两种常用的计量方法对结果的表现进行评价。一个是均方误差(Mean Squared Error，MSE)，

其中，设h为原始函数，f为近似函数。另一个是平方相关系数(Squared Correlation Coefficient，SCC):

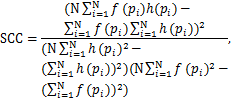
其中，p_i表示样本点(x_i，y_i)∈∂D，i=1，…，N。

实验1:我们将所提出的SBL-算法与人工神经网络(ANN)方法进行对比。考虑Dirichlet边值问题，区域为D=[0，1]×[0，1]。将[0，1]分为20等分，以等距在x轴和y轴上取边界点，得到400个点的网格。求解如下边值问题:

，

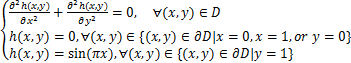问题的解析解为:

h(x，y)=sin(πx)(e^πy-e^-πy).

图1、2、3分别为方程解析解、ANN近似解和SBL-近似解的图示，可以看到两种机器学习方法都有不错的逼近效果。进一步，表1展示了两种方法求解该问题的MSE和SCC，结果表明SBL-求解方法在泛化性能上优于一般的人工神经网络(ANN)方法。

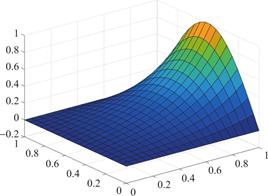
图1　解析解

Fig.1　The analytical solution

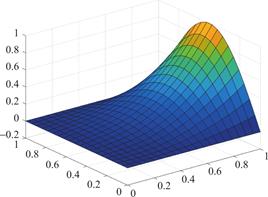
图2　ANN近似解

Fig.2　The approximated solution by ANN

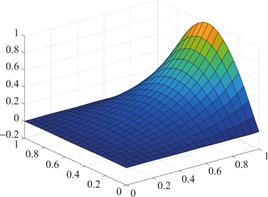
图3　SBL-近似解

Fig.3　The approximated graph by SBL-

表1　实验1数值结果

Table 1　The numerical results in experiment 1

	ANN	SBL-
MSE	4.2769e-04	2.2196e-06
SCC	0.9957	0.9998

实验2:我们将所提出的SBL-算法与五点差分法、SVM-Tik-算法^[12^]进行比较，为方便与五点差分法进行比较，以下例子中给出了边界函数g。

考虑在边界∂D上有g(x，y)=xy，(x，y)∈∂D，其中，区域D为[-0.25，0.25]×[-0.25，0.25]-[-0.25，0]×[-0.25，0](L型区域)。实验考虑的变量情况包括:数据在有高斯噪声干扰(其中分别设置SNR=30和SNR=20)和无高斯噪声干扰的情况;以及，在边界上分别取点N=80(即步长为0.025)和N=160(即步长为0.0125)的情况。即对于作为实验输入的数据集，给予其不同程度的高斯噪声干扰和不同数量的采样点。另外，定义稀疏度为:

Sparseness=×100%，

其作为SNR和样本数量的函数，评估解的稀疏程度随着SNR的降低和样本的增加的变化情况。

图4展示了五点差分法、SVM-Tik-算法和SBL-算法在存在高斯噪声(SNR=30)情况下的性能。可以看到五点差分法对噪声的鲁棒性不如SVM-Tik-算法和SBL-算法。表2和表3分别显示了稀疏度作为SNR(即SNR作为自变量，固定N=160)和样本数量N(即样本数量N为自变量，固定SNR=20)的函数，表现不同算法得到的解的稀疏性。可以看到，相比于SVM-Tik-，SBL-得到的解的稀疏度更高，即SBL-具有更好的稀疏性质。表4和表5显示了不同噪声情况下三种算法的性能表现。可以看到，在无噪声的情况下，五点差分法的效果优于SVM-Tik-和SBL-，但有噪声的情况下，五点差分法受噪声的影响较大，效果不如另外两种算法。SVM-Tik-和SBL-对噪声较为鲁棒，二者相比，在不同噪声情况下，本文所提出的算法SBL-的效果均优于SVM-Tik-.SBL-算法得到的解在比较稀疏的同时，具有良好的效果。总的来说，本文所提出的SBL-算法是一种有效的方法。

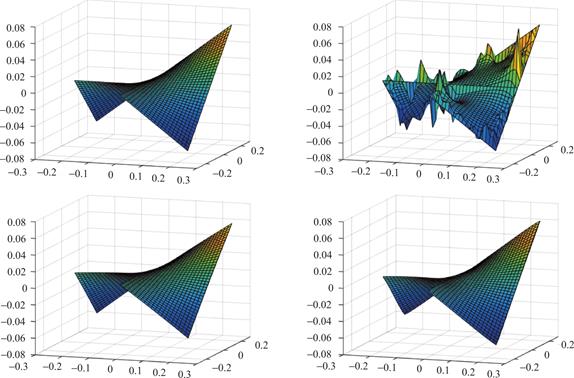
图4　左上角为h(x，y)=xy的精确图。在边界∂D上给定160个高斯噪声干扰样本点(SNR=30)。右上角为采用五点差分法的近似图。左下角为采用SVM-Tik-算法^[⁸^]的近似图。右下角为所提出的SBL-算法的近似图

Fig.4　The exact graph of h(x，y)=xy(top left).160 Gaussian noise(SNR=30)corrupted points are given on the boundary.The upper right corner shows the approximate plot using the five-point difference method.The bottom left corner shows the approximate plot using the SVM-Tik- algorithm ^[⁸^].The bottom right corner shows the approximate graph of the proposed SBL- algorithm

表2　不同信噪比下的稀疏度

Table 2　Sparseness with SNR

Method	Noise
Method	No noise	30dB	20dB
SVM-Tik-	6.25%	21.88%	33.38%
SBL-	13.13%	10.00%	4.37%

表3　不同样本数量下的稀疏度

Table 3　Sparseness with number of samples

Method	Number of samples
Method	80	160
SVM-Tik-	20.62%	25.00%
SBL-	9.37%	10.00%

表4　不同信噪比下的均方误差

Table 4　MSE with SNR(Gaussian noise)

Method	Noise
Method	No noise	30dB	20dB
SVM-Tik-	3.4562e-005	3.3182e-005	8.5398e-004
SBL-	1.5608e-008	7.1235e-008	3.2378e-006
五点差分法	7.0266e-034	3.6362e-005	4.0248e-004

表5　不同信噪比下的平方相关系数

Table 5　SCC with SNR(Gaussian noise)

Method	Noise
Method	No noise	30dB	20dB
SVM-Tik-	0.9992	0.9945	0.9934
SBL-	0.9998	0.9968	0.9927
五点差分法	1	0.9578	0.5758

5　结论

本文提出了一种基于稀疏贝叶斯、再生核理论和Tikhonov正则化的求解Dirichlet问题的方法。该方法同样适用于一般的微分方程，且所提的算法不仅适用于非离散微分方程问题，对于离散的微分方程问题同样适用。通过将Dirichlet问题转化为相应的目标优化问题并构建相应的模型，结合再生核理论，在稀疏贝叶斯框架下对该问题进行求解，得到以再生核函数线性组合稀疏表示的近似解，所得解对噪声具有鲁棒性。所提出的算法不需交叉验证过程来设置额外的正则化参数，且其得到的解通常更为稀疏。实验结果证明了所提方法的有效性。

利益冲突: 作者声明无利益冲突。

^{^[①]} *通讯作者　Corresponding author:莫艳，marvel-2008@163.com
收稿日期:2024-03-12;　录用日期:2024-04-07;　发表日期:2024-06-28
基金项目:广州市科技计划(202102020704)

参考文献(References)

[1] SMITH G D. Numerical Solution of Partial Differential Equations: Finite Difference Methods[M]. Clarendon Press, Oxford, 1978.
[2] 李荣华. 偏微分方程数值解[M]. 北京: 高等教育出版社, 2007.
[3] LAGARIS I E, LIKAS A C. Artificial neural networks for solving ordinary and partial differential equations[J]. IEEE Transactions on Neural Networks, 1998, 9(5): 987-1000.
[4] KEVIN S. MCFAll, JAMES R. MAHAN. Artificial Neural Network Method for Solution of Boundary Value Problems with Exact Satisfaction of Arbitrary Boundary Conditions[J]. IEEE Transactions on Neural Networks, 2009, 20(8): 1221-1233.
https://doi.org/10.1109/TNN.2009.2020735
[5] JUSTIN A SIRIGNANO, KONSTANTINOS SPILIOPOULOS. A deep learning algorithm for solving partial differential equations[J]. Computational Physics, 2018, 375: 1339-1364.
https://doi.org/10.1016/j.jcp.2018.08.029
[6] MAZIAR RAISSI, PARIS PERDIKARIS, GEORGE EM KARNIADAKIS. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations[J]. Computational Physics, 2019, 378: 686-707.
https://doi.org/10.1016/j.jcp.2018.10.045
[7] MAZIAR RAISSI, ALIREZA YAZDANI, GEORGE EM KARNIADAKIS. Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations[J]. Science, 2020, 367: 1026-1030.
https://doi.org/10.1126/science.aaw4741
[8] JEREMY YU, LU LU, XUHUI MENG, et al. Gradientenhanced physics-informed neural networks for forward and inverse PDE problems[J]. Computer Methods in Applied Mechanics and Engineering, 2022, 393: 114823.
https://doi.org/10.1016/j.cma.2022.114823
[9] SAITOH S. Integral transforms, reproducing Kernels and their applications[M]. in: Chapman & Hall/CRC Research Notes in Mathematics Series 369. CRC Press, 1997.
https://doi.org/10.1201/9781003062301
[10] SAITOH S. Approximate real inversion formulas of the gaussian convolution[J]. Applicable Analysis, 2004, 83(7): 727-733.
https://doi.org/10.1080/00036810410001657198
[11] MATSUURA T, SAITOH S. Dirichlet principle using computers[J]. Applicable Analysis, 2005, 84(10): 989-1003.
https://doi.org/10.1080/00036810412331297208
[12] MO Y, QIAN T. Support vector machine adapted Tikhonov regularization method to solve Dirichlet problem[J]. Applied Mathematics & Computation, 2014, 245: 509-519.
https://doi.org/10.1016/j.amc.2014.07.089
[13] 王丹荣, 莫艳. 基于支持向量机的离散线性微分方程求解方法[J]. 广东工业大学学报, 2020, 37(02): 87-93.
https://doi.org/10.12052/gdutxb.190050
[14] SORIA O E, GOMEZ S J, MARTIN J D. BELM: Bayesian Extreme Learning Machine[J]. IEEE Transactions on Neural Networks, 2011, 22(3): 505-509.
https://doi.org/10.1109/TNN.2010.2103956
[15] TIPPING M E. Bayesian Inference: An Introduction to Principles and Practice in Machine Learning[C]. Advanced Lectures on Machine Learning, Ml Summer Schools, Canberra, Australia, February, Tübingen, Germany, August, Revised Lectures. Springer Berlin Heidelberg, 2004.
https://doi.org/10.1007/978-3-540-28650-9_3
[16] TIPPING M E. The Relevance Vector Machine[J]. In Proceedings of the 12th International Conference on Neural Information Processing Systems(NIPS'99), 1999, MIT Press, Cambridge, MA, USA, 652-658.
https://doi.org/10.5555/3009657.3009750
[17] TIPPING M E. Sparse Bayesian Learning and the Relevance Vector Machine[J]. Journal of Machine Learning Research, 2001, 1(3): 211-244.
https://doi.org/10.1162/15324430152748236
[18] XU X M, MAO Y F, XIONG J N, et al. Classification Performance Comparison between RVM and SVM[C]. 2007 International Workshop on Anti-Counterfeiting, Security and Identification(ASID), 2007: 208-211.
https://doi.org/10.1109/IWASID.2007.373728
[19] HA QUANG MINH. Some properties of gaussian reproducing kernel Hilbert spaces and their implications for function approximation and learning theory[J]. Constructive Approximation, 2010, 32(2): 307-338.
https://doi.org/10.1007/s00365-009-9080-0
[20] FAUL C ANITA, TIPPING E MICHAEL. Analysis of Sparse Bayesian Learning[J]. Neural Information Processing Systems, 2002: 383-390.
https://doi.org/10.5555/2980539.2980590
[21] LUO J, VONG C M, WONG P K. Sparse Bayesian Extreme Learning Machine for Multi-classification[J]. IEEE Transactions on Neural Networks & Learning Systems, 2017, 25(4): 836-843.
https://doi.org/10.1109/TNNLS.2013.2281839

Sparse Bayesian Based Method to Solve Dirichlet Problem

YANG Donghua, MO Yan^*

(School of Mathematics and Statistics, Guangdong University of Technology, Guangzhou 510520, China)

Abstract: Partial differential equations are closely related to many practical problems. Since they are usually difficult to obtain analytical solutions of partial differential equations, their numerical solution is a hot topic for many scholars. Sparse Bayesian learning is a hot research spot of machine learning in recent years. Relevance Vector Machine (RVM) is a learning machine based on sparse Bayesian learning, which shows good performance in solving approximation problems. In this paper, based on the reproducing kernel theory and relevance vector machine, a new method for solving discrete and non-discrete dirichlet problems is proposed. Based on the reproducing kernel theory, the reproducing kernel space satisfying the equation conditions is constructed, and the equation solving problem is transformed into the corresponding objective optimization problem. Then, the problem is solved in the framework of correlation vector machine, and the approximate solution is obtained by sparse representation of linear combination of reproducing kernels. Compared with the traditional method, this method does not need to draw the grid. Compared with the general machine learning method, this method in this paper has excellent ability to avoid over-fitting based on the processing of hyperparameters. It can calculate the posterior probability distribution of the results to provide uncertainty quantification. It does not need to set additional regularization parameters in the cross-validation process, which reduces the complexity of the model and improves the model’s generalization ability, interpretability and efficiency. Sparsity analysis shows the sparse nature of the proposed method and the possibility of extending it to high-dimensional problems. Comparison experiments with the commonly used finite difference method, neural network method and support vector machine method show that the proposed method has better sparsity, robustness and effectiveness.

Keywords: Dirichlet problem, sparse Bayesian, Relevance Vector Machine, Gaussian-RKHS, sparse solution

DOI: 10.48014/fcpm.20240312002

Citation: YANG Donghua, MO Yan. Sparse Bayesian based method to solve Dirichlet problem[J]. Frontiers of Chinese Pure Mathematics, 2024, 2(2): 5-15.