具有l1正则项的稀疏支持向量机的最优性条件及算法-HTML全文-中国理论数学前沿-科学足迹出版社(SFP)

具有l1正则项的稀疏支持向量机的最优性条件及算法

杨晓辉, 高彩霞^*

(内蒙古大学数学科学学院, 呼和浩特 010021)

摘要: 支持向量机 (SVM) 作为机器学习的主要方法之一, 是用于解决分类和回归任务的强大学习工具, 在图像分类、模式识别和疾病诊断领域都备受瞩目。在支持向量机模型中, L0/1损失函数是理想的损失函数, 已有的损失函数大多是其代理函数。稀疏优化是研究带有稀疏结构的最优化问题, 根据l1范数良好的稀疏性, 可以通过特征选择去除冗余特征, 本文在L0/1软间隔损失的模型基础上, 提出一个基于L0/1损失的l1范数稀疏支持向量机 (简称L0/1-SSVM) , 证明了模型解的存在性, 给出模型的KKT点和P-稳定点, 并证明全局最优解与KKT点的关系。利用l1范数的近端算子设计ADMM算法迭代框架, 并对算法进行收敛性分析, 证明其收敛于P-稳定点。

关键词: l1 范数, L0/1 损失, 稀疏支持向量机, 最优性条件, ADMM 算法

DOI: 10.48014/fcpm.20240411001

引用格式: 杨晓辉, 高彩霞. 具有l1 正则项的稀疏支持向量机的最优性条件及算法[J]. 中国理论数学前沿, 2024, 2(3): 16-24.

文章类型: 研究性论文

收稿日期: 2024-04-11

接收日期: 2024-05-22

出版日期: 2024-09-28

0　引言

稀疏优化问题的研究兴起于二十世纪九十年代，在本世纪得到了蓬勃的发展，已经广泛应用于机器学习^[1^]，信号处理与通信^[2^]，模式识别^[3^]，统计学中的回归问题^[4^]，经济学中的投资组合问题^[5^]以及主成分分析^[6^]等等。在机器学习领域中稀疏优化是重要的技术手段之一，其目的是可以在训练模型的过程中减少特征的数量，以此提高模型的泛化能力和可解释性，而支持向量机^[7^](Support vector machine，SVM)作为机器学习领域中的一种重要方法，对其进行稀疏优化则受到了广泛关注。

支持向量机是建立在统计学习理论的VC维理论和结构风险最小化原理^[8^]基础上的一种机器学习方法，在逻辑回归和神经网络相比，支持向量机在学习复杂的非线性方程时提供了一种更为清晰强大的方式，多用于解决数据挖掘和模式识别领域中数据分类问题，并且它在解决小样本、非线性和高维模式识别问题中表现出许多特有的优势。在实际生活中，支持向量机也广泛应用于各个领域。在图像识别^[9^]中，SVM可以实现人脸识别、物体检测等任务;在生物信息学中，SVM可以用于基因表达数据的分类和预测等任务;在金融市场中，SVM可以辅助分析股票走势和风险评估等任务。

正则项和损失函数是研究软间隔SVM的核心内容，不仅决定模型对训练数据的敏感性，还影响着模型的稀疏性。Cortes和Vapnik在文献[7]中指出，理想的损失函数是L_0/1损失函数，但L_0/1损失是非凸非连续的有界函数，具有NP难的特点，因此许多学者致力于构造新的代理损失函数，在算法和理论上也取得了丰富的研究成果，如Bartlett和Wegkamp^[10^]提出的广义合页损失函数，Jumutc和Huang^[11^]提出的弹球损失函数，沈晓彤^[12^]等人提出的滑道损失函数等等。文献[13]设法建立了L_0/1-SVM的最优性理论，提出一种快速的交替方向乘子法，通过数值实验验证了该算法求解L_0/1-SVM模型更高效。

在支持向量机中，常用到的正则项有l₀，l₁，l_p(0<p<1)，l₂范数等，其中l₂范数可以改善模型的过拟合，为大多数模型所使用的，但是不具备稀疏性，l₀范数指向量非零元素个数，具有很好的稀疏性，但由于其非凸比较难求解，而l₁范数是l₀范数的最优凸近似^[14^]，可以实现特征的自动选择，通过学习过滤掉冗余特征，因此很多学者致力于研究l₁范数为正则项的稀疏模型。Tanveer和Sharma^[15^]等人提出了具有弹球损失的稀疏支持向量机(Pin-SSVM)，所提出的模型使用l₁范数，保证了模型的稀疏性、鲁棒性和不敏感性;Zheng^[16^]等人提出稀疏支持矩阵机，新的正则化项是l₁范数和核范数的线性组合，同时考虑稀疏性和低秩性，使用广义前向后向算法进行求解，实验结果也证明了该模型具有优异的性能。

因此受其启发，本文在L_0/1损失函数的基础上，使用l₁范数作为模型的正则项，建立一个新的稀疏支持向量机模型，同时建立其最优性理论，并提出相应的ADMM算法求解，证明该算法是收敛的。

1　预备知识

1.1　符号与定义

本文向量默认为列向量，表示n维向量空间，x∈是一个n维向量，其中x_i表示向量的第n行。

定义1^[17^]　设f:Rⁿ→R是下半连续函数，则f在给定的x∈R处关于参数α>0的临近点算子定义为

prox_f(x):=argf(v)+(v-x)².(1)

定义2^[18^]　对给定参数η>0，l₁范数的临近点算子为

Pro(x)=sign(x_i)max

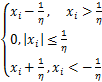=. (2)

定义3^[13^]　对给定参数γ>0，C>0，L_0/1范数的临近点算子为

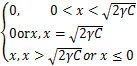Pro(x)=.(3)

定义4^[19^]　设f:Rⁿ→R在x∈R是局部Lipschitz的，那么f在x处的正则次微分是

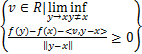f(x):=.(4)

定义5^[20^]　设Ω⊆是任意非空闭集，x^*∈Ω，则Ω在x^*∈Ω处的Bouligand切锥T_Ω(x^*)定义为

T_Ω(x^*):=.

(5)

则Ω在x^*∈Ω处的Clarke切锥(x^*)定义为

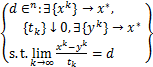(x^*):=.(6)

2　模型

2.1　模型发展

支持向量机的基本思想是寻找一个最优超平面将样本尽可能分开，并且使样本到超平面的距离尽可能的远。给定一个训练集{(x_i，y_i|i=1，…，m)}，其中x_i∈是输入向量，y_i∈{-1，1}是输出标签，y_i=+1和y_i=-1分别对应正类和负类。训练一个超平面<w，x>+b=w₁x₁+…+w_nx_n+b=0，使得对任意的输入向量x，都可以正确预测x的标签y，并且使输入向量距超平面的距离尽可能的远，将上述思想应用到二分类问题中可以得到如下模型:

‖w‖²+Cξ_i
s.t. yi₍<w，x>+b)≥1-ξi_，􁀂7)

其中C>0是惩罚参数，ξ_i是松弛变量，若样本可以完全分开，则不需要惩罚。或者是引入损失函数L(·)对分类错误的点进行惩罚，模型如下:

‖w‖²L+LC[1-y_i(<w，x>+b)]，(8)

其中前一项是正则项，衡量模型的复杂度，控制模型的稀疏;后一项损失函数控制模型的误差。理想的损失函数是L_0/1损失函数，2020年修乃华团队[13]提出L_0/1软间隔损失SVM，模型如下:

‖w‖²L+LC_0/1(1-y_i<w，x>+b)，(9)

其中L_0/1损失函数的表达式为:

L_0/1(t)=.(10)

该模型很好的捕捉到二分类的本质并且保证模型使用的支持向量更少，该模型的解决是支持向量机领域向前迈进了一大步，对于模型、理论和算法的更深入研究成为了有意义的方向。

2.1　L_0/1-SSVM模型

由文献[14]可知，l₁范数具有良好的稀疏性，为了减少冗余特征和提高模型的稀疏性，在L_0/1范数软间隔SVM模型的基础上，使用l₁范数作为正则项，提出如下新模型:

‖w‖₁L+LC_0/1，(11)

其中w∈是向量，b∈R是一个实数，‖·‖₁是向量中所有元素绝对值之和，C>0是惩罚参数，L_0/1是损失函数。

为了便于分析，设u:=e-Aw-by∈，其中e:=(1，1，…1)^⊥∈，A:=[y₁x₁ … y_mx_m]^⊥∈，y:=∈，则模型有如下转化:

(12)

其中u₊:=∈=max{u，0}，则L_0/1[1-y_i(w^⊥x_i+b)]=L_0/1(u)=，因此模型是本文提出的具有l₁正则项的稀疏支持向量机模型，简称L_0/1-SSVM，其中‖·‖₀是非凸非连续的，‖·‖₁是不可微的，因此上述问题是NP-难的，下文对其最优性条件进行分析。

2.2　最优性理论

通过引入变量s∈，模型有如下等价转化:

‖w‖₁+C
s.t.　　Aw+by=s，
e-s=u.􁀂( 3)

对应的拉格朗日函数为:

L(w，b，u，s，ρ₁，ρ₂)
=‖w‖₁+C+<ρ₁，s-Aw-by>+
　<ρ₂，u-e+s>，

其中ρ₁∈，ρ₂∈是拉格朗日乘子。

首先证明模型的全局最优解存在并且全局最优解解集是有界的。

定理1　若给定实数C∈[-K，K]，其中K是正数，则问题(12)的全局最优解存在且解集是有界的。

证明:由问题可知

f(w，b)≤f(e，b)<n+Cm<+¥.

对于f，由水平集

S:=.

由于(e;b)∈S，所以S≠∅，因此全局最优解存在。对于∀(w，b)∈S，有

‖w‖₁<f(w，b)≤n+Cm.

实数C∈[-K，K]，则S是有界的。由于L_0/1损失函数和范数均为下半连续函数，所以函数f也是下半连续函数，即问题的全局最优解存在且解集是有界的。

接下来给出模型的KKT点，并证明全局最优解与KKT点的关系。

定义6　对于模型(13)，给定C>0，称(w^*，b^*，u^*，s^*)是问题的KKT点，即如果存在∈，∈满足下式

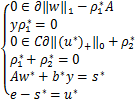.(14)

定理2　若(w^*，b^*，u^*，s^*)是问题(13)的全局最优解，如果存在D={(w，b，s)|s-Aw-by=0}，={d|d=‖w‖₁}，使得N_D(w)∩(w)={0}，则点(w^*，b^*，u^*，s^*)也是问题(13)的KKT点。

证明:若(w^*，b^*，u^*，s^*)是问题(13)的全局最优解，则也是可行解。即

要证明(w^*，b^*，u^*，s^*)也是KKT点，则需要证明

{‖w‖₁+C+(w，b，s)+(u，s)}

=(‖w‖₁，0，0，0)+(0，0，C，0)+

　(w，b，s)+(u，s). (15)

(1)对于∀(w，b，s)∈D₂，∀(u，s)∈D₂，根据定理显然有

(‖w‖₁，0，0，0)+(0，0，C，0)+

(w，b，s)+(u，s)⊆{‖w‖₁+

C+(w，b，s)+(u，s)}，

其中(w，b，s)，(u，s)各为D₁，D₂在(w，b，s)，(u，s)处的法锥。

(2)给定(r，r₁，r₂)∈{‖w‖₁+(w，b，s)}，根据定义4正则次微分，对∀(w，b，s)→(w^*，b^*，s^*)，有

o{‖(w，b，s)-(w^*，b^*，s^*)‖}

≤‖w‖₁+(w，b，s)--

　(w^*，b^*，s^*)-<r，(w-w^*)>-

　r₁(b-b^*)-<r₂，(s-s^*)>.

当(，，)→(w^*，b^*，s^*)且∈(w，b)∩Π_d，有=‖w‖₁，则

o{‖(w，b，s)-(w^*，b^*，s^*)‖}
≤-<r，(w-w^*)>-r₁(b-b^*).

则(r，r₁，r₂)∈，由于Π_d，D₁均为凸集，且N_D(w)∩(w)={0}，可得

(w，b，s)
=(w，b，s)+(w，b，s).

因此

(‖w‖₁+(w，b，s))
=‖w‖₁+(w，b，s).

同理给定(k₁，k₂)∈{C+(u，s)}，根据定义4正则次微分的定义，对于∀(u，s)→(u^*，s^*)，有

o{‖(u，s)-(u^*，s^*)‖}
≤C+(u，s)-C-
　(u^*，s^*)-<k₁，u-u^*>-<k₂，s-s^*>.

当(，)→(u^*，s^*)，且∈(u，s)，∈，其中I_x={i|u_i≠0}且={u∈|u_i≤0，i∉I_x}，则=，则

o{‖(u，s)-(u^*，s^*)‖}
≤-<k₁，u-u^*>-<k₂，s-s^*>.

则(u，s)∈，由于，D₂均为凸集，可得

(u，s)=(u，s)+(u，s).

因此

{C+(u，s)}
=C+(u，s).

即

{‖w‖₁+C+(w，b，s)+(u，s)}
⊆(‖w‖₁，0，0，0)+(0，0，C，0)+
(w，b，s)+(u，s).

综上所述，对于全局最优解(w^*，b^*，u^*，s^*)有式(15)成立，定理得证。

最后给出模型的P-稳定点。

通过引入变量z=w∈，将模型转化为

‖z‖₁+C
s.t.　　u+Aw+by=s，
z=w.􁀂( 6)

定义7　对于模型(16)，给定C>0，我们称(w^*，b^*，z^*，u^*)是临近点算子稳定点，也称P-稳定点，即如果存在拉格朗日乘子λ^*∈，∈和常数γ₁，γ₂>0，满足

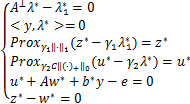.(17)

这里的=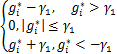，其中g^*:=z^*-γ₁，[Pro(h^*)]_i=，其中h^*:=u^*-γ₂λ^*。

3　算法及收敛性分析

本节设计相应的算法(L_0/1-SSVM)求解该模型，并对算法进行收敛性分析

3.1　算法

对于模型(16)，相应的增广拉格朗日函数为

L_σ(w，b，z，u，λ，λ₁)

=‖z‖₁+C+

　<λ，u+Aw+by-e>+

　<λ₁，z-w>+‖u+Aw+by-e‖²+

　‖z-w‖²，

其中λ∈，λ₁∈是拉格朗日乘子，σ>0是罚参数。

为简化求解，令v=λ₁为缩放对偶变量，则缩放后的ADMM的增广拉格朗日函数为

L_σ(w，b，z，u，λ，v)

=‖z‖₁+C+<λ，u+Aw+by-e>+

‖u+Aw+by-e‖²+‖z-w+v‖².

对应的ADMM迭代框架如下

u^k⁺¹=argL_σ(w^k，b^k，z^k，u，λ^k，v^k)，

z^k⁺¹=argL_σ(w^k，b^k，z，u^k⁺¹，λ^k，v^k)，

w^k⁺¹=argL_σ(w，b^k，z^k⁺¹，u^k⁺¹，λ^k，v^k)+

，

b^k⁺¹=argL_σ(w^k⁺¹，b，z^k⁺¹，u^k⁺¹，λ^k，v^k)，

λ^k⁺¹=λ^k+ησ(u^k⁺¹-e+Aw^k⁺¹+b^k⁺¹y)，

v^k⁺¹=v^k+η(w^k⁺¹-z^k⁺¹).(18)

其中η>0是对偶步长，近端项‖w-w^k=<w-w^k，V_k(w-w^k)>，由于w-子问题是强凸的，因此V_k为一个不定矩阵。

每个子问题的具体迭代过程如下:

(1)u-子问题的迭代

u-子问题可以表示为

u^k⁺¹=argC+

利用定义，得到u的迭代如下:

u^k⁺¹=Pro(e-Aw^k+b^ky-).(19)

(2)z-子问题的迭代

z-子问题可以表示为

z^k⁺¹=arg‖z‖₁+‖z-w+v‖².

0∈∂=σ(z-w+v)+∂‖z‖₁即-σ(z-w+v)=∂‖z‖₁=t_i，其中

t_i=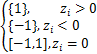，i=1，…，m.

结合之后进行化简归类，可以得到

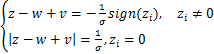令r^k=w^k-v^k，得到z的迭代如下:

z^k⁺¹=()=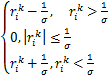.(20)

(3)w-子问题的迭代

w-子问题可以表示为

w^k⁺¹=arg<λ，Aw>++

‖u+Aw+by-e‖²+‖z-w+v‖².

w-子问题是一个关于w的凸规划问题，即有

0=A^⊥λ^k-σ(w-w^k)+

σA^⊥(u^k⁺¹+Aw+b^ky-e)-σ(z^k-w+v^k).

得到w的迭代如下:

(I+)w^k⁺¹=
A^⊥.(21)

(4)b-子问题的迭代

b-子问题可以表示为

b^k⁺¹=arg<λ，by>+‖u+Aw+by-e‖².

得到b的迭代如下:

b^k⁺¹=.(22)

(5)更新λ

λ的更新如下

λ^k⁺¹=λ^k+ησ(u^k⁺¹+Aw^k⁺¹+b^k⁺¹y-e).(23)

(6)更新v

v的更新如下

v^k⁺¹=v^k+η(w^k⁺¹+z^k⁺¹).(24)

根据以上迭代规则，给出L_0/1损失稀疏支持向量机的ADMM算法迭代框架:

算法(L_0/1-SSVM)

初始化 w⁰∈，z⁰∈，u⁰∈，b⁰∈R，λ⁰∈，v⁰∈;

循环 for k =0:MaxIter do

步1　通过公式(19)计算u^k⁺¹;

步2　通过公式(20)计算z^k⁺¹;

步3　通过公式(21)计算w^k⁺¹;

步4　通过公式(22)计算b^k⁺¹;

步5　通过公式(23)更新λ^k⁺¹;

步6　通过公式(24)更新v^k⁺¹;

步7　当满足终止条件(17)时迭代停止，否则置k=k+1，转步1。

输出 (w，b)

3.2　收敛性分析

定理3　假设(w^*，b^*，z^*，u^*，λ^*，v^*)为序列{(w^k，b^k，z^k，u^k，λ^k，v^k)}通过算法ADMM生成的极限点，那么(w^*，b^*，z^*，u^*)是一个P-稳定点，而且是问题(16)的局部最优解。

证明:设h^k:=e-Aw^k-b^ky-，由于V_k=以及其补集:=\V_k，因此V_k⊆有有限多个元素，对于足够大的k，有子集J⊆{1，2，3，…}使

V_j≡:V　∀j∈J.

为了表示简单，设Λ^k:=(w^k，b^k，z^k，u^k，λ^k，v^k)及其极限点Λ^*:=(w^*，b^*，z^*，u^*，λ^*，v^*)，即{Λ^k}→Λ^*，这也表示{Λ^j}_j_∈J→Λ^*和{Λ^j⁺¹}_j_+1∈J→Λ^*。

(1)将λ^k在J处取极限，即k∈J，k→¥，有

由上式可知+A+y-e=0

(2)将u^k在J处取极限，即k∈J，k→¥，有

h^*=e-Aw^*-b^*y-

=[e-Aw^*-b^*y-u^*]+u^*-.

又由L_0/1近端算子的定义有

因此由(b)和=0有

==[e-A-y-]+-

=[e-A-y-]+.

可以得出e-A-y-=0，

又因为+A+y-e=0，

得到u^*+Aw^*+b^*y-e=0，即h^*=u^*-，

因此由L_0/1近端算子的定义有

u^*=Pro(h^*)=Pro.

(3)将v^k在J处取极限，即k∈J，k→¥，有

v^*=v^*+σ(z^*-w^*).

得到z^*-w^*=0。

(4)将z^k在J处取极限，即k∈J，k→¥，有

z^*=Pro(w^*-v^*)=Pro(z^*-v^*).

(5)将w^k在J处取极限，即k∈J，k→¥，有

(I+A_V)w^*

=A_Vw^*-+z^*+v^*.

即w^*+w^*A_V=A_Vw^*-+z^*+v^*，有0=-+v^*，由于v^*=，得到

-=0.

(6)将b^k在J处取极限，即k∈J，k→¥，有

b^*=

=b^*-.

得到<y，λ^*>=0。

综上所述(w^*，b^*，z^*，u^*)是一个P-稳定点，而且是问题的局部最优解，证明完成。

4　总结与展望

4.1　总结

本文建立了一个基于L_0/1损失函数，使用l₁范数作为正则项的稀疏支持向量机(L_0/1-SSVM)，给出了模型的一阶最优性条件，包括解的性质，模型的KKT点、P-稳定点以及与全局最优解的关系。提出相应的ADMM算法，通过l₁范数的临近点算子推导出子问题的迭代表达式，并证明算法是收敛的。

4.2　展望

本文对L_0/1稀疏支持向量机进行了一定的研究，但仍不太完善，在模型方可以使用更稀疏的l₀范数作为正则项，还可以拓展到n维空间，建立基于L_0/1损失的稀疏支持张量机等;对于模型的二阶最优性条件也可以作深入研究;本文在数值实验方面的研究有所欠缺，可以将其应用于实际问题，验证算法的有效性。

利益冲突: 作者声明无利益冲突。

^{^[①]} *通讯作者　Corresponding author:高彩霞，smsgcx@imu.edu.cn
收稿日期:2024-04-11;　录用日期:2024-05-22;　发表日期:2024-09-28

参考文献(References)

[1] Boyd S, Parikh N, Chu E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends' in Mac-hine learning, 2011, 3(1): 1-122.
https://doi.org/10.1561/2200000016.
[2] Chartrand R. Exact reconstruction of sparse signals via nonconvex minimization[J]. IEEE Signal Processing L-etters, 2007, 14(10): 707-710.
https://doi.org/10.1109/LSP.2007.898300.
[3] Wright J, Ma Y, Mairal J, et al. Sparse representation for computer vision and pattern recognition[J]. Proceedings of the IEEE, 2010, 98(6): 1031-1044.
[4] Liu J, Chen J, Ye J. Large-scale sparse logistic regression[C]. Proceedings of the 15th ACM SIGKDD international conference on Knowledge discovery and data mining, 2009: 547-556.
https://doi.org/10.1145/1557019.1557082.
[5] Bienstock D. Computational study of a famliy of mixedinteger quadratic programming problems[J]. Mathematical programming, 1996, 74: 121-140.
https://doi.org/10.1007/BF02592208.
[6] Zou H, Hastie T, Tibshirani R. Sparse principal component analysis[J]. Journal of computational and graphical statistics, 2006, 15(2): 265-286.
https://doi.org/10.1198/106186006X113430.
[7] Cortes C, Vapnik V. Support-vector networks[J]. Machine Learning, 1995, 20: 273-297.
https://doi.org/10.1007/BF00994018.
[8] Schölkopf B, Smola A J. Learning with kernels: support vector machines, regularization, optimization, and beyond [M]. MIT press, 2002.
https://doi.org/10.1198/jasa.2003.s269.
[9] Elad M, Figueiredo M A T, Ma Y. On the role of sparse and redundant representations in image processing[J]. Proceedings of the IEEE, 2010, 98(6): 972-982.
https://doi.org/10.1109/jproc.2009.2037655.
[10] Bartlett P L, Wegkamp M H. Classification with a Reject Option using a Hinge Loss. Journal of Machine Learning Research, 2008, 9(8).
[11] Jumutc V, Huang X, Suykens J A K. Fixed-size Pegasos f-or hinge and pinball loss SVM[C]. The 2013 International Joint Conference on Neural Networks(IJCNN). IEEE, 2013: 1-7.
https://doi.org/10.1109/ijcnn.2013.6706864.
[12] Shen X, Tseng G C, Zhang X, et al. On psi-Learning[J]. Journal of the American Statistical Association, 2003, 98(1): 724-734.
[13] Wang H, Shao Y, Zhou S, et al. Support Vector Machine Classifier via L0/1Soft-Margin Loss[J]. IEEE transactions on pattern analysis and machine intelligence, 2021, 44(10): 7253-7265.
https://doi.org/10.1109/TPAMI.2021.3092177.
[14] Zhu J, Rosset S, Tibshirani R, et al. 1-norm support vector machines[J]. Advances in neural information processing systems, 2003, 16.
[15] Tanveer M, Sharma S, Rastogi R, et al. Sparse support vector machine with pinball loss[J]. Transactions on Emerging Telecommunications Technologies, 2021, 32(2): e3820.
https://doi.org/10.1002/ett.3820.
[16] Zheng Q, Zhu F, Qin J, et al. Sparse support matrix machine[J]. Pattern Recognition, 2018, 76: 715-726.
https://doi.org/10.1016/j.patcog.2017.10.003.
[17] Wen F, Adhikari L, Pei L, et al. Nonconvex regularization- based sparse recovery and demixing with application to color image inpainting[J]. IEEE Access, 2017, 5: 11513-11527.
https://doi.org/10.1109/access.2017.2705646.
[18] Shao Y H, Li C N, Huang L W, et al. Joint sample and feature selection via sparse primal and dual LSSVM[J]. Knowledge-Based Systems, 2019, 185: 104915.
https://doi.org/10.1016/j.knosys.2019.104915.
[19] Makela M M, Neittaanmaki P. Nonsmooth optimization: analysis and algorithms with applications to optimal control[M]. 5th Edition. World Scientific, 1992.
[20] 赵晨, 罗自炎, 修乃华. 稀疏优化理论与算法若干新进展[J]. 运筹学学报, 2020, 24(4): 1-24.
https://doi.org/10.15960/j.cnki.issn.1007-6093.2020.04.001.

Optimality Conditions and Algorithms for Sparse Support Vector Machines with l1 Regular Terms

YANG Xiaohui, GAO Caixia^*

(School of Mathematical Sciences, Inner Mongolia University, Hohhot 010021, China)

Abstract: Support Vector Machine (SVM) , as one of the main methods of machine learning, is a popular learning tool used to solve classification and regression tasks, and has attracted much attention in the fields of image classification, pattern recognition and disease diagnosis. In the context of the support vector machine model (SVM) , the loss function is considered optimal, with most existing loss functions acting as proxies. Since l1 norm has good sparsity, redundant features can be removed through feature selection. In this paper, a loss-based norm sparse support vector machine (called L0/1-SSVM) is proposed based on the L0/1 soft margin loss model. The existence of the model solution is proved, the KKT points and P-stable points of the model are given, and the relationship between the global optimal solution and KKT points is proved. The iterative framework of ADMM algorithm is designed by using the proximal operator of l1 norm, and the convergence analysis is carried out to prove that the algorithm converges to the P-stable point.

Keywords: l1 norm, L0/1 loss function, sparse support vector machine, optimality conditions, ADMM algorithm

DOI: 10.48014/fcpm.20240411001

Citation: YANG Xiaohui, GAO Caixia. Optimality conditions and algorithms for sparse support vector machines with l1 regular terms[J]. Frontiers of Chinese Pure Mathematics, 2024, 2(3): 16-24.