加权Kuramoto模型稳定性的理论分析及数值验证-HTML全文-中国理论数学前沿-科学足迹出版社(SFP)

加权Kuramoto模型稳定性的理论分析及数值验证

张志昊, 许润泽, 徐艺荥, 邹委员^*

(北京化工大学数理学院, 北京 100029)

摘要: 本文系统研究了Kuramoto振子模型在复杂网络同步动力学中的理论拓展与工程应用。作为经典动力学模型, Kuramoto模型广泛用于揭示复杂系统中的集体振荡行为及其同步机制, 对生物节律、神经网络和化学振荡等领域的同步现象具有重要意义。首先, 本文系统回顾了Kuramoto方程的核心结构、发展历程以及临界耦合强度Ke的必要条件。在此基础上, 本文提出了考虑质量偏差的加权网络 Kuramoto模型, 并从理论上推导出质量偏差对系统同步行为的约束条件, 证明在特定初始条件下, 模型的同步阈值对质量扰动具有鲁棒性。通过数值模拟验证, 该模型在耦合强度K的限制下展现出显著的同步特性, 且质量偏差对同步特性的影响有限。本研究为揭示复杂网络系统的同步行为提供了新的理论框架, 并在电力系统稳定性分析、神经动力学建模和分布式协同控制等实际工程应用中具有重要意义。

关键词: Kuramoto 模型, 同步现象, 鲁棒性, 数值模拟

DOI: 10.48014/fcpm.20250502002

引用格式: 张志昊, 许润泽, 徐艺荥, 等. 加权Kuramoto模型稳定性的理论分析及数值验证[J]. 中国理论数学前沿, 2025, 3(2): 4-12.

文章类型: 研究性论文

收稿日期: 2025-05-02

接收日期: 2025-06-07

出版日期: 2025-06-28

1　前言

同步现象广泛存在于自然与社会系统中。而Kuramoto模型是描述这类现象的经典数学模型之一，该模型为研究集体振荡行为提供了重要的理论框架^[1^]，尤其针对振子在单位圆周上的相互作用及其同步条件进行了深入分析。该模型在生物节律学、神经网络和化学振荡等领域具有重要的理论与应用价值^[2^]。通过Kuramoto模型，可以理解和预测大规模振荡系统中的同步现象，这对阐释生物系统中的协调行为以及解决网络通信中的同步问题具有重要意义。在科学研究中，应用该模型有助于揭示自然界复杂系统的动力学规律，为解决实际问题提供了重要的理论依据和指导^[3^]。

1.1　Kuramoto方程介绍

1975年，日本物理学家藏本由纪首次提出了著名的Kuramoto模型^[1^]。该模型最初旨在描述化学和生物振子的动态行为，但后来被发现具有广泛的应用价值。模型假设所有振子完全相同，且彼此之间的耦合较弱;任意两个振子之间的相互作用强度取决于它们相位差的正弦函数^[4^]。Kuramoto方程的微分形式表达为:

=Ω_i-sin(θ_i-θ_j)，i∈{1，…，n}(1.1)

所有振子都在单位圆周(S¹)上运动，它们仅具备一个自由度，运动状态完全由其角位置θ所确定。是该振子角位置对时间的导数，即角速度。角速度的变化反映了振子在相位空间中的动态演化过程。Ω_i是该振子的固有频率，表示在没有外部耦合影响下振子的自然振荡频率。K是耦合强度，其数值直接影响系统的同步行为。临界同步耦合强度(通常记为K_e)是系统从无序状态过渡到全局同步状态的关键参数，确定K_e的值以及影响其变化的因素是该领域研究的核心课题之一。自从Kuramoto于1975年首次提出该模型以来，关于临界耦合强度的研究取得了重大进展。最初的研究集中在具有均匀分布频率的全局耦合振子系统，通过自洽分析得到了K_e的解析表达式。随后，Dörfler，Florian Anton^[5^]将模型推广到具有分布式固有频率的异质性振子系统，探讨了频率分布形状对同步过程的影响。近年来，随着复杂网络理论的发展，Kuramoto模型被进一步扩展到复杂网络拓扑结构上。研究发现在不同的网络结构(如小世界网络、无标度网络、随机网络)上，临界耦合强度K_e会受到网络连接模式的显著影响。此外，引入耦合时滞、随机扰动以及多重耦合机制等因素，对K_e的影响也成为热点研究方向。通过确定临界同步耦合强度K_e，可以实现对实际系统同步行为的预测与控制。n是振子总个数，sin(θ_i-θ_j)代表其他振子对该振子的总影响因子。

1.2　Kuramoto方程的发展历程

近年来，国内外学者对 Kuramoto 模型的研究取得了重要进展，特别是在高维系统、复杂网络拓扑和随机扰动下的同步问题方面。2014年，在第三十三届中国控制会议上，朱建东等^[6^]建立了一个限制在光滑曲面上的高维 Kuramoto 模型。他们推导了系统平衡点的必要和充分条件，并对平衡点周围的系统进行了线性化分析。由于所考虑的光滑曲面为椭球体，研究得到了系统的一些动力学特性，包括极限行为和不稳定性。基于这些结果，实现了几乎全局的同步，并通过数值模拟验证了理论结果。2018年，Ha及其合作者^[7^]针对惯性Kuramoto模型，提出了一个理论框架，揭示了系统从一般初始配置向相位锁定松弛时经历三个阶段:迅速形成包含多数振荡子的巨型簇;巨型簇吸引其余振荡子;系统渐近达到相位锁定。他们通过对序参量演化的估计，推导了相位和频率的有界性。2023年，朱婷婷^[8^]探讨了具有阻滞的Kuramoto模型的离散时间动力学。对于离散的同质Kuramoto模型，在初始配置限定于半圆内的情况下，给出了系统同步的指数收敛估计。针对非同质振荡器，通过对原始模型进行二阶提升，研究了相应的离散增强模型的涌现行为。在足够大的耦合强度和较小的步长条件下，证明了当初始配置位于四分之一圆的小区域内时，系统将收敛到频率同步。同年，Cho及其合作者^[9^]针对惯性Kuramoto模型，提出了一个理论框架，揭示了系统从一般初始配置向相位锁定松弛时经历三个阶段:迅速形成包含多数振荡子的巨型簇;巨型簇吸引其余振荡子;系统渐近达到相位锁定。2024 年，熊和浪等^[10^]针对一类网络拓扑时变且耦合通道存在随机干扰的 Kuramoto型振子网络的同步问题，设计了事件触发机制下的固定时间控制算法。他们的工作考虑了实际网络中通信资源有限和随机扰动存在的情况，通过理论分析和数值模拟，证明了所提算法的有效性和鲁棒性。

这些成果充分展示了国内学者在 Kuramoto 模型领域的深入探索和创新，不仅为复杂网络系统的同步控制理论提供了全新的思路和方法，也为电力系统稳定性、神经科学以及协同控制等实际应用中同步现象的理解和实践提供了重要的理论支持。

1.3　Kuramoto方程的改进

传统的 Kuramoto 模型假定所有振子的结构和参数完全相同，比如拥有相同的质量、固有频率和耦合特性。然而，在实际物理系统中，振子的质量、阻尼系数以及其他参数通常存在细微差异，这就使得传统 Kuramoto 模型在描述真实系统同步现象时存在一定局限。因此，为了解决这一问题，我们研究了当振子质量存在微小偏差ò时的情形。首先，我们推导了考虑质量偏差修正后的 Kuramoto 模型动态方程，并对质量微扰对系统同步行为的影响进行了详细分析。通过严格的数学证明，我们得到:在初始相位和固有频率处于合理范围内时，Kuramoto模型的临界耦合强度对振子质量的微小偏差具有鲁棒性，即同步阈值基本不受影响。主定理明确限定了初始条件的合理范围，确保了结论的有效性。在选取满足定理条件的初值后，我们通过数值模拟进一步验证了理论分析。模拟结果显示质量轻微变化对同步行为影响极小，与质量一致时几乎相同，验证了模型同步特性的稳定性与可靠性。

2　基本Kuramoto方程临界耦合K值

2.1　Kuramoto模型的基本符号

除1.1中提到的基础符号以外，本文还将使用一些简单记号。

2.1.1　相位符号

相位极大值、相位极小值、相位直径与相位初值分别定义为:

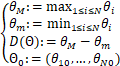(2.1)

2.1.2　自然频率符号

自然频率向量与自然频率直径分别定义为:

(2.2)

2.1.3　频率符号

记频率=ω，并且频率极大值，频率极小值，频率直径分别定义为:

(2.3)

2.1.4　临界耦合强度K_e

临界同步耦合强度(通常记为K_e)是系统从无序状态过渡到全局同步状态的关键参数，本文主要研究临界耦合强度K_e值的情况。

2.2　K值下界必要性定理

在已知的研究工作中，已有多种临界耦合强度K_e的判断方法，本文将引用文献^[11^]中的如下引理:

引理1^[¹¹^]:如果K</2，∀i，j∈{1，…，n}，那么方程(1.1)不存在同步解(t)=(t)。

证明:假设存在这样的同步解，代入方程即可得到:

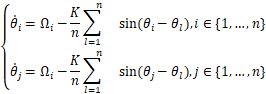
则:

≥

与题设矛盾。故不存在同步解(t)=(t)。

2.3　由频率直径引导的临界耦合强度

在考虑临界耦合强度时，文献^[11^]中给出如下引理:

引理2^[¹¹^]:如果D(Ω)>0，K>K_e=D(Ω)，sinD(Θ₀)<。则

在更一般的权网络微扰情况下，我们将推广这个引理，以扩大其适用范围。

2.4　本文的重要结果

对引理2中进一步推广，本文将会得到两个核心结论，并在第四部分中加以证明:

命题3:若D(Ω)>0，K>K_e=，则

D(Θ(t))<D₂

命题3描述了在权网络Kuramoto模型中相位稳定的充分条件，在权网络Kuramoto模型中相较于引理2更具一般性。

命题4:若D(Ω)>0，K>K_e=，则

相较于Dörfler ^[5^]，本文在引理2的基础上进行改进，放宽了振子质量相等的假设，考虑了振子间的微小质量差异。基于此，引入了权网络Kuramoto模型，证明了在此条件下临界耦合强度的变化，并给出了频率直径的收敛描述。该命题是引理2的改进。

最后，本文针对这两个命题进行了数值模拟，得到了在不同ò和N的情况下相位和频率的状态，并画出了三维图，直观地展示了上述两条命题。

综上，本文创新性地证明了Kuramoto模型在权网络结构下仍保持良好的鲁棒性，并通过数值模拟清晰地展示了这一点，这一研究为实际系统中的集体振荡行为提供了重要的理论支持和应用价值。

2.5　本文结构

在该小节之前，主要叙述已有文献的基本工作，第二节剩余部分，将证明放缩基本定理以便后续证明，并进行数值模拟验证前文引理2。第三节提出了变质量的Kuramoto模型，构建了权重网络系统，并说明构建权重网络系统的必要性与重要性。第四节展示了本文的核心命题，即权重网络系统的鲁棒性，并列出了相关参数，进行了详细证明。第五节通过数值模拟验证了理论分析结果的正确性。最后分析变质量的Kuramoto模型可能的未来实际应用。

2.6　放缩基本定理

对于相位非线性项sin(θ_i-θ_j)，我们通过缩放方法转化非线性项，这需要应用一个放缩定理，该定理确保在缩放过程中各项保持一致性和可比性:

定理5:对相位非线性项sin(θ_i-θ_j)，∀j∈{1，…，n}，有如下放缩成立:

sin(θ_j-θ_m)-sin(θ_j-θ_M)≥sinD(Θ) (2.4)

证明:设f(x)=，f在 [-π，π] 中无最大值，只有上确界 f(x)=1。

θ_j-θ_m≥0，　θ_j-θ_m≤D(Θ)

θ_j-θ_M≤0，　θ_j-θ_M≥-D(Θ)

那么由f的性质得到:

≥

≥=

则

sin(θ_j-θ_m)≥(θ_j-θ_m)

sin(θ_j-θ_M)≤(θ_j-θ_M)

两式相减，即得:

sin(θ_j-θ_m)-sin(θ_j-θ_M)≥sinD(Θ)

该定理有效地化解了非线性项求和所引发的繁琐分析，为后续定理的严密证明奠定了坚实基础。

2.7　Kuramoto原始模型数值模拟

我们使用MATLAB进行数值模拟，采用如下算法结构并作图:

算法步骤1:随机生成一系列振子，其中振子的数量从10到30个，并设置模拟的时间区间为从0到100个单位时间，步长为1。设置振荡器自然频率的均值为 0，设置振荡器自然频率的标准差为 1。

算法步骤2:根据引理2，设置耦合强度K>D(Ω)=8，通过数值求解，我们获得了振子相位随时间变化的对应关系。结果表明，所有振子在极短的时间内便实现了相位稳定和频率同步。

算法步骤3:在时间取值充分大的情况下观察微分方程的解，在允许误差范围内可认为其频率直径为零，即所有振子均实现了频率同步，从而验证了引理2的结论。

算法步骤4:以时间t为x轴，粒子数量N为y轴，相位(频率)直径D(Θ)(D()) 为z轴进行作图，以观察系统的同步效果(见图1)，结果显示，随振子数量的增加，同步性的结论并未受到明显影响。

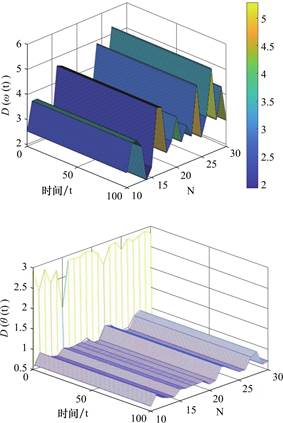
图1　频率(相位)与t，N的关系

Fig.1　Relationship between frequency(phase)and t，N

3　权网络系统研究

3.1　权网络系统引入

在实际的物理模型中，振子的质量通常存在差异，这使得在描述此类非均匀系统的动力学行为时给传统的 Kuramoto 模型带来了挑战。具体而言，质量不同的振子对其他振子施加的作用力与其质量成正比，这是由于振子间的相互作用会受到质量的影响。然而，当系统中振子的数量非常庞大时，个体振子质量的微小偏差ò对整体系统的动力学影响在以往的研究中往往忽略不计，注意到这样不加证明而直接忽略偏差的行为是欠妥的。因此，为了更精确地刻画具有质量差异的振子系统，有必要对经典的Kuramoto模型进行适当的改进，以考虑振子之间质量的微小差异对系统行为的影响。如果能够证明振子间微小的质量差异仅在可控范围内影响系统行为，那么这项工作将具有重要意义。事实上，本文不仅证明了这一点，还通过数值模拟进行了验证。

对方程(1.1)做微小权重扰动，得到变质量Kuramoto模型，又称为权网络扰动Kuramoto模型:

=Ω_i-ψ_ijsin(θ_i-θ_j)，
i∈{1，…，n}(3.1)

其中，d_i(Ψ)=ψ_ij。

方程(7)中存在结构性假设:

≤ò

这些ò被视为扰动常数。由于系统中振子的数量通常极为庞大，个体振子质量的微小偏差的平均值必然趋近于零，因此ò的数值相对较小。

3.2　权网络临界值变动

设定新的耦合强度为 K=，我们将证明该值为系统的临界耦合强度K_e。由于ò很小，因此该临界耦合强度与非加权网络Kuramoto 模型的临界值相差不大。我们将在后续的数值模拟中验证这一结论。

4　权网络结构基本原理

对于权网络扰动Kuramoto模型(3.1)，我们分别研究它的相位直径与频率直径。

4.1　相位直径上界

考虑方程sinx=+2ò，由于sinx∈，在K>K_e=的情况下，它在上必然有两解，分别设为D₁，D₂且D₁≤D₂。

我们先证明一个集合不变性引理:

引理3:设集合

A:={Θ∈[0，2π)^N:D(Θ)<D₂}(4.1)

则

Θ₀∈A⇒Θ(t)∈A，∀t>0

证明:

记T:={T∈[0，¥)|D(Θ(t))<D₂，∀t∈[0，T)}.

设T^*=supT.证明分成两步:

(i)T 非空:

Θ₀∈A⇒Θ(t)∈A，∀t>0

由于Θ₀∈A，D(Θ(t)) 连续，存在T>0，∀t∈[0，T)，

D(Θ(t))<D₂

由上，T非空，T^*>0。

(ii):=¥.

建立微分不等式，对方程求导可以得到，并联合(2.4):

D(Θ(t))=Ω_M-Ω_m+

≤D(Ω)+

≤D(Ω)++

2Kò≤D(Ω)-Ksin(D(Θ(t)))+2Kò，

因为 D(Θ(t))<D₂<π，t∈[0，T^*)，我们有:

sin(D(Θ(t)))≥(D(Θ(t)))

然后，联立得到

D(Θ(t))≤D(Ω)+

2Kò-K(D(Θ(t)))

解微分不等式，利用Gronwall引理得到:

D(Θ(t))≤

D₂+(D(Θ₀)-D₂)，t∈[0，T^*)

通过令 t→T^* 并利用假设 D(Θ₀)<D₂，我们有:

D(Θ(T^*))<D₂

这样引出矛盾，即T^*并非有限上确界，因此我们有:

T^*=¥，Θ(t)∈A，t≥0

4.2　命题3的证明

根据引理3的结论，D(Θ)<D₂对于∀t∈[0，¥)成立，那么即可证明命题3，该命题是相位直径的上界描述。

4.3　频率分布区域

由上已经得到了权网络结构的相位直径D(Θ)的上界，以此结论证明引理4，控制频率直径D()的频率区域，以此得到频率收敛值。

引理4:若D(Ω)>0，K>K_e=，频率函数由如下不等式控制收敛:

D((t₀))≤D((t))

≤D((t₀))，t≥t₀.

证明:由

D(Θ(t))≤D₂，

我们设

ω_i=，1≤i≤N.

求导得到

=cos(θ_j-θ_i)(ω_j-ω_i)

+Kcos(θ_j-θ_i)(ω_j-ω_i).

而对于直径频率

D(ω(t))=max_1≤k_，l≤N|ω_k-ω_l|:=-.

同样求导得到

D(ω)=(-)

=[cos(θ_k-)(ω_k-)-

cos(θ_k-)(ω_k-)]+

Kcos(θ_k-

)(ω_k-)-K

cos(θ_k-)(ω_k-)

=J₂₁+J₂₂+J₂₃.

对J₂₁，J₂₂，J₂₃分别分析:

对于J₂₁:由于

|θ_k-θ_i|≤D₂.

而事实上，ω_k-≤0，ω_k-≥0，

J₂₁≤[cos(θ_k-)(ω_k-)-

cos(θ_k-)(ω_k-)]

≤-Kcos(D₂)D(ω)，t≥t₀.

再对J₂₂，J₂₃放缩，根据限制条件:

≤，

则

|J_2i|≤KòD(ω)，i=2，3.

于是

D(ω)≤-K(cos(D₂)-2ò)D(ω)，t≥t₀.

根据Gronwall引理，

D(ω(t))≤D(ω(t₀))，t≥t₀.

同理，

D(ω(t))≥-K(1+2ò)D(ω(t))

D(ω(t))≥D(ω(t₀))，t≥t₀.

4.4　命题4的证明

在引理4中，取t→¥，即可得到|(t)-(t)|=0。显然频率是趋于同步的，这就证明了命题4的结论，在理论上证明了同步的一个充分条件。

5　权网络结构数值模拟

5.1　数值作图

在时间t的演变对于频率直径和相位直径影响不大的情况下，舍弃以时间t为x轴，转而使用偏差ò为x轴，粒子数量N为y轴，t足够大时(100个单位时长)的相位(频率)直径D(Θ)(D())为z轴，其中n的范围设置在10~200之间，ò的范围设置在0~0.15之间，为取随机数方便，在K=12附近设置随机数(但仍满足K>11.45)，使用MATLAB中的ode45进行数值模拟，并作图2观察同步效果，特别的，给出N=100时振子的同步情况如图3。

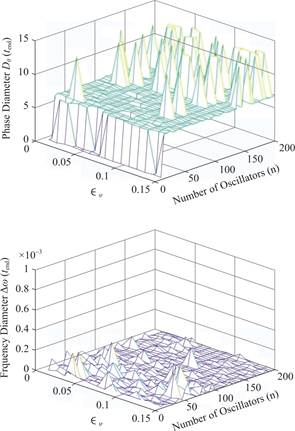
图2　频率(相位)与ò，N 的关系

Fig.2　Relationship between frequency(phase)and ò，N

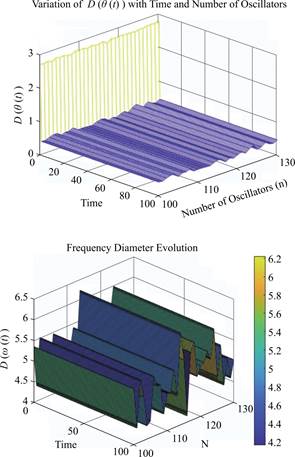
图3　N>100时同步情况

Fig.3　Synchronization situation when N>100

5.2　数值处理与结论

我们使用MATLAB进行数值模拟，采用如下算法结构并作图:

算法步骤1:随机生成一系列随机振子，允许每个振子的“质量”具有略小的差别，我们设定不同振子质量的最高差别上限为ò，并据此计算得到K_e。

算法步骤2:由定理3，4的条件，设定耦合强度K>K_e≈11.45，得到相位解随时间的对应关系，发现所有振子在该耦合强度限制下均呈现相位稳定，频率同步现象。

算法步骤3:在耦合强度的限制下，所有振子的相位直径的一个上界为D₂，均满足相位直径上界性质，验证了命题3的结论。

算法步骤4:在时间取值充分大的情况下观察微分方程的解，观察到在允许的误差范围内(小于0.001)，可以认为频率直径为零，即所有振子实现了频率同步，验证了命题4的结论。

算法步骤5:随振子数量增加，在N=10之后，作图3验证本文结论在大规模网络中的普适性。探究得到以上结论仍然不受显著影响。

6　近期研究结论对比与分析

在近期Kuramoto 模型研究中，Ha等^[12^]研究者特别探讨了渐近同步如何在同步因素(如强耦合强度)与去同步因素(如惯性和挫折)的竞争中出现。提出了若干基于系统参数和初始配置的框架，这些框架保证了完全同步的涌现。较于Ha^[12^]相等研究者的结果，本论文立足于系统中振子质量的微小差异，研究在权网络结构下完全同步的涌现。是不同物理情境下对完全同步出现情况的探求。

7　未来与展望

本文针对加权网络上的 Kuramoto 模型进行了研究，尽管通过理论证明和数值模拟得出了相位稳定和频率同步的结果，但该模型尚未在实际应用中得到充分验证，其对变质量振子运动的解释力仍存在一定的局限性，且实际问题更具复杂性和一般性。因此，在未来的研究中，可以考虑在现有 Kuramoto 框架的基础上，引入非线性耦合、时滞效应、随机扰动等因素，以更贴近实际系统中常见的复杂现象。通过对这些因素的系统引入与分析，可以构建出更为丰富且具有广泛适用性的同步模型，从而扩展其在各类实际场景中的应用范围。

利益冲突: 作者声明无利益冲突。

^{^[①]} *通讯作者　Corresponding author:邹委员，zwy@amss.ac.cn
收稿日期:2025-05-02;　录用日期:2025-06-07;　发表日期:2025-06-28

参考文献(References)

[1] Y. KURAMOTO. Self-entrainment of a population of coupled non-linear oscillators[M]//International Symposium on Mathematical Problems in Theoretical Physics. Berlin: Springer Berlin Heidelberg, 1975.
[2] Y. P. CHOI, S. Y. HA, S. JUNG, et al. Asymptotic formation and orbital stability of phase-locked states for the Kuramoto model[J]. Phys. D, 2012, 241: 735-754.
https://doi.org/10.1016/j.physd.2011.11.011
[3] J. BUCK, E. BUCK. Biology of synchronous flashing of fireflies[J]. Nature, 1996, 211: 562-564.
[4] Y. KURAMOTO. Chemical Oscillations, Waves, and Turbulence[M]. Tokyo: Springer-Verlag, 1984.
[5] F. A. DÖRFLER. Dynamics and Control in Power Grids and Complex Oscillator Networks[D]. Santa Barbara: University of California, Santa Barbara, 2013.
[6] J. D. ZHU. Kuramoto Model on Smooth Curved Surfaces of High-dimensional Spaces[C]//中国自动化学会控制理论专业委员会, 中国系统工程学会. 第三十三届中国控制会议论文集(D卷). 上海: 上海系统科学出版社, 2014: 6.
[7] S. Y. HA, H. KIM, J. PARK. Remarks on the complete synchronization for the Kuramoto model with frustrations[J]. Anal. Appl. , 2018, 16: 525-563.
https://doi.org/10.1142/S0219530517500130.
[8] T. T. ZHU. On the synchronization of discrete-time Kuramoto model with frustration[J]. Communications on Pure and Applied Analysis, 2023, 22(11): 3233-3249.
https://doi.org/10.3934/cpaa.2023109.
[9] H. CHO, J. G. DONG, S. Y. HA, et al. Emergent dynamics of the inertial Kuramoto model in a large coupling regime[J]. Communications in Partial Differential Equations, 2023, 49(1-2): 1-30.
https://doi.org/10.1080/03605302.2023.2300824.
[10] 熊河浪, 张华. 非均匀Kuramoto振子系统的频率同步[J]. 重庆理工大学学报(自然科学), 2021, 35(08): 230-236.
[11] S. Y. HA, Y. KIM, Z. LI. Large-Time Dynamics of Kuramoto Oscillators under the Effects of Inertia and Frustration[J]. SIAM Journal on Applied Dynamical Systems, 2014, 13(1): 466-492.
https://doi.org/10.1137/130926559.

Theoretical Analysis and Numerical Verification of Stability in Weighted Kuramoto Models

ZHANG Zhihao, XU Runze, XU Yiying, ZOU Weiyuan^*

(School of Mathematics and Physics, Beijing University of Chemical Technology, Beijing 100029, China)

Abstract: This paper systematically studies the theoretical advancements and engineering applications of the Kuramoto oscillator model in the synchronization dynamics of complex networks. As a classical dynamical model, the Kuramoto model is widely utilized to uncover collective oscillatory behaviors and synchronization mechanisms in complex systems, demonstrating significant implications for the synchronization phenomena observed in domains such as biological rhythms, neural networks, and chemical oscillations. Firstly, this paper provides a comprehensive review of the core structure of the Kuramoto equations, the historical progression of its development, and the critical coupling strength Kc necessary for synchronization. Building upon this foundation, this article proposes a weighted network Kuramoto model that considers mass disparity, and theoretically derives the constraints of quality deviation on system synchronization behavior. It proves that under specific initial conditions, the synchronization threshold of the model exhibits robustness against mass perturbations. Numerical simulations further verify that the model displays remarkable synchronization patterns under restricted coupling strengths K , while the impact of mass disparity on synchronization properties remains limited. This research offers a novel theoretical framework for elucidating the synchronization behavior. of complex network systems and holds significant practical relevance for applications in power system stability analysis, neural dynamics modeling, and distributed cooperative control in engineering contexts.

Keywords: Kuramoto model, synchronization phenomena, robustness, numerical simulation

DOI: 10.48014/fcpm.20250502002

Citation: ZHANG Zhihao, XU Runze, XU Yiying, et al. Theoretical analysis and numerical verification of stability in Weighted Kuramoto Models[J]. Frontiers of Chinese Pure Mathematics, 2025, 3(2): 4-12.