基于多目标机器学习模型的城市内涝快速模拟研究

赖成光^1,2, 廖耀星¹, 王兆礼^1,2,*, 陈晓宏³

(1. 华南理工大学土木与交通学院, 广州 510641
2. 人工智能与数字经济广东省实验室 (广州) , 广州 510330
3. 中山大学水资源与环境研究中心, 广州 510275)

摘要: 近年来频发的城市暴雨内涝灾害已给国家造成了严重的经济损失和人员伤亡。内涝数值模拟是灾害预警预报及防控的一种重要手段, 然而传统的数值物理模型存在计算效率低下的缺点, 难以满足暴雨内涝实时模拟和预警预报需求。为此, 本研究结合具有物理机制的耦合雨洪模型和机器学习算法各自的优势, 提出基于多目标机器学习算法的城市暴雨内涝淹没水深快速模拟的方法, 分别探讨了K近邻 (KNN) 、多目标随机森林 (MORF) 、极端梯度提升 (XGBoost) 及其集成模型的预测性能, 结果表明: (1) 基于SWMM和LISFLOOD-FP构建的耦合雨洪模型在研究区暴雨内涝模拟中具有良好的适用性, 在此基础上共生成了70种包含不同特征的“暴雨内涝”数据库; (2) KNN、MORF、XGBoost及其集成模型的水深预测效果均较好, 皮尔逊相关系数 (PCC) 值均达0. 812以上, 平均绝对误差 (MAE) 均在6. 9cm以下, 均方根误差 (RMSE) 不超过0. 116; KNNMORF-XGBoost集成模型的总体效果最好, 其MAE、PCC和RMSE的平均值分别为2. 4cm、0. 965和0. 043; (3) 所构建的多目标机器学习预测模型除了预测精度高外, 其预测速度极快, 水深模拟效率比耦合雨洪模型提升20倍以上。本研究可为机器学习在城市暴雨内涝快速模拟方面提供一种新思路, 对内涝灾害的预警预报具有重要价值。

关键词: 城市内涝, 耦合雨洪模型, 机器学习, 多目标预测, 快速模拟

DOI: 10.48014/fcws.20220827001

引用格式: 赖成光, 廖耀星, 王兆礼, 等. 基于多目标机器学习模型的城市内涝快速模拟研究[J]. 中国水科学前沿, 2023, 1(1): 1-16.

文章类型: 研究性论文

收稿日期: 2022-08-29

接收日期: 2022-11-06

出版日期: 2023-03-28

0　引言

受全球气候变化以及城市化影响，因暴雨造成的内涝灾害频繁发生，给国家和社会造成了难以估量的损失^[1,2]，如2021年郑州的“7·20”、2020年广州的“5·22”、2012年北京的“7·21”等典型事件均给当地造成了重大的人员伤亡和经济损失。内涝灾害的预警预报是减少灾损的重要非工程措施，而利用雨洪模型对暴雨内涝开展快速模拟是当前预警预报工作的重要一环，其精度、广度和深度会深刻影响预警预报的实施效果。

自20世纪以来，国内外学者陆续开发了一系列雨洪模型^[3]，其中城市雨洪管理模型(SWMM)得到最为广泛的应用，已被大量应用于暴雨内涝预警预报、市政管网设计、低影响开发雨洪效应分析等领域^[4]。由于SWMM模型无法模拟二维淹没情况，学者们尝试将SWMM模型与LISFLOOD-FP、TELEMAC-2D、WCA2D等二维水动力模型结合起来构建可实现一维、二维精细化模拟的耦合雨洪模型^[5-7];然而，这些耦合模型存在模拟时间较长的缺点^[8]，即便采用GPU加速等高性能计算技术仍难以实现大范围、高精度的快速模拟^[9,10]。由于城市内涝对预报的时效性要求极高，这些基于明确物理机制的耦合模型显然也难以满足内涝灾害的实时预报与预警的要求，为此，一些机器学习算法被陆续引入来弥补模型模拟效率低下的缺陷。

机器学习算法具有强大的数据处理能力和高效的计算效率，在洪涝数值模拟和快速预测方面已展现出巨大潜力^[11]，特别是在一维径流预测方面应用广泛^[12,13]，如Panda等^[13]利用3个月的小时水位数据训练了人工神经网络(ANN)预测模型，发现ANN模型在水位和峰值预测精度上均优于MIKE11模型。然而，相对于一维径流模拟，由于二维淹没模拟与预测的输入和输出数据量大大增加，特征变量增多且映射关系更复杂，如何结合机器学习算法开展内涝的二维快速模拟是当前研究的热点和难点。当前利用机器学习算法开展二维洪涝淹没快速模拟主要通过两类方法实现，第一种称为两阶段方法^[14]，即先预测部分水深点后再对水深进行二维空间扩展，如Jhong等^[15]利用FLO-2D模型构建了降雨淹没的数据库，然后利用支持向量机(SVM)预测点水深，并插值扩展到近邻的空间;然而，通过部分水深点扩展生成空间水深的方法产生的误差较大，实际应用效果较差。第二种方法是在第一种方法的基础上，对逐个网格构建单独的预测模型并直接对每个网格的水深进行预测，如Chu等^[10]和Lin等^[16]分别对研究区内的每个网格构建ANN模型，然后通过大量的ANN模型实现淹没水深的快速预测，预测精度比第一种方法大大提高;然而，这种通过建立大量神经网络模型预测多个网格水深的方法需要设置大量参数，且仍存在训练速度慢和耗时长的问题。

事实上，为了避免对逐个网格构建单独的预测模型，可将内涝淹没的二维预测转化为多目标预测问题，通过引入多目标算法，利用单个模型同时预测多个目标网格的水深，从而减少预测模型的复杂度^[17]。目前多目标算法在煤层厚度预测^[18]、页岩气产量预测^[19]、度量学习^[20]等方面均取得良好效果。然而，利用多目标机器学习算法开展城市内涝模拟与预报的研究目前还未见报道，因此开发一种更高效的基于多目标机器学习的二维水深快速预测方法具有重要价值。

综上，传统的雨洪模型是在明确的物理机制基础上开展数值模拟的，但存在计算效率低下的问题;基于数据驱动的机器学习模型具有数据处理能力强和计算效率高的优点，其计算需要大量的训练样本，但历史灾害样本数据往往十分稀缺。因此，本研究拟结合具有明确物理机制的耦合雨洪模型和机器学习算法的各自优势，以广州市长湴地区为例，耦合SWMM和LISFLOOD-FP构建雨洪模型并生成“暴雨-内涝”数据库，利用不同的多目标机器学习算法构建暴雨内涝预测模型，实现基于降雨输入下内涝淹没水深的快速模拟。本研究可为暴雨内涝灾害快速模拟和灾害预警预报提供新思路。

1　研究区与数据

长湴研究区位于粤港澳大湾区广州市，总面积约为1.61km²(图1)。研究区北部的土地利用类型为山区，南部为高度城市化地区，住宅、道路和商业建筑比例较高。在强降雨期间，大量水从北部山区流入排水渠，导致长湴地铁站周边频繁发生内涝。

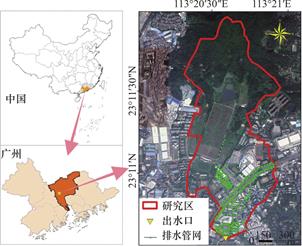
图1　研究区区位及遥感影像图

Fig.1　Location of the study area and the remote-sensing image map

所用数据包括土地利用类型、分辨率为8m×8m和5m×5m的数字高程模型(简称DEM8和DEM5)和排水管网，分别来源于广州市规划和自然资源局。广州市五山站1954—2012年逐时暴雨资料来源于广东省气象局;2018年6月7—8日逐5min实测暴雨数据来源于广州市气象局;遥感影像通过ArcGIS软件对谷歌地图进行截取。对于高程数据，在计算SWMM模型的子汇水区坡度时采用DEM8，DEM5因精度更高则用于内涝的二维精细化模拟。

2　研究方法

基于多目标机器学习的城市内涝快速模拟流程通过以下步骤实现:首先，利用耦合雨洪模型模拟不同暴雨重现期和雨型条件下的淹没情况，以0.01m水深条件判断淹没区和非淹没区，并对模拟的水深栅格数据进行读取并转成二维数组格式;其次，将暴雨内涝数据集划分训练集和测试集，以降雨过程为输入、不同目标网格为输出，分别利用KNN、MORF和XGboost模型进行训练和测试，经过超参数优化后形成多目标水深预测模型并建立集成预测模型;最后，在任意暴雨事件的输入下，利用多目标机器学习水深预测模型快速计算各网格的淹没水深，并最终获得暴雨内涝淹没水深和淹没范围。具体实现流程见图2。

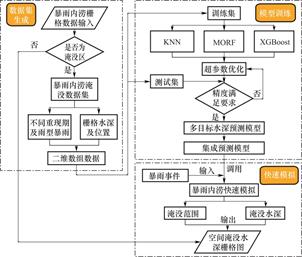
图2　暴雨内涝快速模拟流程图

Fig.2　Flow chart of rapid simulation of rainstorm waterlogging

2.1　耦合雨洪模型

暴雨洪水管理模型(SWMM)于1970年代由美国环保署开发，用于模拟单次或连续降雨下的水量和水质的模型^[21]。该模型是分布式水文水动力模型，通过地表产流汇流、地下水、融雪、流量及地表积水等过程模拟水文、管网水动力变化过程。SWMM模型中的数学计算模块包括地表产流、汇流和管网汇流等模块。LISFLOOD-FP模型是由英国布里斯托尔大学于2000年开发的基于栅格的洪水模拟模型^[22]，经过不断更新和完善，2013年8月已经升级到5.9版本。该模型包括两大核心求解器，分别是一维河道求解器和二维洪泛区求解器，对应模拟洪水沿河道和洪泛区的传播，模型主要基于连续性方程和动量方程进行洪涝淹没模拟。

尽管SWMM模型自带管网汇流模块，但缺乏地表漫流模块，导致无法提供详细的淹没范围和水深信息。LISFLOOD-FP无法考虑管网汇流信息，但能根据给定的溢流信息模拟积水在地表的运动，可提供径流的时空演变信息。基于两个模型的优势，对模型进行耦合，由SWMM模型导出溢流过程后输入LISFLOOD-FP模型进行积水二维模拟，最后模拟暴雨淹没水深和空间分布。具体耦合过程详见曾照洋等^[7] 的研究。

2.2　暴雨过程设计

由于缺乏实测降雨内涝资料，因此本研究采取设计暴雨输入雨洪模型当中。输入具有当地实际降雨特征的暴雨过程对提高暴雨内涝数据库的代表性具有重要作用。为此结合当地历史暴雨资料共设计7种雨型:Ⅰ型为单峰峰前，Ⅱ型为单峰峰后，Ⅲ型为单峰峰中，Ⅳ型为均匀雨型，Ⅴ型为双峰一前一后，Ⅵ型为双峰靠前，Ⅶ型为双峰靠后，具体设计过程见Zhang等^[23]的研究。除以上7种雨型外，还采用了芝加哥雨型作为对比，并设置3种不同雨峰系数(0.3、0.48和0.7)。

结合以往研究经验，本次模拟暴雨时长取2h;分别选取1a、2a、5a、10a、20a、50a和100a共7种暴雨重现期，其中各重现期下2h总降雨量是根据广州市水务局2018 年 9 月印发的《广州市排水管理办法实施细则》中的暴雨强度公式推算。最后，考虑不同雨型特征条件下共设计了70种暴雨情景，具体暴雨过程如图3所示。

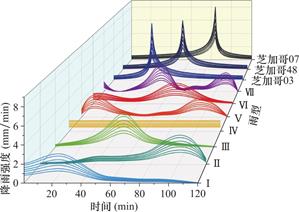
图3　不同重现期和雨型特征暴雨分配过程

Fig.3　Rainfall distribution process with different recurrence periods and rainfall pattern characteristics

2.3　多目标机器学习模型

本研究分别采用KNN、MORF和XGboost三种机器学习方法构建内涝淹没水深预测模型。

(1)K近邻模型(KNN)

KNN算法是传统的非参数回归预测方法，既可以解决单目标问题，也可以解决多目标问题。KNN通过寻找训练集中与预测值特征向量最相似(最近邻)的K个样本来进行预测。如果所需预测的样本与该训练集中K个最相似的样本中的绝大多数都属于某一类别，则预测样本也属于该类别。相似性是用两个样本(每个样本包含n个数据)之间的距离度量来定义，最常见的是欧几里得距离。

(2)多目标随机森林(MORF)

随机森林(RF)是由Breiman于2001年提出的一种基于统计学习理论的集成学习算法^[24]。其主要利用Bootstrap方法从训练数据中抽出多个样本，并对每个样本构建回归树，对所有回归树的预测结果进行集合并得出最终结果。传统的随机森林通常只有单个目标，仅能预测单个变量^[25]。为了实现多个目标的同时输出和预测，多目标随机森林(MORF)被进一步提出^[26]。多目标随机森林的子模型是多目标回归树。假设训练集T有L个实例，包括m个特征的预测变量X_j，…，X_m和d个目标的目标变量Y_j，…，Y_d;实例l中的输入向量x^(l)=(，…，，…，)，多目标输出向量y^(l)=(，…，，…，)。其中，i∈(1，…，m)，j∈(1，…，d)，l∈(1，…，L)。

在单目标回归树中，节点t的不纯度i(t)被定义为^[27]:

(1)

式中，y_k和(t)分别为目标变量的值和目标变量在节点t处的平均值，N_t是节点t上的数据点数。

设一个预测变量X_p将父节点t在分割点c拆分为t_L和t_R两个子节点。由于预测变量X_p 分割点c分裂导致节点t的不纯度减少值Δi(c，t的计算如下^[25]:

Δi(c，t=i(t)-i(t_L)-i(t_R)(2)

式中，和分别为左节点t_L和右节点t_R中的数据个数。

从单目标回归树到多目标回归树的方法是将单变量响应替换为多变量响应，即通过对多变量响应上的单变量不纯度累加重新计算节点的不纯度，如式(3)所示^[28]:

(3)

式中，表示节点中第j个目标下y^(l)的平均值，选择不纯度总和最小值作为节点的最终分割点。最后，利用随机选择特征构建基于多目标回归树的多目标随机森林模型。

(3)极端梯度提升(XGBoost)

XGBoost算法由Chen等^[29]于2016年提出，是从梯度提升决策树(GBDT)算法衍生而来的改进模型。XGBoost算法通过对损失函数进行二阶泰勒展开并且添加正则项，有效地避免了过拟合同时加快了收敛的速度。该算法的基本思想为不断地添加树和进行特征分裂，每添加一棵树就学习一个新的函数，以每一轮的预测去拟合上一轮预测的残差，根据样本的特征就可预测样本分数。XGBoost算法可以表示成一种加法的形式，如式(4)所示。

(4)

式中，表示模型的预测值;k表示决策树的数目;f_k表示第k个子模型;x_i表示第i个输入样本。

2.4　集成预测模型

为降低耦合雨洪模型与机器学习模型造成的累计误差，在机器学习的基础上进一步构建各模型的误差校正模型^[30]。本研究以降雨为输入，误差矩阵为输出构建误差校正模型。同时，为了降低单个模型的不稳定性及不确定性，构建4个基于KNN、MORF、XGBoost的组合集成模型，包括KNN-MORF模型、KNN-XGBoost模型、MORF-XGBoost模型和KNN-MORF-XGBoost模型。集成模型的输出由不同模型的输出对决定系数的加权平均得到。

3　结果分析

3.1　城市内涝模型验证与“暴雨-内涝”数据库

在雨洪模型构建过程中，研究区的SWMM模型中的检查井共654个、管线653条、汇水区91个。SWMM模型参数取值参考用户手册^[21]及邻近研究区^[5,31]取值确定。选取广州市2018年6月7—8日的测暴雨资料对SWMM模型进行验证，结果表明出水口(图1)流量变化趋势与降雨的变化总体上相吻合，出水口流量峰现时间均比雨峰时间滞后约5min，与一般城市雨洪规律相符。对于二维模拟验证，模型模拟淹没范围与实测积水范围大致符合;邻近长湴地铁站C出口的淹没水深基本在0.2~0.3m，最大水深达0.47m，模拟结果与现场调研淹没情况相符;此外，淹没模拟结果与团队前期的研究结果基本一致^[4,6,31]。以上表明所构建的耦合雨洪模型合理可靠，可用于后续的暴雨内涝数值模拟。

将2.2节所设计的70种暴雨过程输入耦合雨洪模型中模拟内涝淹没积水情况，淹没结果统计详见赖成光等^[32]的研究成果。统计结果表明，不同暴雨输入条件下的淹没特征有较明显差异，即使在同一重现期下，不同雨型和集中度下所造成的内涝淹没情况也有较大差别，而这些差异对不同暴雨过程导致内涝淹没特征的识别至关重要。由此，基于不同条件下的暴雨输入及其对应的内涝淹没特征构建“暴雨-内涝”的数据库，可为后续多目标机器学习预测模型训练和测试提供基础数据。

3.2　多目标机器学习预测模型训练结果分析

构建“暴雨-内涝”数据库后，利用多目标机器学习模型学习暴雨与淹没水深之间的关系。多目标机器学习模型的自变量为暴雨过程，其中暴雨历时为120min，每分钟为一个变量则共有120个特征变量，不同目标变量为不同空间栅格的淹没水深，本研究中共有5749个网格(目标)。将70种暴雨内涝情景根据8∶2的比例划分为训练集和测试集(其中训练集56个、测试集14个)构建机器学习模型。样本在划分时要尽量保证训练集和测试集数据分布的一致性，以增强数据的代表性和模型的泛化能力。本研究采取随机划分加手动调整的方法使得测试集尽量包含不同的暴雨特征。分别利用KNN、MORF、XGBoost算法以及4个集成模型共构建了7个暴雨内涝预测模型。通过网格搜索法对KNN模型、MORF模型及XGBoost模型的主要参数进行优选。其中，KNN模型的参数K为2，距离度量选择欧式距离;MORF模型回归树的数量取100，用于每个节点二分数据的自变量个数为20，以及树的最大深度为20;XGBoost模型的学习率为0.1，最大深度为20，其他参数为默认参数。此外，对每个机器学习模型进行了误差校正，误差校正模型的参数与上述参数相同。KNN模型、MORF模型和XGBoost模型的R²为分别0.846、0.991和0.954，基于此构建基于决定系数加权的集成预测模型。

3.3　预测模型性能评估结果分析

对7个机器学习模型在14场不同测试暴雨下的水深预测效果进行了评估和对比。14场测试暴雨内涝情景包括100年一遇Ⅳ型，50年一遇Ⅰ型、Ⅵ型、芝加哥型(雨峰0.7)，20年一遇Ⅴ、芝加哥型(雨峰0.3)，10年一遇Ⅲ型、芝加哥型(雨峰0.48)，5年一遇Ⅰ型、Ⅱ型、Ⅶ型，2年一遇Ⅲ型、芝加哥型(雨峰0.3)，1年一遇芝加哥型(雨峰0.48)，这些测试暴雨均未参与模型的训练。

受限于版面空间，仅展示KNN、MORF、XGBoost模型以及KNN-MORF-XGBoost集成模型的预测水深与雨洪模型的模拟水深之间的对比散点密度图(图4~图7)。结果显示各预测模型的水深预测值与雨洪模型模拟的水深均呈显著线性相关关系(P<0.001)，表明这些预测模型能较好预测暴雨内涝情景。图8~图11分别展示了KNN、MORF、XGBoost和KNN-MORF-XGBoost集成模型的预测水深与雨洪模型的模拟水深之间的空间差异，结果表明各预测模型的空间水深与耦合雨洪模型模拟的结果较为接近，最大水深出现位置相符合，二者的最大水深差值较小(基本在10cm以下)。

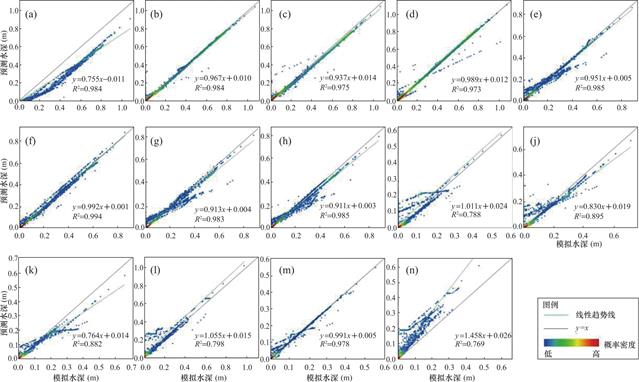
图4　KNN模型预测水深与耦合雨洪模型模拟水深散点对比图((a)~(n)分别表示100年一遇Ⅳ型，50年一遇Ⅰ型、Ⅵ型、芝加哥型(雨峰0.7)，20年一遇Ⅴ型、芝加哥型(雨峰0.3)，10年一遇Ⅲ型、芝加哥型(雨峰0.48)，5年一遇Ⅰ型、Ⅱ型、Ⅶ型，2年一遇Ⅲ型、芝加哥型(雨峰0.3)，1年一遇芝加哥型(雨峰0.48);图中每个散点对应每个空间网格，散点密度值越高代表点越密集;下同)

Fig.4　Scatterplots comparison of the predicted water depth between the KNN model and the simulated water depth o the coupled rainstorm-flood model.(Figures(a)-(n)represents 100-year event type IV;50-year event type I，VI，Chicago type(rain peak 0.7);20-year event type V，Chicago type(rain peak 0.3);10-year event type III，Chicago type(rain peak 0.48);5-year event type I，II，VII;2-year event type III，Chicago type(rain peak 0.3);and 1-year event，Chicago type(rain peak 0.48)，respectively).Each scatter point in the figure corresponds to each spatial grid，and a high scatter density value represents dense points.Similarly hereinafter)

分别采取皮尔逊相关系数(PCC)、平均绝对误差(MAE)和均方根误差(RMSE)三个性能评估指标对7个预测模型的性能进行评估(表1~表3)。结果表明，所有预测模型的PCC值均达到0.812以上，MAE均在6.9cm以下，RMSE不超过0.116。其中，KNN模型的MAE在0.9cm到6.9cm之间，PCC值平均为0.962;均方根误差RMSE平均为0.045。MORF模型的MAE在1.0cm到3.8cm之间，PCC值平均为0.963，RMSE平均为0.046。XGBoost模型的MAE在0.9cm到6.4cm之间，PCC值平均为0.952，RMSE平均为0.06。KNN-MORF-XGBoost集成模型的MAE在1.4cm到3.8cm之间，PCC值平均为0.965，RMSE平均为0.043。由分析可知，KNN-MORF模型、KNN模型和KNN-MORF-XGboost模型的MAE指标效果排名前三;KNN-MORF-XGBoost模型、MORF-XGBoost模型和KNN-MORF模型的PCC指标效果靠前;KNN-MORF-XGBoost模型、KNN-MORF模型和KNN-XGBoost模型的RMSE指标效果较好。在所有预测模型中，KNN-MORF-XGboost模型的整体预测效果最好，测试集MAE、PCC和RMSE的平均值在7个模型中分别排名第三、第一和第一。以上表明，集成模型的水深预测效果比单一模型效果更好，可在一定程度上降低单一模型导致的系统误差。

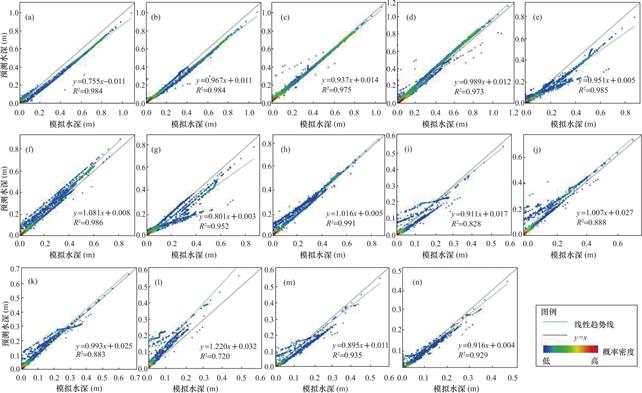
图5　MORF模型预测水深与雨洪模型模拟水深散点对比图

Fig.5　Scatterplots comparison of the predicted water depth between the MORF model and the simulated water depth from the rainstorm-flood model

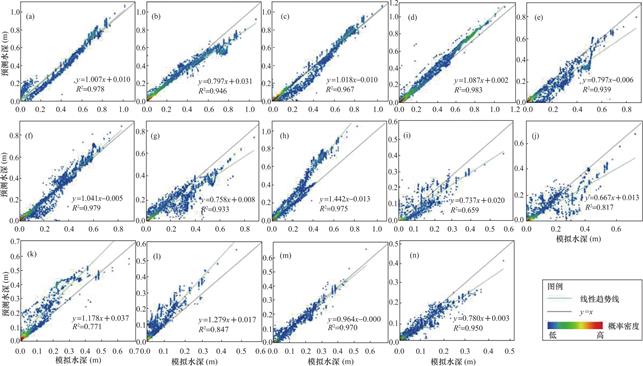
图6　XGBoost模型预测水深与雨洪模型模拟水深散点对比图

Fig.6　Scatterplots comparison of the predicted water depth between the XGBoost model and the simulated water depth from the rainstorm-flood model

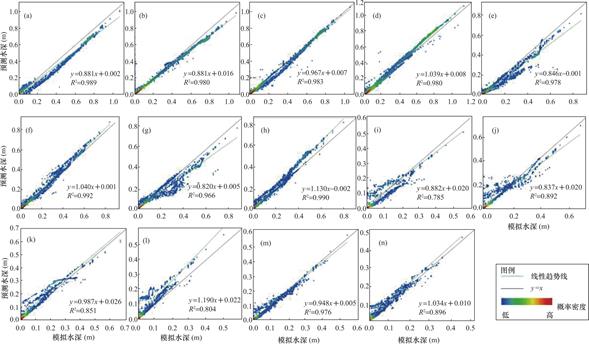
图7　KNN-MORF-XGBoost集成模型预测水深与耦合雨洪模型模拟水深散点对比图

Fig.7　Scatterplots comparison of the predicted water depth between the KNN-MORF-XGBoost integrated model and the simulated water depth from the rainstorm-flood model

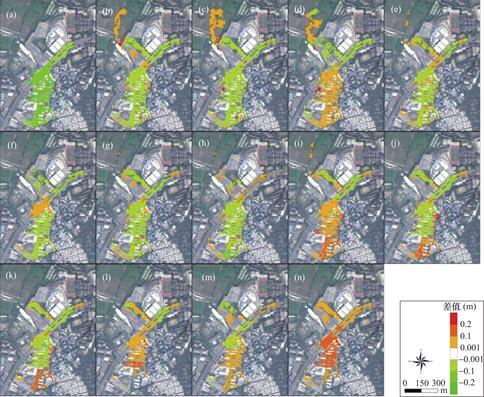
图8　KNN模型预测水深与耦合雨洪模型模拟水深空间差异分布

Fig.8　Spatial difference distribution of inundated water depth predicted by KNN model and simulated water depth by coupled rainstorm-flood model

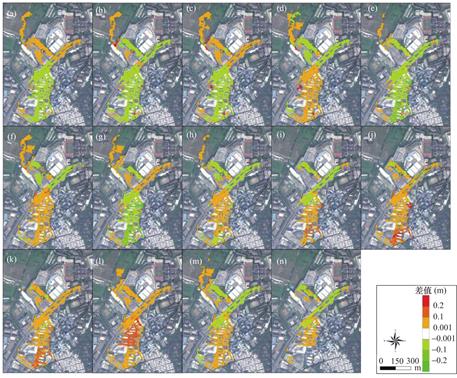
图9　MORF模型预测水深与耦合雨洪模型模拟水深空间差异分布

Fig.9　Spatial difference distribution of inundated water depth predicted by MORF model and simulated water depth by coupled rainstorm-flood model

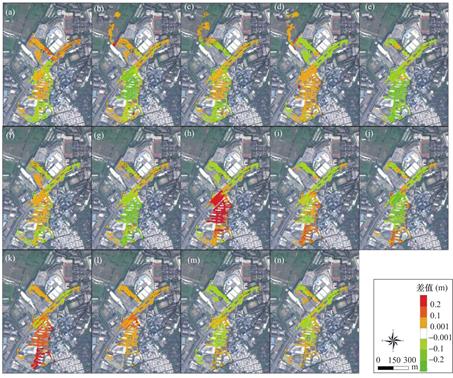
图10　XGBoost模型预测水深与耦合雨洪模型模拟水深空间差异分布

Fig.10　Spatial difference distribution of inundated water depth predicted by XGBoost model and simulated water depth by coupled rainstorm-flood model

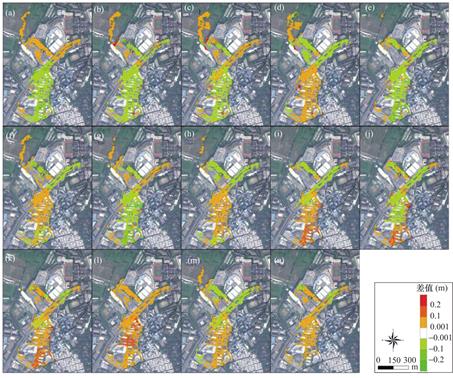
图11　KNN-MORF-XGBoost集成模型预测水深与耦合雨洪模型模拟水深空间差异分布

Fig.11　Spatial difference distribution of inundated water depth predicted by KNN-MORF-XGBoost integrated model and simulated water depth by coupled rainstorm-flood model

表1　各模型空间水深预测指标MAE(m)

Table 1　The MAE values of spatial water depth prediction index of each model(m)

序号	测试 降雨	预测模型
		KNN	MORF	XGBoost	KNN-MORF	KNN-XGBoost	MORF-XGBoost	KNN-MORF-XGBoost
a	100a_Ⅳ	0.069	0.038	0.033	0.051	0.038	0.026	0.038
b	50a_Ⅰ	0.012	0.032	0.046	0.022	0.029	0.037	0.029
c	50a_Ⅵ	0.022	0.020	0.029	0.020	0.020	0.020	0.018
d	50a_zhi07	0.014	0.029	0.035	0.022	0.024	0.031	0.026
e	20a_Ⅴ	0.013	0.035	0.039	0.024	0.025	0.036	0.028
f	20a_zhi03	0.009	0.026	0.018	0.015	0.011	0.018	0.014
g	10a_Ⅲ	0.017	0.036	0.040	0.026	0.028	0.037	0.030
h	10a_zhi48	0.016	0.012	0.064	0.009	0.030	0.036	0.023
i	5a_Ⅰ	0.028	0.022	0.028	0.024	0.026	0.023	0.024
j	5a_Ⅱ	0.025	0.029	0.037	0.021	0.031	0.026	0.025
k	5a_Ⅶ	0.024	0.026	0.051	0.020	0.031	0.038	0.028
l	2a_Ⅲ	0.018	0.038	0.025	0.028	0.021	0.032	0.027
m	2a_zhi03	0.006	0.016	0.008	0.011	0.005	0.010	0.008
n	1a_zhi48	0.042	0.010	0.009	0.022	0.018	0.008	0.014
平均值		0.023**	0.026	0.033	0.023*	0.024	0.027	0.024***

注:带符号*、**、***的加粗值代表预测效果前三的模型。

表2　各模型空间水深预测指标PCC

Table 2　The PCC values of spatial water depth prediction index of each model

序号	测试 降雨	预测模型
		KNN	MORF	XGBoost	KNN-MORF	KNN-XGBoost	MORF-XGBoost	KNN-MORF-XGBoost
a	100a_Ⅳ	0.992	0.997	0.989	0.996	0.992	0.994	0.994
b	50a_Ⅰ	0.992	0.992	0.973	0.992	0.987	0.988	0.990
c	50a_Ⅵ	0.987	0.988	0.983	0.988	0.991	0.991	0.991
d	50a_zhi07	0.986	0.986	0.991	0.986	0.992	0.990	0.990
e	20a_Ⅴ	0.993	0.987	0.969	0.991	0.988	0.983	0.989
f	20a_zhi03	0.997	0.993	0.989	0.996	0.995	0.995	0.996
g	10a_Ⅲ	0.991	0.976	0.966	0.985	0.984	0.976	0.983
h	10a_zhi48	0.992	0.995	0.987	0.996	0.994	0.993	0.995
i	5a_Ⅰ	0.888	0.910	0.812	0.899	0.866	0.881	0.886
j	5a_Ⅱ	0.946	0.942	0.904	0.944	0.938	0.942	0.945
k	5a_Ⅶ	0.939	0.940	0.878	0.941	0.910	0.912	0.922
l	2a_Ⅲ	0.893	0.849	0.920	0.870	0.916	0.895	0.896
m	2a_zhi03	0.989	0.967	0.985	0.981	0.992	0.985	0.988
n	1a_zhi48	0.877	0.964	0.975	0.920	0.935	0.978	0.946
平均值		0.962	0.963	0.952	0.963***	0.963	0.965**	0.965*

注:带符号*、**、***的加粗值代表预测效果前三的模型。

表3　各模型空间水深预测指标RMSE

Table 3　The RMSE values of spatial water depth prediction index of each model

序号	测试 降雨	预测模型
		KNN	MORF	XGBoost	KNN-MORF	KNN-XGBoost	MORF-XGBoost	KNN-MORF-XGBoost
a	100a_Ⅳ	0.107	0.053	0.049	0.077	0.056	0.039	0.054
b	50a_Ⅰ	0.038	0.051	0.084	0.042	0.056	0.063	0.052
c	50a_Ⅵ	0.051	0.050	0.060	0.050	0.043	0.041	0.042
d	50a_zhi07	0.052	0.059	0.059	0.055	0.048	0.055	0.051
e	20a_Ⅴ	0.027	0.058	0.071	0.041	0.045	0.062	0.049
f	20a_zhi03	0.017	0.042	0.036	0.027	0.024	0.031	0.025
g	10a_Ⅲ	0.032	0.062	0.072	0.048	0.051	0.065	0.054
h	10a_zhi48	0.031	0.021	0.116	0.019	0.053	0.063	0.039
i	5a_Ⅰ	0.052	0.039	0.052	0.044	0.048	0.043	0.044
j	5a_Ⅱ	0.048	0.058	0.068	0.050	0.055	0.049	0.048
k	5a_Ⅶ	0.044	0.050	0.094	0.043	0.060	0.070	0.056
l	2a_Ⅲ	0.038	0.063	0.046	0.051	0.040	0.053	0.048
m	2a_zhi03	0.014	0.024	0.016	0.018	0.011	0.016	0.014
n	1a_zhi48	0.073	0.018	0.019	0.040	0.033	0.016	0.026
平均值		0.045	0.046	0.060	0.043**	0.044***	0.048	0.043*

注:带符号*、**、***的加粗值代表预测效果前三的模型。

从模拟时长角度分析，所构建的7个多目标机器学习模型均可在2s内完成研究区每种暴雨情景最大淹没范围及最大淹没水深的预测，而耦合雨洪模型模拟每种情景则需要 48~60s，前者的模拟效率比后者提升20倍以上。可见所构建的多目标机器学习预测模型除了预测精度高外，其计算速度极快，在暴雨内涝快速模拟和内涝灾害预警预报方面具有极大的应用潜力。

4　结语

本研究结合了雨洪模型和机器学习算法的优势，提出了基于多目标机器学习的城市暴雨内涝淹没水深快速预测模拟方法，并探讨了不同多目标机器学习算法的预测性能，得到主要结论如下:(1)基于SWMM和LISFLOOD-FP构建的耦合雨洪模型在研究区的暴雨内涝模拟中呈现良好的适用性，利用该雨洪模型可生成70种具有暴雨不同特征的“暴雨-内涝”数据库;(2)KNN、MORF、XGBoost及集成模型的水深预测效果均较好，所有预测模型的预测水深与耦合雨洪模型的模拟水深的相关性较好，PCC值均达到0.812以上，MAE均在6.9cm以下，RMSE不超过0.116，而空间网格的预测水深与雨洪模型的结果差异基本在10cm以内;集成模型效果比单一模型效果好，KNN-MORF-XGBoost集成模型的水深预测效果最好，其MAE、PCC和RMSE的平均值分别达到2.4cm、0.965和0.043;(3)在模拟效率方面，所构建的多目标机器学习预测模型的预测速度极快，模拟效率比基于物理机制的水耦合雨洪模型提升20倍以上，在暴雨内涝快速模拟和内涝灾害预警预报方面具有极大的应用潜力。

由于缺乏暴雨和内涝实测资料，本研究采用了设计暴雨作为雨洪模型的降雨输入，在实际应用中若有大量实测的暴雨内涝资料输入雨洪模型中，理论上可以进一步提高预测精度。另外，本研究中所构建的机器学习模型对于百年一遇暴雨的内涝预测表现出一定的低估，为解决该问题可以在训练集中可加入更高重现期的暴雨情景，以进一步增加模型的泛化能力。此外，本研究仅考虑了空间普降暴雨下对内涝淹没的快速预测，如何提取降雨的空间特征以实现暴雨时空变化下的内涝快速预测需进一步探讨。由于本研究区总面积约为1.61km²，所构建的基于多目标机器学习的内涝水深预测模型无论是在预测精度和计算效率均呈现出色的性能，然而当研究范围扩大或网格数量大大增加后，这些模型的预测性能是否仍能保持这些优势，后续将会对此继续开展深入探讨。

利益冲突: 作者声明无利益冲突。

---

^[①] *通讯作者　Corresponding author:王兆礼，wangzhl@scut.edu.cn
收稿日期:2022-08-29;　录用日期:2022-11-06;　发表日期:2023-03-28
基金项目:国家重点研发计划项目(2021YFC3001000);国家自然科学基金项目(U1911204; 51879107)。

参考文献(References)

[1] IPCC. Climate Change 2021: The Physical Science Basis [M]. Cambridge: Cambridge University Press, 2021. DOI: 10. 1017/9781009157896
[2] Hallegatte S, Green C, Nicholls R J, et al. Future flood losses in major coastal cities[J]. Nat Clim Change, 2013, 3(9): 802-806.
https: //doi. org/10. 1038/nclimate1979
[3] 徐宗学, 叶陈雷. 城市暴雨洪涝模拟: 原理、模型与展望[J]. 水利学报, 2021, 52(04): 381-392. DOI: 10. 13243/j. cnki. slxb. 20200515
[4] 王兆礼, 陈昱宏, 赖成光. 基于TELEMAC-2D 和 SWMM模型的城市内涝数值模拟[J]. 水资源保护, 2022, 38(01): 117-124. DOI: 10. 3880/j. issn. 1004-6933. 2022. 01. 015
[5] Wu X, Wang Z, Guo S, et al. Scenario-based projections of future urban inundation within a coupled hydrodynamic model framework: A case study in Dongguan City, China [J]. J Hydrol, 2017, 547: 428-442.
https: //doi. org/10. 1016/j. jhydrol. 2017. 02. 020
[6] 曾照洋, 赖成光, 王兆礼, 等. 基于WCA2D与SWMM模型的城市暴雨洪涝快速模拟[J]. 水科学进展, 2020, 31(01): 29-38. DOI: 10. 14042/j. cnki. 32. 1309. 2020. 01. 004
[7] 曾照洋, 王兆礼, 吴旭树, 等. 基于SWMM和LISFLOOD模型的暴雨内涝模拟研究[J]. 水力发电学报, 2017, 36(05): 68-77. DOI: 10. 11660/slfdxb. 20170508
[8] 刘媛媛, 刘业森, 郑敬伟, 等. BP神经网络和数值模型相结合的城市内涝预测方法研究[J]. 水利学报, 2022, 53(03): 284-295. DOI: 10. 13243/j. cnki. slxb. 20210611
[9] Teng J, Vaze J, Kim S, et al. Enhancing the capability of a simple, computationally efficient, conceptual flood inundation model in hydrologically complex terrain[J]. Water Resour Manage, 2019, 33(2): 831-845.
https: //doi. org/10. 1007/s11269-018-2146-7
[10] Chu H, Wu W, Wang Q J, et al. An ANN-based emulation modelling framework for flood inundation modelling: Application, challenges and future directions[J]. Environmental modelling & software: with environment data news, 2020, 124: 104587.
https: //doi. org/10. 1016/j. envsoft. 2019. 104587
[11] Xu T, Liang F. Machine learning for hydrologic sciences: An introductory overview[J]. WIREs Water, 2021, 8(5): e1533.
https: //doi. org/10. 1002/wat2. 1533
[12] Hu C, Wu Q, Li H, et al. Deep learning with a long short-term memory networks approach for rainfall-runoff simulation[J]. Water, 2018, 10(11): 1543.
https: //doi. org/10. 3390/w10111543
[13] Panda R K, Pramanik N, Bala B. Simulation of river stage using artificial neural network and MIKE 11 hydrodynamic model[J]. Comput Geosci, 2010, 36(6): 735-745.
https: //doi. org/10. 1016/j. cageo. 2009. 07. 012
[14] Lin G-F, Lin H-Y, Chou Y-C. Development of a realtime regional-inundation forecasting model for the inundation warning system[J]. J Hydroinf, 2013, 15(4): 1391-1407. DOI: 10. 2166/hydro. 2013. 202
[15] Jhong B-C, Wang J-H, Lin G-F. An integrated twostage support vector machine approach to forecast inundation maps during typhoons[J]. J Hydrol, 2017, 547: 236-252.
https: //doi. org/10. 1016/j. jhydrol. 2017. 01. 057
[16] Lin Q, Leandro J, Gerber S, et al. Multistep flood inundation forecasts with resilient backpropagation neural networks: Kulmbach case study[J]. Water, 2020, 12(12): 3568.
https: //doi. org/10. 3390/w12123568
[17] Kabir S, Patidar S, Xia X, et al. A deep convolutional neural network model for rapid prediction of fluvial flood inundation[J]. J Hydrol, 2020, 590: 125481.
https: //doi. org/10. 1016/j. jhydrol. 2020. 125481
[18] 刘晓明, 王新, 徐慧. 基于多目标随机森林的煤层厚度 同步预测方法[J]. 计算机工程与设计, 2021, 42(04): 1116-1121. DOI: 10. 16208/j. issn1000-7024. 2021. 04. 031
[19] Liang X, Yuetian L, Yifei X, et al. A data-driven shale gas production forecasting method based on the multiobjective random forest regression[J]. Journal of Petroleum Science and Engineering, 2021, 196: 107801.
https: //doi. org/10. 1016/j. petrol. 2020. 107801
[20] Liu W, Xu D, Tsang I W, et al. Metriclearning for multi-output tasks[J]. IEEE transactions on pattern analysis and machine intelligence, 2019, 41(2): 408-422. DOI: 10. 1109/TPAMI. 2018. 2794976
[21] Rossman L A. Storm Water Management Model User's Manual Version 5. 1[M]. Washington DC: USEPA, 2015.
[22] Bates P D, De Roo A P J. A simple raster-based model for flood inundation simulation[J]. Journal of Hydrology, 2000, 236(1): 54-77.
https: //doi. org/10. 1016/S0022-1694(00)00278-X
[23] Zhang M, Xu M, Wang Z, et al. Assessment of the vulnerability of road networks to urban waterlogging based on a coupled hydrodynamic model[J]. J Hydrol, 2021, 603: 127105.
https: //doi. org/10. 1016/j. jhydrol. 2021. 127105
[24] Breiman L. Random forests[J]. Machine Learning, 2001, 45(1): 5-32.
https: //doi. org/10. 1023/A: 1010933404324
[25] Liao Y, Wang Z, Xiong J, et al. Dimming in the pearl river delta of China and the major influencing factors [J]. Clim Res, 2021, 82: 161-176.
https: //doi. org/10. 3354/cr01626
[26] Kocev D, Vens C, Struyf J, et al. Ensembles of Multi- Objective Decision Trees[M]. Berlin, Heidelberg: Springer Berlin Heidelberg, 2007.
https: //doi. org/10. 1007/978-3-540-74958-5_61
[27] Saha D, Alluri P, Gan A. A random forests approach to prioritize Highway Safety Manual(HSM)variables for data collection: Random Forests to Prioritize HSM Variables[J]. J Adv Transp, 2016, 50(4): 522-540.
https: //doi. org/10. 1002/atr. 1358
[28] Borchani H, Varando G, Bielza C, et al. A survey on multi-output regression[J]. WIREs Data Min Knowl Discovery, 2015, 5(5): 216-233.
https: //doi. org/10. 1002/widm. 1157
[29] Chen T, Guestrin C. XGBoost: A Scalable Tree Boosting System [C]. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Francisco, California, USA; Association for Computing Machinery. 2016: 785-794.
https: //doi. org/10. 1145/2939672. 2939785
[30] 周聂, 侯精明, 陈光照, 等. 基于机器学习的山洪灾害快速预报方法[J]. 水资源保护, 2022, 38(02): 32-40, 111. DOI: 10. 3880/j. issn. 1004-6933. 2022. 02. 005
[31] Zeng Z, Wang Z, Lai C. Simulation performance evaluation and uncertainty analysis on a coupled inundation model combining SWMM and WCA2D[J]. Int J Disaster Risk Sci, 2022: 13(3): 448-464.
https: //doi. org/10. 1007/s13753-022-00416-3
[32] 赖成光, 廖耀星, 王兆礼. 不同暴雨雨型条件下的城市内涝响应特征分析[J/OL]. 水资源保护: 1-14[2022- 08-09].
https: //kns-cnki-net. webvpn. scut. edu. cn/kcms/detail/ 32. 1356. TV. 20220801. 1424. 002. html

Fast Simulation of Urban Waterlogging Based on Multi-Objective Machine Learning Model

LAI Chengguang^1,2, LIAO Yaoxing¹, WANG Zhaoli^1,2,*, CHEN Xiaohong³

(1. School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510641, China
2. Artificial Intelligence and Digital Economy Laboratory (Guangzhou) , Guangzhou 510330, China
3. Center for Water Resources and Environment Research, Sun Yat-sen University, Guangzhou 510275, China)

Abstract: The frequent occurrence of urban waterlogging disasters induced by rainstorm has recently caused serious economic losses and casualties in China. Numerical simulation of waterlogging is an important tool for disaster prewarning and forecasting as well as disaster prevention and control; however, the traditional numerical physical models have the disadvantage of low computational efficiency, which makes it difficult to meet the demand for real-time simulation and real-time early warning and forecast. To this end, this study combines the respective advantages of coupled rainstorm-flood models with physical mechanisms and machine learning algorithms, and proposes a rapid prediction and simulation method for inundated depth of urban waterlogging based on multi-objective machine learning algorithms. The forecasting performances of K-Nearest Neighbors (KNN) , Multi-Objective Random Forest (MORF) , Extreme Gradient Boosting (XGBoost) and their integrated models are discussed, respectively. The results show that: (1) The coupled rainstorm- flood model based on SWMM and LISFLOOD-FP has good applicability in the simulation of urban waterlogging induced by rainstorm in the study area. On this basis, the database with a total of 70 scenarios of rainstorm-inundation with different characteristics were generated. (2) The KNN, MORF, XGBoost and their integrated models all have good results in predicting water depth, with Pearson correlation coefficient (PCC) values all above 0. 812, mean absolute error (MAE) below 6. 9 cm, and root-mean-square error (RMSE) less than 0. 116. The KNN-MORF-XGBoost integrated model has the best overall results, with the average values of MAE, PCC and RMSE reaching 2. 4cm, 0. 965 and 0. 043, respectively. (3) In addition to the high prediction accuracy, the prediction speed of the constructed multi-objective machine learning prediction model is extremely fast, and the water depth simulation efficiency is more than 20 times higher than that of the coupled rainstorm-flood model. This study can provide a reference for the application of machine learning in the rapid simulation of urban waterlogging induced by rainstorm, which is of great value for the early warning and forecast of urban waterlogging disaster.  

Keywords: Urban waterlogging, coupled rainstorm-flood model, machine learning, multi- objective prediction, fast simulation

DOI: 10.48014/fcws.20220827001

Citation: LAI Chengguang, LIAO Yaoxing, WANG Zhaoli, et al. Fast simulation of urban waterlogging based on multi-objective machine learning models[J]. Frontiers of Chinese Water Sciences, 2023, 1(1): 1-16.