马克思生产函数思想的延伸探索

张忠任

(日本岛根县立大学, 岛根县 6970016, 日本)

摘要: 从某种程度说, 本文所提出的课题都是全新的尝试, 迄今为止, 尽管不乏利用柯布-道格拉斯生产函数对马克思经济理论所试图进行的某种重新诠释, 但是鲜见从生产函数的角度对马克思主义经济学所进行的系统研究。本文揭示了马克思在《资本论》中具有生产函数思想的明确证据, 并强调在《资本论》中并不存在用字母写成的所谓马克思价值等式c +v +m =w这种表述方式, 而《资本论》第三卷中第一次出现的公式W =c+v +m则属于典型的线性生产函数格式。由此还可以认识到纵向的Leontief生产函数其实源于对马克思生产函数中可变资本部分的分解。在研究方法上, 本文基于对生产函数从特殊到一般的研究所取得的多方系列研究成果, 在阐明了马克思生产函数的基本特征为一种线性生产函数之后, 通过将其拓展为CES生产函数形式而实现了一般化, 从而明确了马克思线性生产函数与其他形式生产函数的内在联系。本文的意义主要在于, 通过探索和分析马克思的生产函数思想, 可以加深对马克思经济理论的认识, 特别是可以进一步拓展源于再生产图式的经济增长模型, 并且有利于与其他学派的经济理论进行对比分析。

关键词: 马克思生产函数, CES生产函数, VES生产函数, 线性齐次生产函数, 欧拉定理

DOI: 10.48014/jce.20231111002

引用格式: 张忠任. 马克思生产函数思想的延伸探索[J]. 中国经济研究, 2024, 3(2): 18-29.

文章类型: 研究性论文

收稿日期: 2023-11-11

接收日期: 2024-03-19

出版日期: 2024-06-28

1　源于古典政治经济学者的生产函数思想

熊彼特(1954)指出，生产函数的最初思想可以追溯到法国重农学派重要的代表人物之一杜尔阁(Anne Robert Jacques Turgot，1727—1781)关于收益递减规律的阐述^[1]:在当等量的资本——劳动数量在这里也是一样——连续投在一块土地上时，则每一次投下资本所得到的产量，开始是不断增加，一直到达增产量与资本增量之比为最大的一点，但是超过这一点后，再投下等量的资本，所得的增产量就会不断下降。这个渐减的增量数列最后必趋近于零。对于这一种最后被认为是真正的收益递减法则的陈述。不过，熊彼特并没有给出他得出这一结论的根据。

斯坦利(1993)明确了杜尔阁关于收益递减规律(law of diminishing returns)的阐述发表于1767年^[2]。杜尔阁的叙述大意如下(译自法文):地球的肥力就像弹簧一样，人们通过连续加载相同的重量来努力弯曲它。如果这个重量很轻并且弹簧不是很灵活，那么第一个负载的作用可能几乎为零。当重物足够强大以克服第一个阻力时，可以看到弹簧以合理的方式屈服并弯曲;但是，当它弯曲到某个点时，它就会产生抗力，会开始抵抗施加在它上面的压力，以前会导致一英寸凹陷的重物现在几乎不能让它移动一根发丝。总之效果会越来越小^[3]。注意。这一论述并未收入杜尔阁的名著《关于财富的形成和分配的考察》(原文为法语:Réflexions sur la formation et la distribution des richesses，1770)一书^[4]之中。

熊彼特(1954)还指出，杜尔阁列举了1900年左右美国经济学家所说的“比例变化法则”的一个特殊例子。这一法则也可以用不同的概念，以稍稍不同的方式来表达。并说这一法则出现于19世纪末，现在叫作“生产函数”，表示产品数量和以不同比例配合起来的生产要素数量之间的技术关系。不过，他在该书中并没有明确指出“生产函数”的概念究竟是谁提出来的。经考证，“生产函数”的概念是1894年最早由英国经济学家菲利普·亨利·维克斯蒂德(Philip Henry Wicksteed，1844—1927)所提出来的^[5]。维克斯蒂德还给出了生产函数的表达式:

不过，杜尔阁从收益递减规律出发的生产函数是基于农业所考虑的。据深山明(2013)考证，经德国经济学家欧根·施马伦巴赫(Eugen Schmalenbach，1873—1955)和康拉德·梅勒罗维奇(Konrad Mellerowicz，1891—1984)的认可，把杜尔阁的生产函数推广到了工业^[6]。

熊彼特(1952)还指出，杜尔阁的生产函数特别巧妙的地方在于，在收益递减的阶段前插进了收益递增的阶段。也就是说承认了一个事实，即收益递减并不是从投下第一副可变生产要素的剂量以后立即就起作用的，而是在达到某一点以后才开始起作用的^[7]。

杜尔阁的生产函数只有一个变量(劳动)。可以通过以下设定并画图来予以解释。令为“农业产出”(纵轴);为“劳动投入”(横轴)，则杜尔阁的生产函数可用来表示。在收益递增区间(如图2-1所示，)，一阶导数大于零即;在收益递减区间(如图2-1所示，)，一阶导数大于零(参见下图)^[8]。

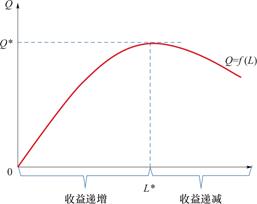
图2-1　杜尔阁的生产函数示意图

Fig.2-1　Schematic diagram of production function of Duerge

一般说来，n个变量的生产函数，可以表述为

如果一个生产函数满足如下条件(>0)，称为规模收益不变:

如果一个生产函数满足如下条件(>0)，称为规模收益递增:

如果一个生产函数满足如下条件(>0)，称为规模收益递减:

如果一个生产函数对于某一常数，满足如下条件(>0)，称为固定规模收益:

生产函数主要有3种类型，线性生产函数、指数生产函数以及固定比例生产函数，我们会在后文中按照顺序陆续介绍。这些类型最终又都被CES生产函数所统一，我们将在本文最后一节讨论这个问题。

下面来考虑生产函数的等产量曲线。

所谓等产量曲线(Isoquant)，指在技术水平不变的条件下，生产同一产量的两种生产要素投入量的不同组合所产生的轨迹。等产量曲线与原点的距离的远近体现表示产量水平的高低，离原点越远代表产量越大。

注意:等产量曲线所反映的是实物量关系，属于本书第5章第4节所涉及过的技术效率问题。

按照投入的生产要素之间相互替代的程度，可以把等产量曲线划分为三种类型。

当投入生产要素之间存在不完全替代关系，等产量曲线的形状一般为向原点凸出的曲线。

如果把也算作一维，则成为一个曲面。

当投入生产要素之间完全可以替代，等产量曲线的形状则是一条直线，可如下图所示:

当投入要素之间完全不能替代，等产量曲线的形状是一条直角线，此时为固定投入比例生产函数。也就是说，在每一个产量水平上任何一对要素投入量之间的比例都是固定的(意味着技术不变)。假定生产过程中只使用和两种要素，则固定投入比例生产函数的通常形式为:，其中， 和 通常作为和的生产技术系数，表示生产1单位产品所需要的固定的和的投入量。

图2-2　不完全替代假定下的等产量曲线(本图用Excel做成)

Fig.2-2　Equal yield curve under the assumption of incomplete substitution

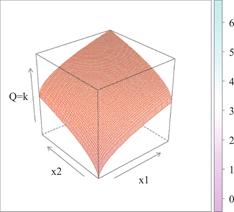
图2-3　不完全替代假定下的等产量曲面(本图用R语言做成^[②])

Fig.2-3　Equal yield surface under the assumption of incomplete substitution

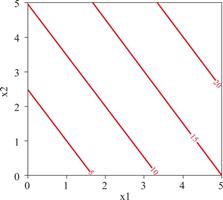
图2-4　完全替代假定下的等产量曲线^[③]

Fig.2-4　Equal yield curve under the assumption of complete substitution

图2-5　固定投入比例生产函数的等产量曲线

Fig.2-5　Equal output curve of fixed input proportion production function

对于固定投入比例生产函数来说，当生产要素都增加倍时，

所以固定投入比例生产函数是规模报酬不变的。

设可微生产函数为:，对其取全微分，在同一条等产量线上有:

2　齐次生产函数

如果生产函数满足:，(其中0)，则该生产函数被称为阶齐次生产函数。

当时， 被称为规模收益不变的生产函数(规模收益不变的生产函数意味着当投入扩大倍的时候，产出也相应地扩大倍);当>1，时，则被称为规模收益递增生产函数;当>1，时，则为规模收益递减生产函数。被称为齐次度(degree of homogeneity)。齐次度的生产函数被称为次齐次生产函数。

齐次生产函数是一种很特殊的生产函数，具有很多特点。特别是，规模收益不变的齐次生产函数满足欧拉定理(Euler􀆳s Theorem)，其含义是:在完全竞争条件下，假设长期中规模收益不变，则全部产品正好足够分配给各种生产要素。所以此定理也被称为“产品分配净尽定理”(英语一般使用:Euler’s Theorem of Distribution)。其数学含义是，对于任意1次齐次生产函数，有

我们以两个变量的1次齐次生产函数为例来说明欧拉定理^[9]。假设表示资本，表示资本劳动，则意味着资本的边际产品，而是劳动的边际产品。

因为对于任意生产函数，按照全微分的规则有

于是欧拉定理可以按照这种方法证明，在许多西方经济学教科书中都有，其中一个简易证明是:假定存在一个1次齐次生产函数，令，则，从而，接着分别对和求偏导数，注意，，可得:

对上述两式求和可得:

表明，总产品正好等于总量(资本的边际产品乘以资本的数量)加上相应的资本总量(劳动的边际产品乘以劳动力的数量)

一般意义下的欧拉定理这样考虑的:对于任意齐次度的生产函数即次一般齐次生产函数来说，也就是在(其中)的条件下，有^[④]

其证明如下。因为

令，，，对等式两端的求偏导数得:

注意:，，因此有

取，或者取极限令，则得到所需要证明的结果。

例题:为7次齐次生产函数。

因为

所以有

即满足欧拉定理。

3　线性的马克思生产函数

通常，都把称为马克思的价值等式，这种说法并没有问题，因为马克思用数字来表述的这种关系，比比皆是，尤其在《资本论》第二卷当中。不过，恐怕很少会有人知道，在《资本论》中，并不存在用字母写成的等式。用字母写成的此等式左端部分的第一次出现在《资本论》第一卷中^[10]，马克思的用法是“它的价值=c+v+m”。请注意这种用法，因为式的部分在等式的右端。

在《资本论》第三卷中才第一次出现了

(3-1)

这种表述方式^[11]，但却不是，两者的含义是不同的。只是一个等式，而(2-1)则是一种典型的生产函数的表述方式，而且是一种齐次的二元线性生产函数(Linear Production Function)。马克思有时为了分析的方便，也曾假定不变资本部分等于零。于是，预付资本就从简化为，产品价值c+v+m就简化为价值产品^[12]。这时，马克思生产函数就简化为

(3-2)

线性生产函数是生产函数的一种形式，通过线性关系描述了投入和产出之间的线性关系^[⑤]。最简单的一元线性生产函数只有一种投入，可以表示为:，它显示了一种比例关系，其图形是一条通过原点的直线。如果投入表示劳动，则意味着劳动生产率，可表述为:

而一般的多元线性生产函数可表述为:

当常数项的时候则为齐次线性生产函数。此时，由于

所以，齐次线性生产函数是规模收益不变的。

为了分析的方便，我们来考虑两个变量的线性齐次生产函数，对于任意，有。

令，，，，

注意:，，，，，所以有

全部产品恰好足够分配给两种生产要素(即)。

如果令剩余价值率为e，(3-1)可以改写成

(3-3)

同样，(3-2)可以改写成

(3-4)

显然有

或者

从这里也可以看出，作为线性生产函数的马克思生产函数是规模报酬不变的。

下面我们来证明马克思生产函数满足欧拉定理。为此，分别对公式(3-4)中的和求偏导数可得:

从而可知:

需要注意的是，就是资本有机构成。从短期来看，可以假定资本有机构成不变，则马克思生产函数等产量线就是属于固定投入比例生产函数那种直角线。如果以可变资本为横轴，以不变资本为纵轴，则资本有机构成就是马克思生产函数的扩展线的斜率。^[⑥]

不过，从长期来看，在马克思那里，不变资本和可变资本是具有可替换性的^[13]。因为不变资本和可变资本之间存在的是不完全替代关系，所以等产量曲线的形状一般为向原点凸出的曲线。此时，过扩展线上某一点的切线的斜率就是资本有机构成。

如果把也算作一维，则成为一个曲面(平面)。

图3-1　马克思生产函数的等产量曲线(本图用R语言做成^①)

Fig.3-1　Equaloutput curve of Marx􀆳s production function

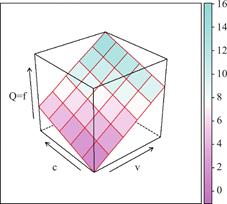
图3-2　马克思生产函数的等产量曲面(本图用R语言做成^②)

Fig.3-2　Equaloutput surface of Marx’s production function

4　马克思生产函数的指数化

日本经济学者大西广通过对柯布-道格拉斯生产函数(简称C-D 生产函数)重新定义，建立起指数型马克思生产函数。为此，我们先阐述一下柯布-道格拉斯生产函数。

C-D生产函数是由Charles Wiggins Cobb(1875-1949)和Paul Howard Douglas(1892-1976)在1928年根据统计数据验证而确立的^[14](C-D 生产函数)被广泛用于表示两种或多种投入(特别是资本和劳动)的数量与产出数量之间的技术关系。其一般表达式为^[⑦]:

这里:^[⑧]

Y=总产出(1年)

L=劳动投入(1年工作人时)

K=资本投入(机器、设备和建筑物等)

A=全要素生产率

参数α和β分别是资本和劳动的产出弹性，是由技术确定的常数，相当于总产出对生产中所投入的劳动或资本水平变化的反应的灵敏度，例如当α=0.75时，意味着劳动L的投入每增加1%总产出将增加0.75%。

由于劳动和资本同时扩大λ倍的时候

所以，如果，规模收益递减;如果，规模收益递增;如果，则规模收益不变，此时满足欧拉定理^②。

图4-1　马克思生产函数的等产量曲面(本图用R语言做成^③)

Fig.4-1　Equal output surface of Marx’s production function

参数α和β一般采用最小二乘法估出^[⑨]。柯布和道格拉斯的最初估值是和。

从大西(2002)开始阐述了他对马克思劳动价值论的基本认识，并特别关注了最优资本劳动比率(资本有机构成)问题^[15,16]。然后从大西、山下(2002a)开始，对C-D生产函数作了新的解释，发表了一系列研究成果^[17-25]，之后在大西(2012)中作了一个总结。^[26]

Y表示消费资料总产量，L表示劳动投入量，s表示总劳动中用于消费资料生产的比率，K表示生产手段投入量，A表示全要素生产率。参数α和β分别是资本和劳动的产出弹性产出弹性。于是有

令，表示折旧率，表示劳动生产率，则有

由此他导出了最优资本劳动比率(资本有机构成)为(下式中是时间偏好率):

据此，大西(2012)还进一步导出了最优状态下的劳动投入构成(简单再生产)如下表所示:

表4-1　最优状态下的劳动投入构成(简单再生产)

Table 4-1　Composition of labor input in optimal state(simple reproduction)

第Ⅰ部类	0
第Ⅱ部类

注:译自大西(2012)第118页。

接着，大西(2012)还导出了最优状态下的劳动投入构成(扩大再生产)如下表所示。

表4-2　最优状态下的劳动投入构成(扩大再生产)

Table 4-2　Composition of labor input in optimal state(expanded reproduction)

				总计
第Ⅰ部类	0
第Ⅱ部类
全社会

注:译自大西(2012)第129页。

之后，大西还运用C-D生产函数的分析手法讨论了资本有机构成的提高与相对人口过剩规律、平均利润率下降规律以及先富、后富等问题^[26-29]。

尽管在大西广的分析结果中不乏饶有兴味之处，但是因为他是通过强行重新定义C-D生产函数而建立起的马克思生产函数，令人总有略显牵强的感觉。与此相比，曾尔曼从马克思的价值等式出发尝试去沟通与C-D生产函数的关系，就多了一层理论上必要的衔接手续。曾尔曼通过定义，之后，提出C-D生产函数化之后的马克思的生产函数为^[30]

不过该公式的脉络并不够清晰^[⑩]。不过，从公式(3-3)出发，令，，可得

(4-1)

于是有

(4-2)

这样，我们倒是勉强可把线性的马克思生产函数比较合理地化为C-D型生产函数。不过，如何解释与的经济学含义是一个问题，且放在这里“备案存查”吧。

5　从特殊到一般的生产函数

在上一节我们讨论了马克思生产函数的指数化问题，其间的关联性似乎有些牵强。其实线性的马克思生产函数与C-D生产函数还存在另一种必然联系，为了说明这一问题，需要从“此山中”中跳出来，站在更高的层次上回头俯视。

近年，生产函数从特殊到一般的研究取得了长足的进步。

生产函数的第一次一般化是由于CES(Constant Elasticity of Substitution)函数的出现，该函数最早是由曾经作过Leontief的研究助理的索罗(Robert Merton Solow，1924-)提出来的。索罗(1956)提出了一个两个生产要素的CES生产函数^[31]，然后在1961年被四位经济学家(后来被简称为ACMS)，即阿罗(Kenneth Joseph Arrow，1921-2017)、钱纳里(Hollis Burnley Chenery，1918-1994)、明哈斯(Bagicha Singh Minhas，1922—2005)加上索洛自己所推广^[32]。

两个生产要素的CES生产函数可如下所示:

(5-1)

式中，表示产量，表示要素生产率，表示比例参数(一般)，表示生产要素(资本与劳力)的投入量，表示替代参数，表示替代弹性()，表示生产函数的同质化程度(恒定的规模回报)，s<1(规模收益递减)，v>1(规模报酬递增)。

当时为线性的或者完全替代生产函数，可以证明，当趋向于0时为柯布-道格拉斯生产函数;而趋向于负无穷大时则为Leontief生产函数(即固定投入比例生产函数)。

当，，，且的时候，两个生产要素的CES生产函数可以化为

令，，我们就得到了马克思生产函数。

而当，比例参数，替代参数趋于0，生产函数的同质化程度的时候，两个生产要素的CES生产函数(5-1)趋于C-D生产函数，即有^[33]

在这里我们看到，马克思生产函数和C-D生产函数都可以一般化到CES生产函数(5-1)。可以考虑把马克思生产函数一般化为如下CES生产函数形式:

(5-2)

而Leontief生产函数(固定投入比例生产函数)本来与马克思生产函数就是兼容的，在某种意义下或者在某些方面，可以理解为马克思生产函数的具体化。现在我们看到，Leontief生产函数也属于CES生产函数的特例，这样可以进一步认识两者之间的联系^[11]。

生产函数的第二次一般化是由于VES(Variable Elasticity 0f Substitution)生产函数的出现，根据Constantin Chilarescu(2021)的考证^[34]，该函数最早是由Liu和Hildebrand(1965)提出^[35]，之后有Lu(1967)的贡献^[36]，Sato和Hoffman(1968)^[37]以及 Revankar(1971)^[37]做了进一步的开发。

CES(Constant Elasticity of Substitution)的含义是不变替代弹性，VES生产函数的出发点则在于取消这一假定，VES(Variable Elasticity of Substitution)的含义是可变替代弹性。

在Sato和Hoffman(1968)中，假定，便得到

(5-3)

与前述CES生产函数(5-1)即相比，显然其中的联系主要在于在(5-3)中，，还有需要注意的是，源于前面定义过的。由此可知，当时，则退化为不变替代弹性，从而(5-3)退化为(5-1)，即VES生产函数退化为CES生产函数。

在Revankar(1971)中则进一步假定:，于是得到

(5-4)

式中，，由此可以推出，当时，(5-4)退化为(5-1);当，时，(5-4)退化为C-D型生产函数;当，时，(5-4)退化为C-D型生产函数^[12]。

由于可以理解为资本有机构成，所以可以考虑把马克思生产函数进一步一般化为VES生产函数，即公式(5-4)的形式。这些工作，有待于进一步的开发，本文在这里先提起一个话头，希望能起到抛砖引玉的作用。

利益冲突: 作者声明无利益冲突。

---

---

参考文献(References)

[1] ROBBINS, Lord. Schumpeter on the History of Economic Analysis[M/OL]//The Evolution of Modern Economic Theory: and Other Papers on the History of Economic Thought. London: Palgrave Macmillan UK, 1970: 47-72.
https://doi.org/10.1007/978-1-349-00876-6_2.
[2] BRUE S L. Retrospectives: The Law of Diminishing Re- turns[J]. The Journal of Economic Perspectives, 1993, 7(3): 185-192.
[3] 安妮·罗伯特·雅克·杜尔哥. 杜尔哥和有关文献: 第2 卷[M].
[4] 杜阁著, 南开大学经济系经济学说史教研组译. 关于财富的形成和分配的考察[M/OL]. 北京: 商务印书馆, 1961.
https://ndlsearch.ndl.go.jp/books/R100000002-I022596492.
[5] An Essay on the Co-ordination of the Laws of Distribution[ J].
[6] 編同志社商学編集委員会. 同志社商学=The Doshisha business review[Z/OL]. 同志社大学商学会, 1949.
https://ndlsearch.ndl.go.jp/books/R100000002-I000000016617.
[7] 熊彼特. 《经济发展理论》[M]. 1912.
[8] 阿尔弗雷德·马歇尔. 《经济学原理》: 第六版[M].
[9] 高鸿业. 西方经济学: 第343-345页[M]. 北京: 中国人民大学出版社, 2000.
[10] 马克思、恩格斯. 《马克思恩格斯全集》: 第23卷第238页[M]. 北京: 人民出版社, 1972
[11] 马克思、恩格斯. 《马克思恩格斯全集》: 第25卷第30页[M]. 北京: 人民出版社, 1975.
[12] 马克思、恩格斯. 《马克思恩格斯全集》: 第25卷第242页[M]. 北京: 人民出版社, 1975.
[13] 《马克思恩格斯全集》: 第25卷第158页[M]. 北京: 人民出版社, 1975.
[14] 政治经济学的常识. 菲利普·威克斯蒂德[M]. 1910.
[15] 大西广. 《新教育推荐 经济学》[M]. 2002.
[16] 大西广. 《马克思的经济学》[M]. 2002.
[17] 大西广, 山下裕歩. 重构马克思经济学: 历史唯物论、劳动价值论、剩余价值论[M]. 2002.
[18] 京都大学working paper[N]. No. J-20.
[19] 京都大学working paper[N]. No. J-28.
[20] 大西广, 山下裕歩. 时间偏好率、阶级分裂以及初期资产差距对“马克思·模型的影响: 结果的收入差距和路径的最优化[M]. 2002.
[21] 山下裕歩, 大西广. “马克思模型的各种性质与作为生产要素の劳动的本源性[J]. 经济论丛, 2003, 172(3).
[22] 大西广. 关于市場和资本主义的关系在历史唯物论上的理解[J]. 季刊经济理论, 2005, 42: 1.
[23] 大西广, 金江亮. 马克思主义最优增长理论的目标与挑战[J]. 立命馆经济学, 2008, 56, 5-6.
[24] 大西广, 金江亮. 马克思主义最优增长理论的目标与挑战[J]. 立命馆经济学, 2008, 56, 5-6.
[25] 大西广. 马克思主义最优增长理论的社会人文观[J]. 经济论丛, 2010. , 184, 4.
[26] 大西广. 马克思经济学[M]. 庆应义塾大学出版会, 2012: 133-140.
[27] 山下裕步, 大西广, 茹仙古丽·吾甫尔. 关于马克思最优增长论的解释—最优迂回生产程序的资本主义数学模型[J]. 海派经济学, 2004, 11.
[28] 孙世强, 大西广. 日本马克思学界对社会再生产理论研究的新阐释及启示———基于最优经济增长模型视角[J]. 马克思主义研究, 2014, 8.
[29] 乔晓楠, 何自力. 唯物史观、动态优化与经济增长———兼评马克思主义政治经济学的数学化[J]. 经济研究, 2017, 8.
[30] 曾尔曼. 重建个人所有制的技术进步路径———马克思 生产函数理论导引[J]. 前沿科学, 2010, 4.
[31] SOLOW R M. A Contribution to the Theory of Economic Growth[J/OL]. The Quarterly Journal of Economics, 1956, 70(1): 65-94.
DOI:10.2307/1884513
[32] ARROW K J, CHENERY H B, MINHAS B S, et al. Capital-Labor Substitution and Economic Efficiency[J/OL]. The Review of Economics and Statistics, 1961, 43(3): 225-250.
DOI:10.2307/1927286
[33] 高木尚文. azii: 《成城大学经济研究》第36期[M].
[34] CHILARESCU C. A production function with variable elasticity of substitution greater than one[M]. 2021.
[35] HEADY E O. Hildebrand, George H. , and Ta-Chung Liu, Manufacturing Production Functions in the United States, 1957, An Interindustry and Interstate Comparison of Productivity, Ithaca, New York State School of Ind[J]. American Journal of Agricultural Economics, 1966, 48(1): 144-145.
[36] LU Y. Variable elasticity of substitution production functions, technical change and factor shares [C/ OL]. 1967.
https://api.semanticscholar.org/CorpusID:153133425.
[37] SATO R, HOFFMAN R F. Production Functions with Variable Elasticity of Factor Substitution: Some Analysis and Testing[J/OL]. The Review of Economics and Statistics, 1968, 50(4): 453-460.
https://doi.org/10.2307/1926813.

An Extended Exploration on Marx's Thought of Production Function

ZHANG Zhongren

(The University of Shimane, 2433-2 Nobaracho, Hamada, Shimane 697-0016, Japan)

Abstract: The topics presented in this paper are all new attempts to some extent, and so far, although there is some kind of attempts to reinterpret Marx's economic theory by using the Cobb-Douglas production function, there are few systematic studies of Marxist economics from the point of view of the production function. This paper reveals clear evidence that Marx had the idea of the production function in Capital and emphasizes that there is no such formulation in Capital as the so-called Marxian value equation c+v+m = w , written in letters, but that the formula W =c+v+m , which appears for the first time in Volume III of Capital, belongs to the typical format of a linear production function. From this it can also be recognized that the vertical Leontief production function actually stems from the decomposition of the variable capital part of Marx's production function. In terms of research methodology, this paper, based on a multi-party series of research results obtained from the study of production functions from the special to the general, after clarifying that the basic characteristic of Marx's production function is a linear production function, it achieves generalization by expanding it into the form. of the CES production function, thus clarifying the intrinsic connection between Marx's linear production function and other forms of production functions. The significance of this paper lies mainly in the fact that by exploring and analyzing Marx's idea of the production thought, we can deepen our understanding of Marx's economic theory, especially by further expanding the model of economic growth derived from the reproduction schema, and be conducive to comparative analyses with the economic theories of other schools of thought.  

Keywords: Marx production function, CES production function, VES production function, linear homogeneous production function, Euler's theorem

DOI: 10.48014/jce.20231111002

Citation: ZHANG Zhongren. An extended exploration on Marx's thought of production function[J]. Journal of Chinese Economy, 2024, 3(2): 18-29.