交互式路径随机基因转录模型中 mRNA数量分布的计算
(广州大学数学与信息科学学院, 广州 510006)
摘要: 基因表达是一个随机过程, 表现为等基因细胞群单个细胞中mRNA数量的波动性。这种波动可由mRNA数量分布Pm (t) 来刻画, 其中Pm (t) 是指在t时刻产生m个mRNA分子的概率。对于一个给定的随机基因转录模型, 如何求解对应的Pm (t) 精确表达式一直是该领域的研究热点。在现有工作中, 大多数结果是在稳态情形或者特定的参数区域内来求解Pm (t) , 这影响了我们全面理解不同随机基因调控模式对mRNA数量分布的动力学影响。本论文中, 我们探讨了交互式信号路径随机基因转录模型的Pm (t) 计算, 并给出了其在任意系统参数条件下的精确表达式。交互式信号路径模型被成功应用于阐述可诱导基因应对环境变化下的随机转录数据。这项工作为我们进一步研究基因转录的交互式信号路径调控机制提供动力学理论基础。
关键词: 随机基因转录模型, 化学反应主方程, mRNA 数量分布, 超几何函数
DOI: 10.48014/jcss.20240314001
引用格式: 陈欣欣, 焦锋. 交互式路径随机基因转录模型中mRNA数量分布的计算[J]. 中国统计科学学报, 2024, 2(1): 1-9.
文章类型: 研究性论文
收稿日期: 2024-03-14
接收日期: 2024-03-21
出版日期: 2024-03-28
1 引言
基因转录是一个随机过程，可以通过等基因细胞群中同一基因mRNA水平的波动现象来表现[1-3]。通过使用单分子荧光原位杂交等方法测量单个细胞中mRNA分子的数量，我们可以量化转录波动[4-6]。同时，这种量化提供了详尽的数据，可用于刻画mRNA数量分布的直方图，为近似得出质量函数
和在
时刻时细胞中恰好有
个mRNA分子的概率提供了统计基础[7-9]。同时，从大量实验数据中，我们观察到，在单细胞研究中，大多数mRNA的分布属于以下三种类型:递减分布(图1a)，如哺乳动物细胞中的
启动子[4]，其中随降低;单峰分布(图1b)，如酵母细胞中的管家基因[10]，在
时仅达到一次峰值;双峰分布(图1c)，如小鼠胚胎干细胞中的
基因[11]，其中恰好有两个峰:第一个峰在
处，第二个峰在
时。当直方图和质量函数与随机基因转录中数学框架相结合，提供了将分布数据转换为大量转录调控方案的常规方法[2,4,6,10,12]。
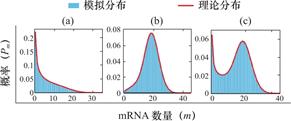
图1 mRNA分布三种类型:(a)递减分布:质量函数Pm随着mRNA分子数量m增大逐渐减少;(b)单峰分布:Pm在m>0处有唯一峰值;(c)双峰分布:Pm有两个峰:一个在m=0处，另一个在m>0处
Fig.1 Three types of mRNA distributions:(a)decreasing distribution:the mass function Pmdecreases gradually as the number m of mRNA molecules increases;(b)single-peak distribution:Pm has a unique peak at m>0;(c)bimodal distribution:Pm has two peaks:one at m=0，and the other at m>0
经典的电报模型是用于描述基因转录随机爆发的标准模型，在几乎所有的活跃的基因组位点里面，mRNA的合成过程中都存在着无法预料的基因激活期和关闭期[1-6]。电报模型表明，基因在基因开启(激活)和关闭(非激活)状态之间随机过渡，且仅在激活状态下合成新的mRNA分子，如下所示:
gene off
gene on
mRNA
Ø(1.1)
该模型由限速步骤以及激活率
、失活率
、生成率
和降解率
决定。
在经典电报模型(1.1)中，对于一群处于稳态的等基因细胞群，我们发现只能生成三种类型的稳态分布[13]:
，即大多数基因关闭时，通常为递减分布;
，即大多数基因开启时，通常为单峰分布;
和
时，即基因的开关状态是平衡的，像这样的保守转录方式通常是双峰分布[1,13,14]。由于动态分布模式和系统动力学参数之间没有简单的对应关系，因此对分布动力学的情况进行探讨是一个不错的角度。例如，当在稳态下呈现单峰分布时，随着时间的推移，单个系统可以呈现所有的衰减、双峰和单峰分布[7,15,16]，正如在大肠杆菌、酵母和哺乳动物细胞中的诱导基因所观察到的那样[16-19]。中间产生的双峰分布表明，细胞在应对环境压力时会进行动态对冲策略[17,20]，其持续时间受到动力学速率[7,15]和基因激活途径的严格调控[9,21]。
经典电报模型默认基因从关闭状态到开启状态是由单一信号通路指导的。然而，一方面，对于在正常条件下生长的细胞，这种默认显然是不合理的。因为它们是通过自发基础通路诱导一大类可诱导基因，将转录水平维持在较低水平[22,23]，同时通过特定的信号通路上调转录水平来应对外部的剧烈变化[17,24]。另一方面，参与干细胞更新、发育和免疫的基因的激活通常也由两种信号途径来进行介导[25-27]，在这些情况下，一个途径中的下游特异性转录因子(TFs)与另一个途径中的其他下游特异性转录因子(TFs)竞争，在其共享的启动子位点结合，以指导中间复合物的形成[17,28]，因此，可以产生两个竞争性的交互式通路来激活靶基因。我们将这两个竞争性的交互式通路整合到基因激活过程中[28,29]，电报模型可以推广为如下模型:
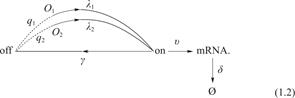
其中基因的转录过程既可以由第一种途径诱导，也可以由第二种途径诱导。在两条路径中，基因激活的持续时间独立且呈指数分布，其中第一条诱导通路诱导强度满足
，第二条通路的诱导强度满足
，他们之间满足
如果基因关闭状态通过第一个途径转化为基因开启状态，我们将其命名为
，否则将其命名为
。那么这其中的选择路径的概率，可以表示为
满足式子
而对于其他的参数，比如基因从开启状态到关闭状态的失活率，mRNA分子的生成率和死亡率，分别由一级动力学速率，和控制，这一点与电报模型相同。
当时间趋于无穷时，处于交互式路径随机基因转录模型中的稳态的质量函数
的具体形式已经被表达出来了[29]，而随后的数值例子表明，与
或
的单一路径相比，在交互式路径中更容易产生双峰分布。这个现象带来了一个问题，即随着时间的发展，交互式路径调控模式是否仍然能保持稳定的双峰分布?然而，当时间有限时，由于模型自带的复杂性，的解析公式一直难以被精确式子表达。目前只有在少数论文中考虑了单一路径的情况，并在一定参数区域下以积分
、无穷级数[15,30]和超几何函数[14,31]的形式表示或相应的生成函数
。我们将在下一节中用简单的数学公式计算出交互式随机基因转录模型中mRNA数量分布的表达式。
2 在交互式路径随机基因转录模型中mRNA数量分布的表达式
我们设
为选择第
条途径，且在时刻存在个mRNA分子的概率，
为基因处于激活状态，且在时刻存在个mRNA分子的概率，那么总概率质量函数是
根据随机过程中求解主方程的一般思路，
的计算可以转化为求解初始时刻无活性基因和零转录分子的化学主方程
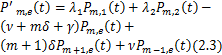
并且
。
下面介绍概率生成函数
概率生成函数将主方程
的初值问题转化为一阶偏微分方程系统
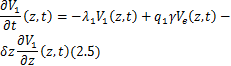
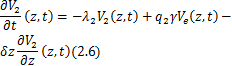
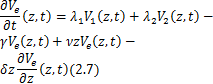
将上述初值问题
的三个解相加，然后应用转换公式求解
其中，
，
。我们用mRNA降解率对系统参数进行无量纲化，得到
且两个实数
和
(
)由下列式子得出
接下来，我们计算所有参数均是正有限的情况下生成函数的一个新的解析式。首先引入广义超几何函数
，定义为:
定理:在交互式随机基因转录模型中，如果所有参数都是正有限的，则生成函数可以用下式表示
其中
，
A(s)=(-1)(-1)
(
+1-，
+
1-;-，1+-;s)×(+1-
，+1-;1-，1+-;s)-
(-1)(-1)(+1-，+
1-;1-，1+-;s)×(+1-
，+1-;-，1+-;s)+
s2a[(-1)×(1+-，1+-
;2-，1+-;s)×(+1-，+
1-;1-，1+-;s)-(-1)(1+
-，1+-;2-，1+-;s)×
(+1-，+1-;1-，1+-;s)]
B(s)=
(+2，+
2;+2，+2;s)×(+1-，+
1-;1-，1+-;s)-(-1)(+
1，+1;+1，+1;s)×(+1-
，+1-;-，1+-;s)+as[(1+
-，1+-;2-，1+-;s)×
(+1，+1;+1，+1;s)s+
(-1)(，;，;s)×(+
1-，+1-;1-，1+-;s)]
C(s)=
(+2，+
2;+2，+2;s)×(+1-，+1-
;1-，1+-;s)+(-1)(+
1，+1;+1，+1;s)×(+1-
，+1-;-，1+-;s)+
(，;，;s)×
(+1-，+1-;1-，1+-
;s)-(1+-，1+-;2-，1+
-;s)×(+1，+1;+1，+1;s)s]
A、B、C分别由四个广义超几何函数组成。
证明:设z0为参数，且
ui(t)=Vi(z0eδt，t)i=1，2，e
u(t)=u1(t)+u2(t)+u3(t)
式(2.5)~(2.7)可转化为常微分方程
u'1(t)=-λ1u1(t)+q1γue(t)，
u'2(t)=-λ2u2(t)+q2γue(t)，(2.9)
u'e(t)=λ1u1(t)+λ2u2(t)-γue(t)+νz0eδtue(t)，(2.10)
u1(0)=q1，u2(0)=q2，ue(0)=0，(2.11)
为了进一步变换系统，我们定义
ωi(x)=ui(t)i=1，2，e ω(x)=u(t)，x=
eδt
得到u'i(t)=δxω'i(x)。则式子(2.9)-(2.11)可转化为
xω'1(x)=-ω1(x)+q1
ωe(x)，
xω'2(x)=-ω2(x)+q2ωe(x)
xω'e(x)=ω1(x)+ω2(x)-ωe(x)+xωe(x)，
ω1()=q1，ω2()=q2，ωe()=0
定义a，b，c和d为实常数，f=f(x)为关于x的光滑函数，我们给出一个线性算子
(f)=x2f‴(x)+x(1-x+c+d)f″(x)+
(cd-x(a+b+1))f'(x)-abf(x)
w(x)是下面初值问题的唯一解[15]
(ω)=0，ω()=1，ω'()=0，
ω″()=(q1+q2)/
由于(ω)=0是广义超几何函数，如果-≠1，2，…，那么存在关于(ω)=0的三个独立的特解，分别为
ω1(t)=(，;，;x)(2.12)
ω2(t)=
(1+-，1+-;
2-，1+-;x) (2.13)
ω3(t)=
(1+-，1+-;
2-，1+-;x) (2.14)
因此，我们推导出(ω)=0的一般解为
ω(x)=Aω1(x)+Bω2(x)+Cω3(x)(2.15)
其中，A、B和C是待定常数。将初值条件
ω()=1，ω'()=0，ω″()=(q1+q2)/
z0
代入式中得到如下方程组
Aω1()+Bω2()+Cω3()=1，(2.16)
Aω'1()+Bω'2()+Cω'3()=0，(2.17)
Aω″1()+Bω″2()+Cω″3()=a(2.18)
为了求解上述方程组，我们将式子(2.18)乘-ω3()/ω″3()，然后再加上式子(2.16)，得到
A[ω1()ω″3()-ω″1()ω3()]+
B[ω2()ω″3()-ω″2()ω3()]
=ω″3()-aω'3() (2.19)
同样地，将式子(2.18)乘-ω'3()/ω″3()，然后再加上式子(2.17)，得到
A[ω'1()ω″3()-ω″1()ω'3()]+
B[ω'2()ω″3()-ω″2()ω'3()]
=-aω'3() (2.20)
通过简单的计算求解式(2.19)和式(2.20)，我们得到
A=
(2.21)
B=
(2.22)
其中
(s)表示如下
(s)=ω1(s)[ω'2(s)ω″3(s)-ω″2(s)ω'3(s)]-
ω'1(s)[ω2(s)ω″3(s)-ω″2(s)ω3(s)]+
ω″1(s)[ω2(s)ω'3(s)-ω'2(s)ω3(s)]
(2.23)
将式(2.21)和式(2.22)代入式(2.18)得到
C=
(2.24)
注意到广义超几何函数的微分理论
=
(x1+k，x2+k;
y1+k，y2+k;x)，k=0，1，… (2.25)
以及
=
(x1，x2;
y1-k，y2;x)，k=0，1，… (2.26)
应用(2.12)~(2.14)和(2.25)，(2.26)，我们有
ω'1(s)=
(+1，+1;+1，+1;s)，(2.27)
ω″1(s)=
(+2，+2;+2，+2;s)， (2.28)
ω'2(s)=
(-+1，-+1;
1-，1+-;s)， (2.29)
ω″2(s)=-
(-+1，-+1;
-，1+-;s)， (2.30)
ω'3(s)=
(-+1，-+1;
1-，1+-;s)， (3.31)
ω″3(s)=-
(-+1，-+1;
-，1+-;s) (3.32)
我们要求
(s)=(-)(-1)(-1)es
为了证明上式，我们注意到ω1，ω2和ω3是三阶常微分方程(ω)=0的独立解。因此，对于许多给定的实数s0，(s)取如下形式
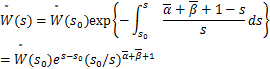
由于s0是任意的，所以我们选择s0=0。注意到(x1，x2;y1，y2;0)=1。我们现在可以把(2.21)~(2.24)代入(2.15)，得到
ω(x)=
[ω'2()ω″3()-
ω″2()ω'3()+a(ω2()ω'3()-
ω'2()ω3())]+
[ω'3()ω″1()-
ω″3()ω'1()+a(ω3()ω'1()-
ω'3()ω1())]+
[ω'1()ω″2()-
ω″1()ω'2()+a(ω1()ω'2()-
ω'1()ω2())]
将(2.27)~(2.32)代入ω(x)得到
ω(x)=
ω1(x)+
ω2(x)+
ω3(x)
A(s)=(-1)(-1)(+1-，+1-;
-，1+-;s)×(+1-，+1-
;1-，1+-;s)-(-1)(-
1)(+1-，+1-;1-，1+
-;s)×(+1-，+1-
;-，1+-;s)+s2a[(-1)×
(1+-，1+-;2-，1+-
;s)×(+1-，+1-;1-，1+
-;s)-(-1)(1+-，1+-
;2-，1+-;s)×(+1-，+
1-;1-，1+-;s)]
B(s)=(+2，+
2;+2，+2;s)×(+1-，+
1-;1-，1+-;s)-(-1)(+
1，+1;+1，+1;s)×(+1-
，+1-;-，1+-;s)+as[(1+
-，1+-;2-，1+-;s)×
(+1，+1;+1，+1;s)s+
(-1)(，;，;s)×
(+1-，+1-;1-，1+-;s)]
C(s)=(+2，+
2;+2，+2;s)×(+1-，+
1-;1-，1+-;s)+(-1)(+
1，+1;+1，+1;s)×(+1-
，+1-;-，1+-;s)+
(，;，;s)×
(+1-，+1-;1-，1+-
;s)-(1+-，1+-;2-，1+
-;s)×(+1，+1;+1，+1;s)s]
通过将x替换成z，将z0替换成ze-δt，我们将ω(x)转换为V(z，t)，从而完成了定理的证明。
3 总结
在本文中，我们受到以往方法的启发，在交互式路径随机基因转录模型中，在参数都是正的且有限的情况下计算出了生成函数的精确表达式。该方法可以在一般参数条件下进一步发展，将参数范围具体化，从而简化生成函数，进而可以逆推出质量函数，进行更多的分析。交互式信号路径模型被成功用来阐述细菌、酵母和哺乳动物细胞中可诱导基因应对环境变化时的随机转录数据
。这项工作为我们进一步研究基因转录的交互式信号路径调控机制提供动力学理论基础。
利益冲突: 作者声明无利益冲突。
[①] *通讯作者 Corresponding author:焦锋，jiaof@gzhu.edu.cn
收稿日期:2024-03-14; 录用日期:2024-03-21; 发表日期:2024-03-28
参考文献(References)
[1] Munsky B, Neuert G, van Oudenaarden A. Using gene expression noise to understand gene regulation[J]. Science, 2012, 336: 183-187.
https://doi.org/10.1126/science.1216379
[2] Sanchez A, Golding I. Genetic determinants and cellular constraints in noisy gene expression[J]. Science, 2013, 342: 1188-1193.
https://doi.org/10.1126/science.1242975
[3] Larsson A J M, et al. Genomic encoding of transcriptional burst kinetics[J]. Nature, 2019, 565: 251-254.
https://doi.org/10.1038/s41586-018-0836-1
[4] Raj A, Peskin C S, Tranchina D, et al. Stochastic mRNA synthesis in mammalian cells[J]. PLoS Biol, 2006, 4: e309.
https://doi.org/10.1038/s41586-018-0836-1
[5] Halpern K B, et al. Bursty gene expression in the intact mammalian liver[J]. Cell, 2015, 58: 147-156.
https://doi.org/10.1016/j.molcel.2015.01.027
[6] Dey S S, Foley J E, Limsirichai P, et al. Orthogonal control of expression mean and variance by epigenetic features at different genomic loci[J]. Mol Syst Biol, 2015, 11: 806.
https://doi.org/10.15252/msb.20145704
[7] Jiao F, Tang M, Yu J. Distribution profiles and their dynamic transition in stochastic gene transcription[J]. J. Differential Equations, 2013, 254: 3307-3328.
https://doi.org/10.1016/j.jde.2013.01.019
[8] Munsky B, Fox Z, Neuert G. Integrating single-molecule experiments and discrete stochastic models to understand heterogeneous gene transcription dynamics[J]. Methods, 2015, 85: 12-21.
https://doi.org/10.1016/j.ymeth.2015.06.009
[9] Chen J, Grima R. Dynamical phase diagram of an autoregulating gene in fast switching conditions[J]. J. Chem. Phys, 2020, 152: 174110.
https://doi.org/10.1063/5.0007221
[10] Zenklusen D, Larson D R, Singer R H. Single-RNA counting reveals alternative modes of gene expression in yeast[J]. Nat. Struct. Mol. Biol, 2008, 15: 1263-1271.
https://doi.org/10.1038/nsmb.1514
[11] Kalmar T, et al. Regulated fluctuations in Nanog expression mediate cell fate decisions in embryonic stem cells[J]. PLoS Biol, 2009, 7: e1000149.
https://doi.org/10.1371/journal.pbio.1000149
[12] Senecal A, et al. Transcription factors modulate c-Fos transcriptional bursts[J]. Cell Rep, 2014, 8: 75-83.
https://doi.org/10.1016/j.celrep.2014.05.053
[13] Jiao F, Sun Q, Tang M, et al. Distribution modes and their corresponding parameter regions in stochastic gene transcription[J]. SIAM J. Appl. Math, 2015, 75: 2396-2420.
https://doi.org/10.1137/151005567
[14] Iyer-Biswas S, Hayot F, Jayaprakash C. Stochasticity of gene products from transcriptional pulsing[J]. Phys. Rev. E, 2009, 79: 031911.
https://doi.org/10.1103/PhysRevE.79.031911
[15] Jiao F, Ren J, Yu J. Analytical formula and dynamic profile of mRNA distribution[J]. Discrete Contin. Dyn. Syst. B, 2020, 25: 241-257.
https://doi.org/10.3934/dcdsb.2019180
[16] Golding I, Paulsson J, Zawilski S M, et al. Real-time kinetics of gene activity in individual bacteria[J]. Cell, 2005, 123: 1025-1036.
DOI:
https://doi.org/10.1016/j.cell.2005.09.031
[17] Pelet S, et al. Transient activation of the HOG MAPK pathway regulates bimodal Gene expression[J]. Science, 2011, 332: 732-735.
https://doi.org/10.1126/science.1198851
[18] Neuert G, et al. Systematic identification of signal-activated stochastic gene regulation[J]. Science, 2013, 339: 584-587.
https://doi.org/10.1126/science.1231456
[19] Fiering S, et al. Single cell assay of a transcription factor reveals a threshold in transcription activated by signals emanating from the T-cell antigen receptor[J]. Genes Dev, 1990, 4: 1823-1834.
https://doi.org/10.1101/gad.4.10.1823
[20] Larson D R. What do expression dynamics tell us about the mechanism of transcription[J]. Curr. Opin. Genet. Dev, 2011, 21: 1-9.
https://doi.org/10.1016/j.gde.2011.07.010
[21] Zhu C, Han G, Jiao F. Dynamical regulation of mRNA distribution by cross-talking signaling pathways[J]. Complexity, 2020, 20: 6402703.
https://doi.org/10.1155/2020/6402703
[22] Macia J, Regot S, Peeters T, et al. Dynamic signaling in the Hog1 MAPK pathway relies on high basal signal transduction[J]. Sci. Signal, 2009, 2, ra13.
https://doi.org/10.1126/scisignal.2000056
[23] Jordan A, Defechereux P, Verdin E. The site of HIV-1 integration in the human genome determines basal transcriptional activity and response to Tat transactivation[J]. EMBO J, 2001, 20: 1726-1738.
https://doi.org/10.1093/emboj/20.7.1726
[24] Nadal E, Ammerer G, Posas F. Controlling gene expression in response to stress[J]. Nat. Rev. Genet, 2011, 12: 833-845.
https://doi.org/10.1038/nrg3055
[25] Aguirre A, Rubio M E, Gallo V. Notch and EGFR pathway interaction regulates neural stem cell number and self-renewal[J]. Nature, 2010, 467: 323-327.
https://doi.org/10.1038/nature09347
[26] Yoo A S, Bais C, Greenwald I. Crosstalk between the EGFR and LIN-12/Notch pathways in C. elegans vulval development[J]. Science, 2004, 303: 663-666.
https://doi.org/10.1126/science.1091639
[27] Tanji T, Hu X, Weber A N R, et al. Toll and IMD pathways synergistically activate an innate immune response in Drosophila melanogaster[J]. Mol. Cell. Biol, 2007, 27: 4578-4588.
https://doi.org/10.1128/MCB.01814-06
[28] Yu J, Tang M, Sun Q. The nonlinear dynamics and fluctuations of mRNA levels in cross-talking pathway acti- vated transcription[J]. J. Theor. Biol, 2014, 363: 223-234.
https://doi.org/10.1016/j.jtbi.2014.08.024
[29] Jiao F, Sun Q, Lin G, et al. Distribution profiles in gene transcription activated by the cross-talking pathway. Discrete Contin[J]. Dyn. Syst. B, 2019, 24: 2799-2810.
https://doi.org/10.3934/dcdsb.2018275
[30] Tabaka M, Holyst R. Binary and graded evolution in time in a simple model of gene induction[J]. Phys. Rev. E, 2010, 82: 052902.
https://doi.org/10.1103/PhysRevE.82.052902
[31] Shahrezaei V, Swain P S. Analytical distributions for stochastic gene expression[J]. Proc. Natl. Acad. Sci, 2009, 105: 17256-17261.
https://doi.org/10.1073/pnas.0803850105
[32] Zhou T, Zhang J. Analytical results for a multistategene model[J]. SIAM J Appl Math, 2012, 72: 789-818.
https://doi.org/:10.1137/110852887
[33] Sun Q, Cai Z, Zhu C. A novel dynamical regulation ofmRNA distribution by cross-talking pathways[J]. Mathematics, 2022, 10: 1515.
https://doi.org/10.3390/math10091515
[34] Jiao F, Zhu C. Regulation of gene activation by competitivecross talking pathways[J]. Biophys. J, 2020, 119: 1204-1214.
DOI:10.1016/j.bpj.2020.08.011
[35] Chen L, Lin G, Jiao F. Using average transcription levelto understand the regulation of stochastic gene activation[J]. R. Soc. Open Sci, 2022, 9: 211757.
https://doi.org/10.1098/rsos.211757
Computation of mRNA Number Distributions in Interactive Pathway Stochastic Gene Transcription Model
(School of Mathematics and Information Science, Guangzhou University, Guangzhou 510006, China)
Abstract: Gene expression is a stochastic process characterized by fluctuations in the amount of mRNA in individual cells of an isogenic cell population. The fluctuation can be characterized by the mRNA number distribution Pm (t) , which denotes the probability of producing m copies of mRNA molecules in one cell at time t. For a given stochastic gene transcription model, how to solve the corresponding Pm (t) exact expression has been a hot research topic in this field. In the existing work, most of the results are solved for Pm (t) in the steady state case or in a specific parameter region, which affects us to fully understand the kinetic effects of different stochastic gene regulation patterns on the distribution of mRNA quantities. In this thesis, we explore the computation of Pm (t) for the cross-talk pathway model and give its exact expression under arbitrary system parameter conditions. The interactive signaling pathway model is successfully applied to elaborate stochastic transcription data of inducible genes in response to environmental changes. This work provides a kinetic theoretical basis for us to further investigate the interactive signaling pathway regulatory mechanism of gene transcription.
Keywords: Stochastic gene transcription model, chemical response master equation, quantitative distribution of mRNA, hypergeometric function
DOI: 10.48014/jcss.20240314001
Citation: CHEN Xinxin, JIAO Feng. Computation of mRNA number distributions in interactive pathway stochastic gene transcription model[J]. Journal of Chinese Statistical Sciences, 2024, 2(1): 1-9.