LncRNA 顺式与反式调控基因表达的差异分析

欧阳建志, 肖嘉怡, 陈祝彬, 廖萧雨, 黄丽芳^*

(广东财经大学统计与数学学院, 广州 510320)

摘要: 研究表明长链非编码RNA (lncRNA) 在多个层面上参与重要生命过程的调控。然而迄今为止, lncRNA调控基因表达的机制复杂性及其生物学功能尚未完全阐明。本论文主要针对lncRNA通过顺式和反式两种方式调控基因表达的差异及其动态行为开展研究: 一、基于化学主方程建立lncRNA功能作用的数学模型并验证明了SSA和FSP算法的准确性; 二、利用SSA和FSP算法分析lncRNA分布及转录爆发对基因表达的影响。本文结合动力系统理论和随机模拟方法, 首先构建基于实验结果的lncRNA调控机制模型; 然后通过计算模型的一些关键指标 (如mRNA的概率分布、均值和噪声等) , 分析lncRNA在顺式与反式调控中表现出的动态特性。研究表明原始模型下的反式调控的mRNA表达量更高且噪声更低, 而顺式调控对快速局部响应更加敏感, 还研究了lncRNA生成分布对mRNA表达的动态特性的影响, 发现不同分布形式显著影响调控模式的稳定性和表达效率。同时加入转录爆发后, 相比反式调控, 顺式调控mRNA的表达平均量更高且噪声更低。本研究为全面理解lncRNA的调控机制及其在基因表达中的功能特性提供了理论支持, 为探索lncRNA调控机制提供了新视角。

关键词: lncRNA, 顺式调控, 反式调控, 转录爆发

DOI: 10.48014/jcss.20250125001

引用格式: 欧阳建志, 肖嘉怡, 陈祝彬, 等. LncRNA顺式与反式调控基因表达的差异分析[J]. 中国统计科学学报, 2025, 3(1): 26-38.

文章类型: 研究性论文

收稿日期: 2025-01-25

接收日期: 2025-02-10

出版日期: 2025-03-28

1　引言

长链非编码RNA(long non-coding RNA，lncRNA)是近年来基因组学与分子生物学领域的研究热点，主要指长度超过200核苷酸且不编码蛋白质的RNA分子^[1,2]。研究表明尽管lncRNA不直接编码蛋白质，它们通过多种机制在基因表达调控、染色质重塑、细胞分化及其他生物学过程中发挥了重要作用，这些机制包括与转录因子和染色质修饰复合物的结合、参与RNA加工和翻译调控，以及通过分子间相互作用充当细胞信号网络中的重要节点^[3-8]。

lncRNA的作用机制可大致分为两类:顺式调控和反式调控^[9,10]。顺式调控指lncRNA通过直接作用于基因组附近的靶点(如增强子区域)来调控邻近基因的表达。典型案例包括XIST，其通过染色质修饰使X染色体沉默^[2];而反式调控涉及lncRNA远程作用于其他基因，通过与蛋白质、RNA或DNA相互作用形成复杂的调控网络，例如HOTAIR通过染色质重塑实现基因网络的远程调控^[11]。

尽管近年来实验研究揭示了许多lncRNA的生物功能，但其在基因调控网络中的作用依然充满复杂性和挑战性。一方面，lncRNA具有高度的组织特异性和时间特异性，这使得实验研究难以全面捕捉其动态行为;另一方面，lncRNA在细胞内的低拷贝数和随机表达模式显著增加了研究难度，传统的实验方法难以定量刻画lncRNA的动态特性，数学建模为解析lncRNA调控机制提供了新的途径，通过理论建模和数值分析，可以定量描述lncRNA在基因表达调控中的随机特性，为研究其功能提供定量化视角^[12-13]。例如通过化学主方程和随机模拟方法，可以模拟分子间的相互作用，揭示转录和翻译过程中的动态特性，结合单细胞测序和高通量数据，建模分析能够捕捉生物系统的异质性和多样性，从而为探索lncRNA调控网络提供更深层次的洞察^[14]。

基于上述背景，本文旨在采用化学主方程构建lncRNA调控的数学模型，结合Gillespie随机模拟算法(SSA)和有限状态投影法(FSP)研究lncRNA的顺式与反式调控机制，为了进一步揭示lncRNA动态调控中的关键特性，还分析了lncRNA转录爆发行为对基因表达的影响。这些研究不仅深化了对lncRNA调控网络的理解，还为生物学实验设计和高通量数据的理论分析提供了定量化工具。

2　方法

化学主方程(Chemical Master Equation，CME)是描述离散随机系统的核心工具，用于刻画系统中不同状态随时间的概率变化。对于基因调控网络，CME能够精确描述分子生成、降解以及基因状态转换等随机过程。化学主方程的核心思想基于以下假设:(1)系统的状态变化仅依赖当前状态，与过去的状态无关;(2)分子数量是离散变量;(3)分子生成、降解和状态转换是随机事件，事件发生的时间间隔服从指数分布。

如图1，为了定量描述lncRNA的顺式和反式调控机制，基于化学主方程构建了一个动力学模型，将基因状态和分子数量变化抽象为随机过程。模型假设基因具有三种状态:OFF1、OFF2和ON，分别表示基因处于初始关闭状态、准备激活状态和表达激活状态。两个关键分子，mRNA和lncRNA，分别是基因表达的产物和调控因子，其生成与降解的动态特性在模型中被显式表征。

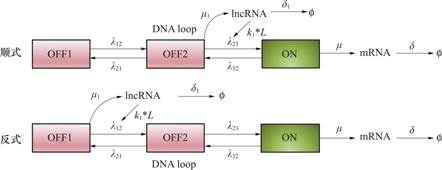
图1　顺式和反式调控图

Fig.1　Cis and Trans-Regulation Diagram

将基因的三种状态分别记为01，02和1状态，p₀₁(m，L，t)，p₀₂(m，L，t)和p₁(m，L，t)分别表示系统在t时刻以及01，02和1状态下有m个mRNA分子、L个lncRNA分子的概率。化学主方程的基本形式为:

=流入速率-流出速率(1)

依据上述在顺式调控中，lncRNA在DNA成环之后通过直接作用调控基因从OFF2切换到ON，速率为k₁·L，以基因在02状态的顺式调控为例，流入方面:基因从01状态切换至02状态的速率为λ₁₂，从1状态切换到02状态速率为λ₃₂;流出方面:基因从02状态切换至01状态速率为λ₂₁，从02状态切换至1状态速率为k₁·L，再结合02状态基因自身的反应，可以得到02状态时物质的化学主方程为:

=-(k₁L+λ₂₁)p₀₂(m，L，t)+λ₃₂p₁(m，L，t)+λ₁₂p₀₁(m，L，t)+δ[(m+1)p₀₂(m+1，L，t)-mp₀₂(m，L，t)]+μ₁[p₀₂(m，L-1，t)-p₀₂(m，L，t)]+δ₁[(L+1)p₀₂(m，L+1，t)-Lp₀₂(m，L，t)](2)

同理可以得到基因在01状态和1状态时的化学主方程:

=λ₂₁p₀₂(m，L，t)-λ₁₂p₀₁(m，L，t)+δ[(m+1)p₀₁(m+1，L，t)-mp₀₁(m，L，t)]+δ₁[(L+1)p₀₁(m，L+1，t)-Lp₀₁(m，L，t)](3)

=k₁Lp₀₂(m，L，t)-λ₃₂p₁(m，L，t)+μ[p₁(m-1，L，t)-p₁(m，L，t)]+δ[(m+1)p₁(m+1，L，t)-mp₁(m，L，t)]+δ₁[(L+1)p₁(m，L+1，t)-Lp₁(m，L，t)](4)

反式调控时化学主方程的形式类似，只不过这时候lncRNA调控发生在DNA成环之前。在建立方程之后对方程的流入和流出概率进行计算，发现系统的流入和流出是平衡的，符合该系统描述化学反应的特点。

2.1　随机模拟算法

Gillespie随机模拟算法(Gillespie Stochastic Simulation Algorithm，SSA)是一种用于描述化学反应网络中分子动态行为的随机算法，与常微分方程假设分子数连续并忽略随机波动不同，SSA明确考虑分子数的离散性以及反应发生时间的随机性，使其成为研究小分子数系统动态特性的核心工具^[15-16]。本文系统的状态通过以下三部分描述:①分子数，包含系统中每种物种的具体分子数量;②反应速率，描述各化学反应发生的可能性，速率取决于系统当前状态;③随机性，假设每次反应的发生时间间隔服从指数分布，系统状态随时间的演化是随机的。

SSA的关键步骤如下:

(1)初始化

定义系统的初始状态，包括分子数反应速率常数，以及模拟的总时间T_max。

(2)计算反应速率

根据当前的状态，计算每种反应的速率a_j，并得到总速率a₀:

a₀=a_j(5)

其中，a_j是第j个反应的速率，通常取决于反应物的数量和速率常数。

(3)随机采样间隔时间

使用指数分布随机生成下一个反应发生的时间间隔:

Δt=(6)

其中，r₁是[0，1]区间的均匀分布的随机数。

(4)选择发生的反应

根据每种反应的速率占总速率的比例，随机选择发生的具体反应:

选择发生的反应j应该满足:

a_k<r₂·a₀£a_k(7)

其中，r₂是另一个[0，1]区间的均匀分布随机数。

(5)更新系统状态

根据选定的反应更新系统状态(分子数或基因状态)，同时更新当前时间t。

(6)迭代

重复步骤2到步骤5，直到达到模拟时间T_max或满足其他终止条件。

在使用SSA求解微分方程时，需确定顺式和反式调控的反应数量以及每个反应发生时基因所在的状态，反应物和生成物的数量变化，下表0表示基因不处于该状态，1表示基因处于该状态。

表1　顺式调控时各个反应状态和物质变化情况

Table 1　Reaction states and material changes under Cis-Regulation

反应	OFF1	OFF2	ON	mRNA	lncRNA	速率
1	0	1	0	不变	不变	λ12
2	1	0	0	不变	不变	λ21
3	0	0	1	不变	不变	k1·L
4	0	1	0	不变	不变	λ32
5	0	0	1	增加1	不变	μ
6	不变	不变	不变	减少1	不变	δ
7	0	1	0	不变	增加1	μ1
8	不变	不变	不变	不变	减少1	δ1

表2　反式调控时各个反应状态和物质变化情况

Table 2　Reaction states and material changes under Trans-Regulation

反应	OFF1	OFF2	ON	mRNA	lncRNA	速率
1	0	1	0	不变	不变	k1·L
2	1	0	0	不变	不变	λ21
3	0	0	1	不变	不变	λ23
4	0	1	0	不变	不变	λ32
5	0	0	1	增加1	不变	μ
6	不变	不变	不变	减少1	不变	δ
7	1	0	0	不变	增加1	μ1
8	不变	不变	不变	不变	减少1	δ1

根据上面表格信息，编写顺式调控和反式调控SSA算法代码，基于SSA算法捕捉了小分子数系统的随机性，通过指数分布计算时间间隔并基于反应速率随机选择反应类型，模拟的结果可用于分析基因调控网络的随机特性，从而得到mRNA表达的概率密度分布。

2.2　有限状态投影算法

化学主方程(CME)是描述生化反应系统随机动态的核心工具，但由于其状态空间通常是无限的或非常高维，直接求解CME在计算上非常困难，特别是在基因表达调控中，mRNA和lncRNA的分子数量可能在广泛范围内波动，基因状态的切换进一步增加了系统的复杂性，有限状态投影法(FSP)通过截断无限状态空间至有限子空间，提供了高效且可控误差的近似求解方法^[17]。

FSP算法的核心思想是将化学主方程的无限状态空间S投影到一个有限状态子空间S_F，在有限状态子空间内求解概率分布，并估计被截断状态的概率质量，以控制误差。这种方法在保证计算效率的同时，严格控制了计算精度，是处理高维生化反应系统的有效工具，其原理如下:

(1)化学主方程形式化

化学主方程描述了系统在时间t处于某一个状态x的概率变化:

=
[W(x|x')P(x'，t)-W(x'|x)P(x，t)](8)

其中:x表示系统状态，包含基因状态和分子数量;W(x|x')表示从状态x'转移到状态x的速率;S表示所有的状态空间。

(2)状态空间截断

将无限状态空间S限制到一个有限子空间S_F，假设状态x∈S_F，则可以在有限空间内定义化学主方程的矩阵形式:

=Q_FP_F(t)(9)

其中:P_F(t)表示有限空间内的概率向量，Q_F表示状态转移速率矩阵，仅定义在S_F上。

(3)误差控制

被截断的概率质量可以通过以下方法估计:

ε=1-P(x，t)(10)

如果ε超过预设的容忍阈值，则扩展子空间S_F，直到满足精度要求。

3　不同算法结果验证

为了验证SSA和FSP这两种完全不同原理的算法捕捉小分子系统动态特性的准确性，固定δ=1，δ₁=1，k₁=1，μ=20，μ₁=5，随机取两组λ₁₂，λ₂₁，λ₂₃，λ₃₂的值，一般情况下t>10000时系统可到达稳定，为了取得更好的拟合效果，模拟时间取t=1000000，计算上节描述的四个指标(稳态的均值、方差、噪声、Fano因子)的结果，并绘制两种不同算法下的顺式调控和反式调控的mRNA概率分布来进行比较。

取第一组参数λ₁₂=0.5，λ₂₁=0.8，λ₂₃=1.2，λ₃₂=2.7，绘制的mRNA稳态概率分布图如图2所示。

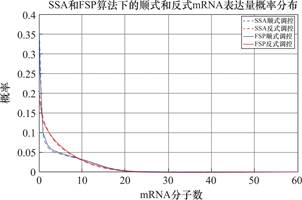
图2　第一组参数绘图结果

Fig.2　Results of the first group of parameters plot

第一组参数计算结果如表3所示。

表3　第一组参数计算结果

Table 3　Calculation results of the first group of parameters

模型	均值	方差	噪声	Fano因子
SSA顺式调控	4.41	27.26	1.40	6.19
FSP顺式调控	4.57	27.18	1.30	5.95
SSA反式调控	4.48	21.18	1.06	4.73
FSP反式调控	4.68	21.47	0.98	4.59

取第二组参数λ₁₂=2，λ₂₁=1.8，λ₂₃=0.7，λ₃₂=0.5，绘制的mRNA概率分布如图3所示。

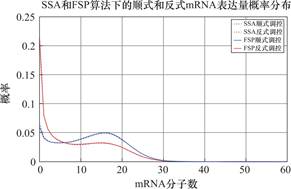
图3　第二组参数绘图结果

Fig.3　Results of the second group of parameters plot

第二组参数计算结果如表4所示。

表4　第二组参数计算结果

Table 4　Calculation results of the second group of parameters

模型	均值	方差	噪声	Fano因子
SSA顺式调控	12.06	55.55	0.38	4.60
FSP顺式调控	12.17	54.61	0.37	4.49
SSA反式调控	8.45	61.86	0.87	7.32
FSP反式调控	8.54	66.61	0.85	7.22

对两种原理完全不同算法的结果，发现两种算法的计算结果非常接近，这证明了本文设计的两种算法计算结果的准确性，为进一步研究lncRNA调控基因表达网络提供了一种可信的计算方法。

4　结果分析

稳定的mRNA平均表达量、噪声和Fano因子都是评估基因表达调控效率的关键指标。在顺式调控机制中，lncRNA通常通过增强子作用于邻近基因，通过调节基因转录启动子区域，促使基因从OFF状态转变为ON状态。反式调控中lncRNA并不直接作用于目标基因的启动子，而是通过与远离基因的调控因子或其他RNA分子相互作用，改变基因表达的调控网络，lncRNA在此过程中的作用更多的是间接的。因此可以通过改变lncRNA的生成速率，计算顺式和反式调控模型中稳态的mRNA平均表达量，确定模型中顺式和反式模型的表达差异。

4.1　顺式和反式调控调控基因表达的比较

一般情况下，基因大部分时间处于OFF状态，从OFF状态切换至ON状态的速率λ₁₂，λ₂₃一般小于从ON状态切换至OFF状态的λ₂₁，λ₃₂的速度。基于以上原则，为比较顺式调控和反式调控下mRNA表达量的大小，令δ=1，δ₁=1，k₁=1，μ=20，μ₁=5，然后随机在以下区间内取1000组值:λ₁₂∈[0.1，0.5]，λ₂₁∈[1，3]，λ₃₂∈[1，3]，λ₂₃=λ₁₂，若顺式平均值大于反式平均值则记为1，否则记为2，随机取点的部分结果如表5所示。

将以上所有数据结果以散点图和箱线图形式表示，结果如图4所示。

表5　初始模型随机取点部分结果

Table 5　Partial results of initial model with randomly selected points

λ21	λ32	λ23	顺式均值	反式均值	顺式噪声	反式噪声	顺式Fano	反式Fano	比较结果
2.86	1.82	0.35	1.30	6.93	9.04	4.31	1.08	4.67	2
1.48	1.69	0.14	1.34	7.54	10.08	7.71	0.64	4.94	2
1.99	2.77	0.18	0.78	10.64	8.33	8.07	0.51	4.13	2
1.44	1.28	0.14	1.73	6.36	11.01	6.59	0.84	5.53	2
2.52	2.90	0.48	1.40	5.17	7.24	6.74	0.62	4.16	2
2.17	1.72	0.30	1.64	5.67	9.33	5.52	0.89	4.91	2
1.16	1.69	0.44	4.22	1.84	7.77	9.30	0.51	4.75	2
2.14	2.72	0.32	1.19	6.55	7.82	7.46	0.56	4.21	2
1.99	1.30	0.23	1.82	5.74	10.43	4.89	1.10	5.40	2

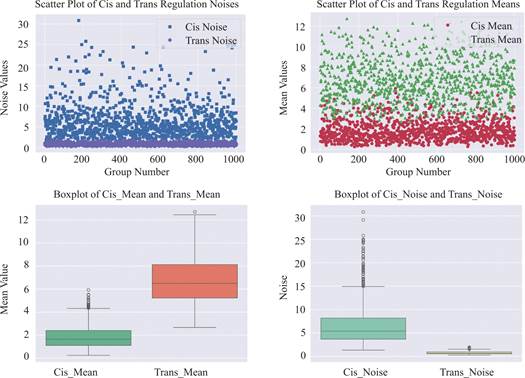
图4　初始模型结果散点图和箱线图

Fig.4　Scatter plot and box plot of initial model results

在该模型下的1000组结果中，同一组参数下，反式调控的mRAN平均值表达量始终高于顺式调控，反式调控的噪声更低，Fano因子也更小，表明反式调控相比顺式调控在基因表达中的随机性更低调控更加稳定。这可能是因为在反式调控模型中，lncRNA的远程作用能够通过复杂的调控网络显著提高基因激活效率，使得平均mRNA表达量高于顺式调控，而顺式调控主要依赖于局部增强子的直接作用，其调控范围和效率相对受限。因此顺式调控可能更适合快速响应的局部基因表达，反式调控的调节可能适用于维持基因网络的长期稳定性。

此外分析数据结果表明，在顺式调控中mRNA的平均表达量与k₁·L正相关，λ₂₁和λ₃₂会影响mRNA表达稳定性，但对表达量的直接影响较弱。在反式调控中mRNA的平均表达量同样与k₁·L正相关，但由于反式调控涉及到远程作用，其噪声较小表达更加稳定。

4.2　lncRNA的不同分布调控

lncRNA作为基因表达调控网络中的重要分子，其作用机制在时空维度上具有高度动态性。近年来的研究表明，lncRNA的表达调控不仅受限于其生成和降解的分子机制，还与其时空分布特性密切相关。尤其是在复杂的生物系统中，lncRNA的表达状态通常呈现出高度多样化的分布形式，这种分布特性可能显著影响其对目标基因的调控效率。

4.2.1　lncRNA不同分布

lncRNA的表达不仅受转录调控因子、染色质构象及细胞状态等因素的影响，而且其在不同细胞类型、组织及生理条件下的分布表现出显著的异质性。这种异质性在很大程度上影响了lncRNA调控基因表达的效率和方式。通过分析lncRNA生成过程中的不同分布模式，可以深入探讨其在基因表达调控中的作用机制及其生物学意义。

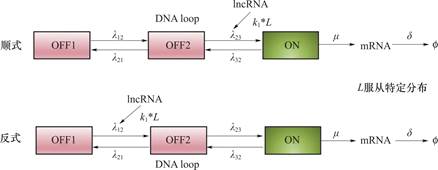
图5　L服从不同分布时顺式和反式调控图

Fig.5　Cis and Trans-Regulation Charts with L Following Different Distributions

由于lncRNA的生成与降解在细胞内表现为随机过程，其分布形式可能会受到多个因素的影响，如转录因子的活性、基因组的三维结构以及细胞的内外部环境。在这种复杂的背景下，lncRNA的分布不再是简单的均匀分布，而可能呈现出多种不同的统计分布形式，如泊松分布、负二项分布、对数正态分布等。这些分布形式的差异不仅表征了lncRNA生成的动态特性，还可能对基因表达的稳定性和噪声水平产生深远的影响^[18]。因此将lncRNA的表达量通过以下几种经典概率分布建模，不仅有助于在理论上揭示lncRNA调控机制的复杂性，还能为生物实验设计和疾病研究提供新的定量化思路。

(1)泊松分布

当 lncRNA表达的发生是一个稀疏事件(即低拷贝数)时，其表达分布可能近似泊松分布。泊松分布的特点是事件发生的平均速率λ是固定的，每个时间间隔的事件独立。在单细胞 RNA 测序中，观察到低表达的lncRNA通常接近泊松分布。这种分布也适用于转录本偶发产生的情况^[19]。

(2)负二项分布

负二项用来描述事件发生的频率，但比泊松分布的方差更大。在单细胞测序和群体细胞表达数据中，高度离散的lncRNA表达量常被认为符合负二项分布，适用于在不同细胞或组织中观察到的高异质性lncRNA表达，反映 lncRNA的生成速率和降解速率的不均衡或细胞间差异性^[20]。

(3)零膨胀负二项分布

零膨胀分布是一种修正的负二项分布，加入了零值的超额频率，适合表达量数据中大量零表达的情况。通常用于描述单细胞数据中那些在部分细胞中完全不表达或低表达的lncRNA^[21]，该模型结合了两种情况，首先是lncRNA根本没有被转录，其次表达量符合负二项分布。

(4)正态分布或对数正态分布

在群体细胞的平均表达水平上，高表达的lncRNA可能近似于正态分布，对数正态分布则用于描述基因表达数据的偏态分布情况。通常适用于转录本数量较高且稳定的lncRNA，例如某些具有显著功能的 lncRNA，在多个细胞或组织中表达均较高，并且分布接近对数正态^[22]。正态分布的特点可能反映基因表达的动态平衡，即转录和降解速率达到动态稳定。

(5)指数分布

指数分布用于描述随机事件的发生时间间隔，在特定情况下也可描述lncRNA表达量的分布，适合建模随机转录启动事件的分布以及描述低拷贝lncRNA的表达，尤其是那些稀有表达且没有显著富集的lncRNA^[23]。

(6)双峰分布

双峰分布反映基因表达具有两种主要状态，其公式如下:f(x)=ω₁f₁(x)+ω₂f₂(x)，并且f₁(x)和f₂(x)可以是任意分布(如正态分布、对数正态分布等)，权重ω₁，ω₂确保两部分贡献相加为1。双峰分布常用于描述具有两种状态的生物学系统，例如某些 lncRNA调控X染色体失活，导致某些基因在一个状态下失活，而在另一个状态下活^[24]。

4.2.2　lncRNA不同分布对mRNA表达影响

研究lncRNA服从特定的分布时，忽略lncRNA降解情况，去掉参数μ₁，σ₁，令δ=1，δ₁=1，k₁=1，μ=20，μ₁=5，随机在以下区间内取1000组值:λ₁₂∈[0.1，0.5]，λ₂₁∈[1，3]，λ₃₂∈[1，3]，λ₂₃=λ₁₂，把模拟时间设置较长时间，为t=100000，同时设定以上模型的均值和方差都为1，p值和其他参数均设为0.5，结果如图6、图7所示。

通过对lncRNA生成分布模型的分析，结合顺式和反式调控的mRNA表达结果可以得出以下结论:在大多数分布模型中，反式调控比顺式调控展现出更高的mRNA平均表达量和更低的噪声，这是可能因为反式调控通过复杂的基因调控网络提高了基因激活效率，并有效缓冲了lncRNA随机性的影响。顺式调控更依赖于局部的直接作用，其mRNA表达量较低且随机性较高。在泊松和指数分布中，反式调控的稳定性优势更为明显，而在负二项分布下，顺式调控的随机性被进一步放大，表现为更高的噪声。

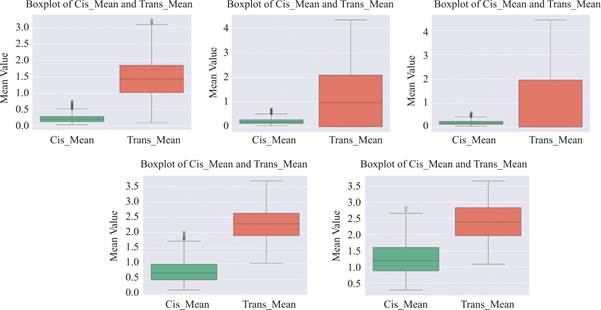
图6　lncRNA不同分布下mRNA均值箱线图

Fig.6　Box plot of mRNA mean under different distributions of LncRNA

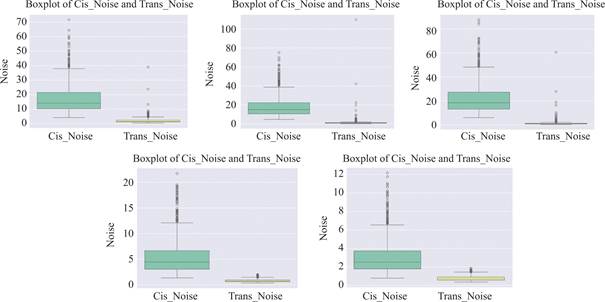
图7　lncRNA不同分布下mRNA噪声箱线图

Fig.7　Box plot of mRNA noise under different distributions of LncRNA

从分布类型对调控模式的影响可以看出，泊松分布和指数分布下mRNA表达均值较低，噪声较高，说明lncRNA在稀疏生成情境下难以实现高效调控。负二项分布在高异质性背景下展现出灵活的表达模式，但顺式调控的随机性显著增加。对数正态分布适用于稳定表达的lncRNA，反映了动态平衡中的基因调控。双峰分布描述lncRNA表达具有开关式调控模式。在生物学意义与使用场景方面，顺式调控适合短期、快速的基因表达调节，例如应对环境胁迫或信号响应。反式调控适合长期、稳定的基因网络调节，适用于多个基因的协调表达或维持基因网络的稳定性。

4.3　lncRNA转录爆发对mRNA表达影响

转录爆发(Transcriptional Bursting)是基因表达中的一种动态现象，表现为基因在短时间内快速生成大量RNA分子，随后进入较长的静默期^[25]。这一现象已被广泛观察到，尤其是在单细胞RNA测序数据中。转录爆发的本质源于基因调控中的随机性，受到调控元件的周期性激活、染色质构象变化和转录因子的动态调节的影响^[26]。

在转录爆发背景下，lncRNA生成的动态特性尤为重要，因为lncRNA生成的随机性和不均匀性会直接影响其对mRNA表达的调控效率，分析转录爆发行为对顺式和反式调控影响，可以揭示lncRNA在不同调控模式中的功能特性^[27,28]。

转录爆发行为可被建模为lncRNA生成过程的离散随机事件，本文假设lncRNA爆生成服从以下三种常见分布并给出相应数学描述:

(1)几何分布

适用于描述关注lncRNA分子生成的离散数量及每次生成事件之间的独立性时。几何分布的概率质量函数为:

P(L=k)=(1-p)^k-1p，k=1，2，3，…(11)

其中，p表示每次生成时间成功的概率。

(2)泊松分布

适用于lncRNA生成事件的均匀随机过程，适合描述低拷贝、稀疏转录的场景。泊松分布的概率质量函数为:

P(L=k)=，k≥0(12)

其中，λ表示lncRNA的平均生成速率。

(3)负二项分布

用于描述生成速率异质性较大的情况，允许高方差，适合lncRNA生成具有高动态性的情境。负二项分布的概率质量函数为:

P(L=k)-p^r(1-p)^k，k≥0(13)

其中，r是转录爆发的强度参数，p是成功概率。

在转录爆发的条件下，化学主方程需做如下修改，对于表1和表2中第7个产生lncRNA的反应，考虑其服从特定的分布而不是增加1，转录爆发生成lncRNA分别服从特定分布，均值为5，其他参数同样固定为μ=20，σ=1，k₁=1，λ₁₂=0.3，λ₂₁=1.2，λ₃₂=2.5，λ₂₃=λ₁₂的值，模拟时间设置为t=100000，随机在以下区间内取1000组值:λ₁₂∈[0.1，0.5]，λ₂₁∈[1，3]，λ₃₂∈[1，3]，λ₂₃=λ₁₂，此时顺式和反式调控的均值和噪声分布如图8所示。

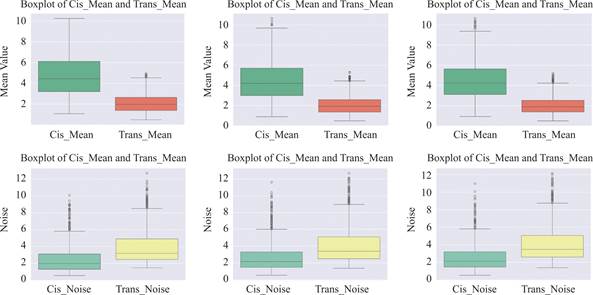
图8　lncRNA为几何分布式、泊松分布式和负二项转录爆发时顺式和反式调控箱线图

Fig.8　Box plot under Cis and Trans-Regulation for geometric，poisson， and negative binomial distribution of LncRNA during transcriptional bursts

根据随机生成的参数可以看到，相比原始模型，在转录爆发情况下，顺式调控下mRNA均值变大，反式调控下mRNA的均值反而减小了，且顺式调控下mRNA的均值会大于反式调控，顺式调控的噪声也会大于反式调控，这说明转录爆发对于顺式反式调控下的mRNA的表达具有显著影响。此外对于不同分布的lncRNA转录爆发，顺式和反式调控的mRNA表达箱线图基本没有差异，说明lnRNA转录爆发分布形式的不同对mRNA表达的影响有限。

5　结论

本研究从顺式与反式调控的视角，系统地探讨了lncRNA调控基因表达的动态特性，验证了SSA和FSP算法捕捉小分子系统动态特点的准确性，建模分析研究表明，顺式调控和反式调控在基因表达的稳定性和效率上展现了显著差异:反式调控更适合长效且稳定的基因网络调节，而顺式调控则在局部快速响应中占优。此外通过对lncRNA生成分布的深入分析，发现lncRNA的表达异质性对mRNA表达的动态特性有重要影响。转录爆发的引入进一步揭示了基因表达调控的复杂性。在转录爆发情境下，顺式调控的优势更为明显，其调控效率和表达水平均显著均超过反式调控，这一现象可能暗示了顺式调控在特定环境或刺激下的重要作用。同时对于lncRNA生成分布的选择性研究表明，不同分布形式的调控效能差异有限，但在特定的生物学背景中可能具有独特意义。

总而言之，本文通过数学建模与随机模拟算法，对lncRNA的调控机制进行分析，深化了lncRNA对基因表达调控机制的理解，为探索lncRNA的作用提供了新的研究思路。

利益冲突: 作者声明无利益冲突。

---

^[③] *通讯作者　Corresponding author:黄丽芳，hlifang@gdufe.edu.cn
收稿日期:2025-01-25;　录用日期:2025-02-10;　发表日期:2025-03-28

参考文献(References)

[1] Mercer T R, Dinger M E, Mattick J S. Long non-coding RNAs: insights into functions[J]. Nat. Rev. Genet. , 2009, 10(3): 155-159.
https://doi.org/10.1038/nrg2521
[2] Brockdorff N, Bowness J S, Wei G. Progress toward understanding chromosome silencing by Xist RNA[J]. Genes & development, 2020, 34(11-12): 733-744.
https://doi.org/10.1101/gad.337196.120
[3] Senmatsu S, Hirota K. Roles of lncRNA transcription as a novel regulator of chromosomal function[J]. Genes & genetic systems, 2020, 95(5): 213-223.
https://doi.org/10.1266/ggs.20-00024
[4] Tan Y T, Lin J F, Li T, et al. LncRNA-mediated posttranslational modifications and reprogramming of energy metabolism in cancer[J]. Cancer Communications, 2021, 41(2): 109-120.
https://doi.org/10.1002/cac2.12108
[5] Ferrer J, Dimitrova N. Transcription regulation by long non-coding RNAs: mechanisms and disease relevance[J]. Nature Reviews Molecular Cell Biology, 2024, 25(5): 396-415.
https://doi.org/10.1038/s41580-023-00694-9
[6] Engreitz J M, Haines J E, Perez E M, et al. Local regulation of gene expression by lncRNA promoters, transcription and splicing[J]. Nature, 2016, 539(7629): 452-455.
https://doi.org/10.1038/nature20149
[7] Johnsson P, Ziegenhain C, Hartmanis L, et al. Transcriptional kinetics and molecular functions of long noncoding RNAs[J]. Nature Genetics, 2022, 54(3): 306-317.
https://doi.org/10.1038/s41588-022-01014-1
[8] Grossi E, Raimondi I, Goñi E, et al. A lncRNA-SWI/ SNF complex crosstalk controls transcriptional activation at specific promoter regions[J]. Nature Communications, 2020, 11(1): 936.
https://doi.org/1038/s41467-020-14623-3
[9] Gao F, Cai Y, Kapranov P, et al. Reverse-genetics studies of lncRNAs—what we have learnt and paths forward[J]. Genome biology, 2020, 21: 1-23,
https://doi.org/10.1186/s13059-020-01994-5
[10] Ørom U A, Shiekhattar R. Long noncoding RNAs usher in a new era in the biology of enhancers[J]. Cell, 2013, 154(6): 1190-1193.
https://doi.org/10.1016/j.cell.2013.08.028
[11] Melé M, Rinn J L. “Cat’s Cradling” the 3D genome by the act of LncRNA transcription[J]. Molecular Cell, 2016, 62(5): 657-664.
https://doi.org/10.1016/j.molcel.2016.05.011
[12] Amicone L, Marchetti A, Cicchini C. The lncRNA HOTAIR: a pleiotropic regulator of epithelial cell plasticity[J]. Journal of Experimental & Clinical Cancer Research, 2023, 42(1): 147.
https://doi.org/10.1186/s13046-023-02725-x
[13] Siciliano V, Garzilli I, Fracassi C, et al. MiRNAs confer phenotypic robustness to gene networks by suppressing biological noise[J]. Nature communications, 2013, 4(1): 2364.
https://doi.org/10.1038/ncomms3364
[14] Martirosyan A, Figliuzzi M, Marinari E, et al. Probing the limits to microRNA-mediated control of gene expression[J]. PLoS computational biology, 2016, 12(1): e1004715.
https://doi.org/10.1371/journal.pcbi.1004715
[15] Grima R, Esmenjaud P M. Quantifying and correcting bias in transcriptional parameter inference from singlecell data[J]. Biophysical Journal, 2024, 123(1): 4-30.
https://doi.org/10.1016/j.bpj.2023.10.021
[16] Warne D J, Baker R E, Simpson M J. Simulation and inference algorithms for stochastic biochemical reaction networks: from basic concepts to state-of-the-art[J]. Journal of the Royal Society Interface, 2019, 16(151): 20180943.
https://doi.org/10.1098/rsif.2018.0943
[17] Jiao F, Li J, Liu T, et al. What can we learn when fitting a simple telegraph model to a complex gene expression model?[J]. PLOS Computational Biology, 2024, 20(5): e1012118.
https://doi.org/10.1371/journal.pcbi.1012118
[18] Chen L, Zhu C, Jiao F. A generalized moment-based method for estimating parameters of stochastic gene transcription[J]. Mathematical Biosciences, 2022, 345: 108780.
https://doi.org/10.1016/j.mbs.2022.108780
[19] Mattick, Amaral, Carninci. Long non-coding RNAs: definitions, functions, challenges and recommendations[J]. Nature Reviews Molecular Cell Biology, 2023, 24(6): 430-447.
https://doi.org/10.1038/s41580-022-00566-8
[20] Bridges M C, Daulagala A C, Kourtidis A. LNCcation: lncRNA localization and function[J]. Journal of Cell Biology, 2021, 220(2): e202009045.
https://doi.org/10.1083/jcb.202009045
[21] Fang K, Huang W, Sun Y M, et al. Cis-acting lnc-eRNA SEELA directly binds histone H4 to promote histone recognition and leukemia progression[J]. Genome Biology, 2020, 21: 1-23.
https://doi.org/10.1186/s13059-020-02186-x
[22] Gil N, Ulitsky I. Regulation of gene expression by cisacting long non-coding RNAs[J]. Nature Reviews Genetics, 2020, 21(2): 102-117.
https://doi.org/10.1038/s41576-019-0184-5
[23] Saleh R O, Al-Ouqaili M T S, Ali E, et al. lncRNA-microRNA axis in cancer drug resistance: particular focus on signaling pathways[J]. Medical Oncology, 2024, 41(2): 52.
https://doi.org/10.1007/s12032-023-02263-8
[24] Hou T Y, Kraus W L. Spirits in the material world: enhancer RNAs in transcriptional regulation[J]. Trends in biochemical sciences, 2021, 46(2): 138-153.
https://doi.org/10.1016/j.tibs.2020.08.007
[25] Gong C, Fan Y, Zhou X, et al. Comprehensive analysis of expression and prognostic value of GATAs in lung cancer[J]. Journal of Cancer, 2021, 12(13): 3862.
https://doi.org/10.7150/jca.52623
[26] Zhou, Liang, Dan R Littman. Transcriptional Regulatory Networks in Th17 Cell Differentiation[J]. Current Opinion in Immunology, 2009, 21(2): 146-152.
https://doi.org/10.1016/j.coi.2009.03.001
[27] Tunnacliffe, Edward, Adam M. Corrigan, and Jonathan R. Chubb. Promoter-Mediated Diversification of Transcriptional Bursting Dynamics Following Gene Duplication[J]. Proceedings of the National Academy of Sciences of the United States of America, 2018, 115(33): 8364-8369.
https://doi.org/10.1073/pnas.1800943115
[28] Huang L, Yuan Z, Liu P, et al. Feedback-induced counterintuitive correlations of gene expression noise with bursting kinetics[J]. Physical Review E, 2014, 90(5): 052702.
https://doi.org/10.1103/physreve.90.052702
[29] Liu T, Zhang J, Zhou T. Effect of interaction between chromatin loops on cell-to-cell variability in gene expression[J]. PLoS computational biology, 2016, 12(5): e1004917.
https://doi.org/10.1371/journal.pcbi.1004917

Differential Analysis of Cis-and Trans-Regulation of Gene Expression by LncRNA

OUYANG Jianzhi, XIAO Jiayi, CHEN Zhubin, LIAO Xiaoyu, HUANG Lifang^*

(School of Statistics and Mathematics, Guangdong University of Finance & Economics, Guangzhou 510320, China)

Abstract: Research has shown that long non-coding RNAs (lncRNAs) are involved in the regulation of essential biological processes at multiple levels. However so far, the mechanisms of gene expression regulation by lncRNAs and their biological functions are not yet fully understood. This study focuses on the differences in gene expression regulation by lncRNAs through cis-and trans-regulation and their dynamic behaviors. First, a mathematical model for the functional action of lncRNAs is established based on chemical master equations, and the accuracy of the SSA and FSP algorithms is validated. Second, the distribution of lncRNAs and the effect of transcriptional bursts on gene expression are analyzed using SSA and FSP algorithms. This paper combines dynamical system theory and stochastic simulation methods to first construct the model of lncRNA regulatory mechanisms based on experimental results; Then some key indicators ( such as the probability distribution, mean, and noise of mRNA) are then calculated to analyze the dynamic properties exhibited by lncRNAs in cis-and trans-regulation. The study shows that under the original model, trans-regulation leads to higher mRNA expression levels and lower noise, while cis-regulation is more sensitive to rapid local responses. The impact of the lncRNA generation distribution on the dynamic characteristics of mRNA expression is also studied, and it is found that different distribution forms significantly affect the stability and efficiency of the regulatory pattern. After adding transcriptional bursts, cisregulation results in higher average mRNA expression levels and lower noise compared to trans-regulation. This study provides theoretical support for a comprehensive understanding of lncRNA regulatory mechanisms and their functional characteristics in gene expression, offering a new perspective for exploring lncRNA regulatory mechanisms.  

Keywords: lncRNA, Cis-regulation, Trans-regulation, transcription burst

DOI: 10.48014/jcss.20250125001

Citation: OUYANG Jianzhi, XIAO Jiayi, CHEN Zhubin, et al. Differential analysis of Cis-and Trans-Regulation of gene expression by LncRNA[J]. Journal of Chinese Statistical Sciences, 2025, 3(1): 26-38.