随机基因表达模型中表达产物数量分布形态的判别条件

丘芷珊, 盛英, 焦锋^*

(广州大学数学与信息科学学院, 广州 510006)

摘要: 基因表达本质上是一个随机过程。表达产物数量分布能够全面刻画基因表达的随机行为, 通常呈现出递减、钟形和双峰三种分布形态。文献[21]探讨了耦合最小正负反馈回路的随机基因表达模型, 通过在参数平面上构造两条连续曲线C1和C2, 从理论上给出了模型产生三种分布形态的充分必要条件。然而, 对于任意给定的一组参数, 由于曲线C1和C2无法给出精确表达式, 很难直接并且快速地判断耦合最小正负反馈回路的随机基因表达模型能够产生何种分布形态. 这极大影响了我们利用数学模型针对海量单细胞转录数据的研究. 在该文中, 我们通过对曲线C1和C2的定量刻画, 给出若干产生三种分布形态的系统参数条件。这些参数条件可通过简单的初等函数进行计算, 因此提供了判断随机基因表达模型中表达产物数量分布形态的快速判别方法。

关键词: 随机基因表达模型, 正负反馈回路, 化学反应主方程, 表达产物数量分布

DOI: 10.48014/jcss.20250201001

引用格式: 芷珊, 盛英, 焦锋. 随机基因表达模型中表达产物数量分布形态的判别条件[J]. 中国统计科学学报, 2025, 3(1): 15-25.

文章类型: 研究性论文

收稿日期: 2025-02-01

接收日期: 2025-02-10

出版日期: 2025-03-28

1　引言

基因表达是遗传信息在细胞内转录并翻译成功能性蛋白质的过程，是遗传信息流中的关键步骤。基因表达的调控对于细胞功能和生物体的发育至关重要，其异常与多种疾病的发生和发展相关^[1,2]。在过去二十年中对单细胞水平的广泛研究表明，基因表达是一个随机过程^[3,4]，表现为同源细胞群中mRNA或蛋白质的数量^[3]。最早的随机基因表达动力学模型之一是两状态模型^[5]，它描述了mRNA或蛋白质的合成和降解过程。然而在活细胞中，一个基因的表达通常会与其他基因的表达有关，这就形成了各种各样的基因调控网络^[6]。最常见的网络之一是自调控基因反馈回路，其中从一个基因中产生的蛋白质反过来促进或者抑制该基因的表达^[7]。据估计，在大肠杆菌中大约有40%的转录因子自调控^[8]，其中大部分是负调控的^[7]。

过去的二十年中，许多学者对这些基因调控网络进行数学建模，并发展了一系列自调控基因表达的分析理论^[9-11]。在这种情况下，蛋白质数量的稳态分布能够被精确求解^[9-11]。实验上发现蛋白质数量的稳态分布能产生三种分布形态:递减分布(只有一个零峰)、钟形分布(只有一个非零峰)和双峰分布(含有两个峰)^[12]。递减分布和钟形分布表明了一个等基因细胞群的表型同质性，而双峰分布表明了一种内在调节机制，其中该机制能随机引导细胞进入两种不同的表型^[13-15]。虽然自调控的分析理论已经得到了很好的发展，但是蛋白质分布的精确表达式通常会涉及各种各样特殊的函数。若蛋白质的表达一次只产生一个，那么蛋白质分布的表达式会涉及合流超几何函数^[16,17];若蛋白质的表示是爆发的，那么表达式会包含高斯超几何函数^[18,19]。由于缺乏关于超几何函数的单调性结论，所以大部分情况下只能通过数值模拟来确定蛋白质分布的类型。文献[20]首次用数学的语言严格证明了两状态模型能产生并且只能产生这三种分布形态，并给出了产生这三种分布形态的充分必要条件。紧接着，文献[21]将这种严格分类推广到了带有正负反馈的最小耦合基因回路。他们都是通过构建两条连续递增的曲线C₁和C₂来确定分布形态和参数区域的一一对应关系。然而这两条曲线是利用一系列含有合流超几何函数的比率算子的等高线进行几何构建得到的，因此我们很难知道曲线C₁和C₂的显式表达式。于是在给定参数集的情况下，很难能够直接且快速地知道它会产生何种分布。事实上，在给定参数集的情况下，能够直接并且快速地判断模型产生的分布类型是非常有用的:①在生物技术领域，如合成生物学和基因工程，快速判断分布类型可以优化基因回路的设计，提高生产效率;②在基础生物学研究中，快速判断分布类型可以加速对基因调控网络的理解，这有助于揭示生物体内复杂的调控机制，为进一步的生物学研究提供基础等。

因此，基于文献[21]，本文考虑带有正负反馈的最小耦合基因回路，并给出了该模型产生递减分布、钟形分布或双峰分布的一些条件。这些条件在某种程度上使得我们在给定参数集的情况下能够直接并且快速地判断带有正负反馈的最小耦合基因产生的分布类型。这个模型包含最经典的自调控模型作为特例。在第二部分首先介绍带有正负反馈的最小耦合基因回路的化学反应和化学主方程，并给出了一些准备知识。在第三部分分别给出了产生递减分布、钟形分布和双峰分布的一些条件。在第四部分进行了总结。

2　预备知识

本文研究最小耦合正负反馈模型中的随机基因表达，这包含基因切换，蛋白质的生成以及蛋白质的降解(见图1a)。令G和G^*表示基因的活跃态和非活跃态，P表示对应的蛋白质，n表示蛋白质的数量。当基因处于活跃态时，才会产生蛋白质。于是耦合反馈回路的化学反应可以写成如下形式^[22]:

GG^*，G^*G，G^*G^*+P，Pϕ，(1)

其中，a和b表示基因的切换速率，μ和ν分别表示正反馈和负反馈强度，s表示基因在活跃态时生成蛋白质的速率，d表示蛋白质的降解速率。由于反馈调控，蛋白质的数量n会直接或间接的影响基因的切换速率。方便起见，通常令d=1。值得注意的是，当负反馈强度ν=0时，此时模型就会变成正反馈模型;当正反馈强度μ=0时，此时模型时负反馈模型;当正负反馈强度μ，ν=0时，此时模型是两状态模型。因此本文的所有结论都适用于上述所有模型。

基因的微观状态可以由有序对(i，n) 表示。其中基因状态i=0，1分别表示基因的活跃态和非活跃态。令P_i，n(t)表示在单细胞中当基因处于i状态时在t时刻产生n个蛋白质的概率.那么随机基因表达动力学可以写成如下的化学主方程形式:

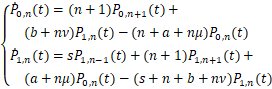(2)

其中，P_1，-1(t)=0。令P_n(t)=P_0，n(t)+P_1，n(t)表示t时刻产生n个蛋白质的概率。且P_n=P_n(t)表示稳态时产生n个蛋白质的概率。通过求解化学主方程(2)，可得蛋白质数量的稳态分布解析式^[22,23]:

P_n=(3)

其中 (x)_n=x(x+1)…(x+n-1)表示阶乘幂，₁F₁(α;β;z)是合流超几何函数，且常数α=，β=+，ω=，z₀=.

文献[21]中的引理3.1将化学主方程(2)转换成P_n-1，P_n和P_n+1之间的递归表达式:

n(n+1)P_n+1+sP_n-1-
nP_n=0(4)

其中n≥1。作者们利用上述递归表达式在定理3.2中证明了P_n只能产生三种分布形态:(1)递减分布(P_n单调下降，因此只有一个零峰);钟形分布(P_n先上升后下降，因此只有一个非零峰);双峰分布(P_n含有一个零峰和一个非零峰)(见图1b)。接着引入差分算子ΔP_n=P_n-P_n-1，则等式(4)可重新写成如下的非自治的二阶差分方程:

n(n+1)ΔP_n+1=
sΔP_n+Q_nP_n(5)

其中

Q_n=n(a-1-μ+b-1-ν-sμ)+
n²(μ+ν)-s(a-1-μ)，n≥1(6)

文献[11]还定义了一个比率算子:

θ_n=，n≥1，

并在引理4.1中证明了对所有的n≥1，有θ_n<s/n，以及在引理4.3中证明了对任意给定的s>0和μ，ν≥0，θ_n(a，b)关于a严格单调递增，关于b严格单调递减。

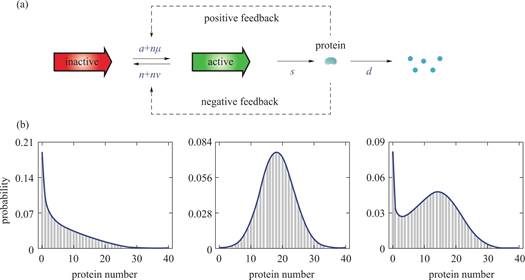
图1　带反馈的基因调控网络和分布形态

(a)带有正负反馈的最小耦合基因回路。基因启动子在活跃态和非活跃态之间自发的切换速率为a和b。当基因在活跃态时，蛋白质的生成速率为s，然而生成的蛋白质会反过来促进或抑制其自身的表达，其中正反馈强度为μ，负反馈强度为ν。翻译过程仅仅发生在活跃态。蛋白质的个数为n以及蛋白质降解速率为d。(b)该模型能产生三种不同的稳态蛋白质数量的分布形态:递减分布(P_n关于n单调递减，因此只有一个零峰);钟形分布(P_n关于n先上升后下降，因此只有一个非零峰);双峰分布(P_n有一个零峰和一个非零峰)。左边图(递减分布)的参数为s=30，d=1，a=0.5，b=0.4，μ=0，ν=0.1，中间图(钟形分布)的参数为s=30，d=1，a=1，b=0.1，μ=0.8，ν=0.5，右边图(双峰分布)的参数为 s=30，d=1，a=0.4，b=0.1，μ=0.2，ν=0.2。

Fig.1　Gene regulatory network with feedback and distribution patterns

(a)A minimal coupled gene circuit with positive-plus-negative feedback.The gene promoter spontaneously switches between the active and inactive states with rates of a and b.When the gene is in the active state，the protein synthesis rate is s，but the produced protein can feedback to either promote or inhibit its own expression，with positive feedback strength u and negative feedback strength v.Translation occurs only in the active state.The number of proteins is n，and the degradation rate of the protein is d.(b)The model can generate three different shapes of steady-state protein distributions:a decreasing distribution(P_n is monotonically decreasing with respect to n，resulting in a single zero peak);a bell-shaped distribution(P_n first increases and then decreases with respect to n，resulting in a single non-zero peak);and a bimodal distribution(P_n has both a zero peak and a non-zero peak).The parameters are chosen as s=30，d=1，a=0.5，b=0.4，μ=0，ν=0.1 for the left panel，s=30，d=1，a=1，b=0.1，μ=0.8，ν=0.5 for the middle panel，and s=30，d=1，a=0.4，b=0.1，μ=0.2，ν=0.2 for the right panel.

3　结论

由文献[21]中的定理4.2可知，当s≤1时，P_n只能产生递减分布。因为蛋白质的合成速率s 表示基因处于活跃态时产生的平均蛋白质个数，所以s≤1的情况是十分罕见的。于是接下来我们需要考虑一种更典型和更常见的情况s>1。

定理1　若a≥1+μ，则P_n要么是递减分布要么是钟形分布。

证明　由于P_n只能产生递减分布、钟形分布和双峰分布^[21]，因此只需证明当a≥1+μ时，P_n不是双峰分布。利用反证法，假设P_n是双峰分布，则由双峰的定义可知存在唯一一个极大值点n^*≥2 满足

Δ=->0，
Δ=-≤0，(7)

以及存在一个极小值点n_l∈(0，n^*)满足

Δ=-≤0，
Δ=-≥0.(8)

将等式(7)和等式(8)分别带入等式(5)中，发现<0以及≥0。再将a≥1+μ和n=0带入等式(6)中，发现Q₀≤0。由于Q_n是凸函数，因此对所有的n∈(0，n^*]，有Q_n<0。这与≥0，n_l∈(0，n^*)矛盾。因此当a>1+μ，则P_n要么是递减分布要么是钟形分布。

下面将给出P_n产生递减分布的一些条件。

引理1

(Ⅰ)当2-b+μ+ν+sμ≤a≤1+μ时，对所有的n≥1，有P_n-1>P_n。

(Ⅱ)当-b+2+sμ≤a≤(b+s-2)/(s-1)时，P_n是递减分布。

(Ⅲ)当1+μ≤a≤b/(s-1)时，P_n是递减分布。

证明　(Ⅰ)将2-b+μ+ν+sμ≤a≤1+μ带入等式(6)中，发现对所有的n≥1，有Q_n>0或者Q_n≡0。注意到Q_n≡0当且仅当a=1+μ，b=1+ν+sμ以及μ，ν=0，否则Q_n>0。首先，考虑Q_n≡0，n≥1的情况。将a=1+μ，b=1+ν+sμ以及μ，ν=0带入等式(5)中，可得

n(n+1)ΔP_n+1=ΔP_n，n≥1.

接下来证明对所有的n≥1，有P_n-1>P_n。利用反证法，由上式可知，若存在某个n^*≥1，使≥0，则对所有的n≥n^*，有ΔP_n≥0，即P_n≥P_n-1。事实上，当n≥1时，有θ_n=P_n/P_n-1<s/n，这也就意味着当n≥s时，有P_n<P_n-1。这产生了矛盾。接下来考虑Q_n>0，n≥1的情况。还是利用反证法，由于文献[21]的定理3.2表明P_n至多只能产生两个峰，要么在n=0处，要么在n=n₁>0处，因此假设存在点n^*≥1满足:

Δ=-≥0，
Δ=-≤0.

将上述式子带入等式(5)，发现≤0，其中n^*≥1。这产生了矛盾。由此得出结论:当2-b+μ+ν+sμ≤a≤1+μ时，对所有的n≥1，有P_n-1>P_n。

(Ⅱ)因为s>1，所以由等式(6)可知a≤(b+s-2)/(s-1)和a≥-b+2+sμ分别意味着Q₁≥0和Q₁≥Q₀。再次利用Q_n的表达式(6)可知当-b+2+sμ≤a≤(b+s-2)/(s-1)时，有Q_n≥0，其中n≥1。接下来利用反证法，假设当1+μ≤a≤(b+s-2)/(s-1)时，P_n存在一个非零峰n^*≥1，使得等式(7)成立。于是由等式(5)可知<0，n^*≥1。这产生了矛盾，得证。

(Ⅲ)利用θ_n=P_n/P_n-1<s/n，n≥1，将sP_n代替等式(4)中的(n+1)P_n+1，那么有

nP_n

<sP_n-1，n≥1.

这表明P_n/P_n-1<1，若

≤1，n≥1.

即

s≤
=n+，n≥1.

令

g(x)=x+，x∈[1，¥).

对x求导，得

g'(x)=1+，x∈[1，¥).

当a≥1+μ时，有g'(x)>0，即g(x)在x∈[1，¥)上单调递增。因此当a≥1+μ时，

g(x)≥g(1)=1+，x≥1，

其中g(1)是g(x)的最小值。于是当a≥1+μ且s≤1+b/a时，P_n是递减分布。得证。

易发现引理1中的条件(Ⅰ)始终包含在条件(Ⅱ)中，但是条件(Ⅰ)确保了P_n是严格单调递减的，条件(Ⅱ)无法保证这一点。

定理2

(Ⅰ)当1<s≤2，a≤b/(s-1)且b≥(1+μ)(s-1)时，P_n是递减分布。

(Ⅱ)当s>2，a≤(b+s-2)/(s-1)且b≥1+(s-1)μ时，P_n是递减分布。

证明　由引理1 中的(Ⅱ)可知当a=1+μ且b=(1+μ)(s-1)时，P_n是递减分布。由θ_n的定义可知

θ_n(1+μ，(1+μ)(s-1))=

≤1，n≥1.

文献[21]中的引理4.3 证明了θ_n(a，b)=P_n(a，b)/P_n-1(a，b)关于a严格单调递增，关于b严格单调递减。于是对任意的a≤1+μ及b≥(1+μ)(s-1)，有

θ_n(a，b)≤θ_n(1+μ，b)≤

θ_n(1+μ，(1+μ)(s-1))≤1，n≥1.

因此当a≤1+μ及b≥(1+μ)(s-1)时，P_n是递减分布。结合引理1中的(Ⅱ)，发现当a≤b/(s-1)且b≥(1+μ)(s-1)时，P_n是递减分布。

易发现直线a=-b+2+sμ与直线a=(b+s-2)/(s-1)相交于点(a，b)=(1+μ，1+(s-1)μ)。利用引理1中的(Ⅰ)可知当a=1+μ且b=1+(s-1)μ时，P_n是递减分布。再次利用θ_n(a，b)的定义和它关于a，b的单调性，发现a≤1+μ及b≥1+(s-1)μ，有

θ_n(a，b)≤θ_n(1+μ，b)≤

θ_n(1+μ，1+(s-1)μ)≤1，n≥1.

因此当a≤1+μ及b≥1+(s-1)μ时，P_n是递减分布。当b≥1+(s-1)μ时，-b+2+sμ≤1+μ。结合引理1中的(Ⅱ)，发现当a≤(b+s-2)/(s-1)且b≥1+(s-1)μ时，P_n是递减分布。

当1<s≤2时，直线a=(b+s-2)/(s-1)在直线a=b/(s-1)的下方以及直线b=1+(s-1)μ在直线b=(1+μ)(s-1)的右方，于是当a≤b/(s-1)且b≥(1+μ)(s-1)时，P_n是递减分布。(Ⅰ)得证。当s>2时，直线a=(b+s-2)/(s-1)在直线a=b/(s-1)的上方以及直线b=1+(s-1)μ在直线b=(1+μ)(s-1)的左方，于是当a≤(b+s-2)/(s-1)且b≥1+(s-1)μ时，P_n是递减分布。(Ⅱ)得证。

下面的定理将给出P_n产生钟形分布的一些条件。

定理3

(Ⅰ)当a>(b+s)/(s-1)时，P_n是钟形分布。

(Ⅱ)当s≥1+ν/(1+μ)且a≥(b+s)(1+μ)/ν时，P_n是钟形分布。

证明(Ⅰ)因为P_n至多只能产生两个峰，要么在n=0处，要么在n=n₁>0处[21]，所以当P₀<P₁时，P_n一定是钟形分布。将n=1带入P_n的递归表达式(4)中，可得

(a+b+s)P₁-saP₀>0，

则

=.

因此当(a+b+s)/sa<1，有P₀<P₁。这就意味着当a>b/(s-1)+s/(s-1)时，P_n是钟形分布，且唯一的峰在n≥1处。

(Ⅱ)由合流超几何函数的等价方程[]可知下列等式成立:

(β+n-1)(β+n)₁F₁(α+n-1;β+n-1;-ωz₀)=-ωz₀(α+n)₁F₁(α+n+1;β+n+1;-ωz₀)+(β+n)(β+n-1+ωz₀)₁F₁(α+n;β+n;-ωz₀)，

其中

α=，

β=+，

ω=，

z₀=.

因为上式等式的右边的第一项小于0，所以

(β+n-1+ωz₀)₁F₁(α+n;β+n;-ωz₀)>

(β+n-1)₁F₁(α+n-1;β+n-1;-ωz₀)，

即

>

.

令β₀=β+ωz₀=(a+b+s)/(1+μ+ν)。由上述关系式和P_n的表达式(3)可知，当α≥β₀，即a≥(b+s)(1+μ)/ν时，

=··

>

·≥.

若ω≥n，则P_n>P_n-1。特别地，当ω=s(1+μ)/(1+μ+ν)≥1，有P₁>P₀。因此当s≥1+ν/(1+μ)且a≥(b+s)(1+μ)/ν时，P_n是钟形分布。证明结束。

事实上，当s≥1+ν/(1+μ)时，有1/(s-1)≤(1+μ)/ν，因此定理3中的条件(Ⅱ)会始终包含在条件(Ⅰ)中。由文献[21]中的定理4.4可知，s>2是产生双峰的必要条件。因此当1<s≤2时，P_n不会产生双峰分布，即P_n是递减分布或者钟形分布。结合定理1，定理2和定理3，可以得到图2。

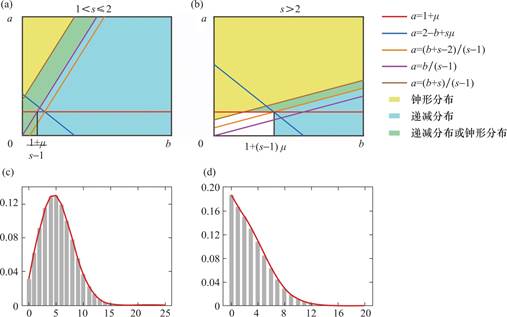
图2　蛋白质数量分布形态在b-a平面的示意图

(a)当1<s≤2时，递减分布和钟形分布在b-a平面上的划分。(b)当s>2时，递减分布和钟形分布在b-a平面上的划分。(c)钟形分布，参数为s=10，d=1，a=2，b=1，μ=0.1，ν=0.2。(d)递减分布，参数为s=10，d=1，a=1，b=2，μ=0.1，ν=0.2

Fig.2　Schematic diagram of the distribution shapes of protein number in the b-a plane

(a)When 1<s≤2，the division of decaying distribution and bell shaped distribution in the b-a plane.(d)When s>2，the division of decaying distribution and bell-shaped distribution in the b-a plane.(c)Bell shaped distribution.The parameters are s=10，d=1，a=2，b=1，μ=0.1，ν=0.2;(d)Decaying distribution.The parameters are chosen as s=10，d=1，a=1，b=2，μ=0.1，ν=0.2.

观察图2，可以发现只有图2b的空白区域才有可能出现双峰分布。这意味着当s>2，b<1+(s-1)μ，a<min {(b+s)/(s-1)，1+μ}时，P_n才有可能是双峰分布。

定理4　当s=1+ν/(1+μ)时，若a>(b+s)(1+μ)/ν，则P_n是钟形分布;若a≤(b+s)(1+μ)/ν，则P_n是递减分布。

证明　若a=(1+μ)b/ν+1，由α，β的表达式可知α=β。根据P_n的表达式(3)，发现

=e^-ω.

当s=1+ν/(1+μ)时，有ω=1。于是由θ_n(a，b)的定义可知

θ₁=

=ω=1，

且

θ_n=

=<1，n≥2.

当a>(1+μ)b/ν+1时，由θ_n关于a的单调性可知，

θ₁(a，b)>θ₁=1.

这表明当a>(1+μ)b/ν+1时，有P₁>P₀，即P_n是钟形分布。当a≤(1+μ)b/ν+1时，由θ_n关于a的单调性可知

θ₁(a，b)≤θ₁=

1，θ_n(a，b)≤θ_n(+1，b)<1，n≥2.

这表明，当a≤(1+μ)b/ν+1时，有P_n≤P_n-1，n≥1，即P_n是递减分布。证明完毕。

定理5　设ν≪1且固定μ=μ^*>0和a=a^*<1。对任意的n_l∈[1，1+(1-a^*)/μ^*)，只要s>n_l，就存在b=b^*<1+sμ^*使得P_n是双峰分布，且在n_l处取得极小值，在n^*处取得极大值，其中n^*满足<0，n<s。

证明　令ν≪1，则z₀=1/(1+μ)，ω=s。在接下来的讨论中，将P_n和Q_n重新写作P_n(a，b，μ，s)和Q_n(a，b，μ，s)。令

(s)=e^-s.

当n<s时，有(s)/(s)=s/n>1，因此(s)>(s)，其中1≤n_l<s。当b→0时，有P_n(a^*，b，μ^*，s)→(s)，于是存在充分小的Δb>0使得对任意的b∈(0，Δb)，有

Δ(a^*，b，μ^*，s)=

(a^*，b，μ^*，s)-(a^*，b，μ^*，s)>0.

由定理1(Ⅰ)可知

Δ(a^*，1+sμ^*，μ^*，s)<0.

利用θ_n关于b的单调性[21]，发现存在∈[Δb，1+sμ^*)使得对所有的b∈(0，)，有

Δ(a^*，，μ^*，s)=0，Δ(a^*，b，μ^*，s)>0.

若n_l<1+(1-a^*)/μ^*，则有μ^*n_l+(a^*-1-μ^*)<0。结合s>n_l，于是有

s>n_l>，

且

μ^*+(a^*-2-μ^*-sμ^*)n_l-

s(a^*-1-μ^*)>0.

则

(a^*，，μ^*，s)=

μ^*+(a^*-2-μ^*-sμ^*)n_l-

s(a^*-1-μ^*)+n_l>0.

将上式和Δ(a^*，，μ^*，s)=0带入等式(5)中，发现Δ(a^*，，μ^*，s)<0。若b^*∈(0，)充分接近，则

Δ(a^*，b^*，μ^*，s)<0，

Δ(a^*，b^*，μ^*，s)>0.

因此P_n(a^*，b^*，μ^*，s)在n=n_l处取得极小值，其中两个峰分别在n=0和n=n^*>n_l处。

由等式(5)和(7)以及P_n(a^*，b^*，μ^*，s)的第二个峰在n=n^*处可知Q_n(a^*，b^*，μ^*，s)<0。又因为θ_n<s/n，所以

1≤<，

这就意味着n^*<s。证毕。

在接下来的定理中，考虑负反馈强度ν和正反馈强度μ充分大时，对P_n分布形态的影响。

定理6　固定a，b，s>0且μ≥0，存在ν^*使得当ν>ν^*时，下列性质成立:

(Ⅰ)若a>(b+s)/(s-1)，则P_n是钟形分布。

(Ⅱ)若a≤(b+s)/(s-1)，则P_n是递减分布。

证明　固定a，b，s>0且μ≥0。由P_n的表达式(3)可知

=··

=·，(9)

其中n≥1且

α=，

β=+，

ω=，z₀=.

由α，β的表达式，发现

<1.

结合ω，z₀的表达式，有z₀≤1且

=

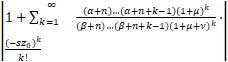
<1+≤1+=e^s.(10)

利用Lebesgue 控制收敛定理可知

=1+.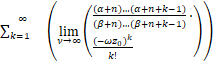

结合上式与等式(9)发现当n=1时，

=.

若sa/(a+b+s)>1，则P₁>P₀。这意味着存在充分大的ν^*使得当ν>ν^*，且a>(b+s)/(s-1)时，P_n是钟形分布。(Ⅰ)得证。若sa/(a+b+s)≤1，则P₁≤P₀。接下来说明当n≥2时，有P_n≤P_n-1，就能证明(Ⅱ)成立。事实上，当n≥2时，

=0<1.

这表明当ν>ν^*时，对所有的n≥2时，有P_n<P_n-1。(Ⅱ)得证。

定理7　固定a，b，s>0且ν≥0，存在μ^*使得当μ>μ^*，下列性质成立:

(Ⅰ)若a≥b/(s-1)，则P_n是钟形分布。

(Ⅱ)若a<b/(s-1)，则P_n是双峰分布。

证明　固定a，b，s>0且ν≥0。结合等式(10)和Lebesgue 控制收敛定理可知

=1+.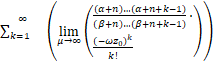

结合上式与等式(9)发现当n=1时，

=

以及当n≥2时，

=s>1.(11)

若sa/(a+b)>1，则P₁>P₀。这表明存在充分大的μ^*使得当μ>μ^*且a>b/(s-1)时，P_n是钟形分布。若sa/(a+b)=1，即a=b/(s-1)，则P₁=P₀。等式(11)意味着当正反馈强度μ充分大时，对所有的n≥2，有P_n>P_n-1。因此当正反馈强度μ充分大且a=b/(s-1)时，P_n是单峰分布。(Ⅰ)得证。若sa/(a+b)<1，即a<b/(s-1)，则P₁<P₀。等式(11)意味着当μ>μ^*时，对所有的n≥2，有P_n>P_n-1。因此当μ>μ^*且a<b/(s-1)时，P_n是双峰分布。(Ⅱ)得证。

定理6表明当负反馈强度ν充分大时，P_n不会产生钟形分布。定理7则表明当正反馈强度μ充分大时，P_n不会产生递减分布，并且双峰分布始终存在。

4　结论与小结

在本文中，我们考虑了一个耦合最小正负反馈回路、基因随机切换、蛋白质的生成与降解的随机基因表达模型。该模型在稳态时化学主方程已被求解出来^[22,23]，其解含有两个合流超几何函数。因此想直接通过解的解析式判断它的分布形态是极其困难的。文献[20]首次用数学的语言严格证明了两状态模型只能产生递减分布、钟形分布或双峰分布，并通过构建两条曲线C₁和C₂将参数平面划分为与三种分布形态一一对应的三个区域，进而得到产生这三种分布形态的充分必要条件。文献[21]则在文献[20]的基础上，将两状态模型推广到带有正负反馈的最小耦合基因模型，同样也通过构建两条曲线C₁和C₂得到产生这三种分布形态的充分必要条件。然而，曲线C₁和C₂并没有相应的显示表达式，因此，直接且快速地判断某组参数集所产生的分布形态是困难的。本文给出了若干产生递减分布、钟形分布和双峰分布的充分条件。这些条件能够帮助我们直接快速地判断P_n的分布形态。其次我们还考虑了当正反馈或负反馈充分大时对分布形态的影响，发现当正反馈足够大时，P_n要么是双峰分布，要么是钟形分布;当负反馈足够大时，P_n不会产生双峰分布。值得注意的是，本文考虑的模型能退化成两状态模型、正反馈模型或负反馈模型，因此本文的所有结论都适用于这些模型。

利益冲突: 作者声明没有利益冲突。

---

^[②] *通讯作者　Corresponding author:焦锋，jiaof@gzhu.edu.cn
收稿日期:2025-02-01;　录用日期:2025-02-10;　发表日期:2025-03-28

参考文献(References)

[1] Lee T I, Young R A. Transcriptional regulation and its misregulation in disease[J]. Cell, 2013, 152(6): 1237-1251.
https://doi.org/10.1016/j.cell.2013.02.014.
[2] Hamaneh M B, Yu Y K. Relating diseases by integrating gene associations and information flow through protein interaction network[J]. PLoS One, 2014, 9(10): e110936.
https://doi.org/10.1371/journal.pone.0110936.
[3] Kaern M, Elston T C, Blake W J, et al. Stochasticity in gene expression: from theories to phenotypes[J]. Nat Rev Genet, 2005, 6(6): 451-464.
https://doi.org/10.1038/nrg1615.
[4] Sweatt A J, Griffiths C D, Groves S M, et al. Proteomewide copy-number estimation from transcriptomics[J]. Mol Syst Biol, 2024, 20(11): 1230-1256.
https://doi.org/10.1038/s44320-024-00064-3.
[5] Harshbarger B, Feller W. An Introduction to Probability Theory and Its Applications[J]. Volume I. AIBS Bulletin, 1958, 8(1): 32.
https://doi.org/10.1137/1011021.
[6] Davidson E H. The regulatory genome: gene regulatory networks in development and evolution[M]. Elsevier, 2010.
https://doi.org/10.1016/B978-0-12-088563-3.X5000-8.
[7] Shen Orr S S, Milo R, Mangan S, et al. Network motifs in the transcriptional regulation network of Escherichia coli[J]. Nat. Genet, 2002, 31: 64-68.
https://doi.org/10.1038/ng881.
[8] Rosenfeld N, Elowitz M B, Alon U. Negative autoregulation speeds the response times of transcription networks[J]. J. Mol. Biol, 2002, 323: 785-793.
https://doi.org/10.1016/s0022-2836(02)00994-4.
[9] Friedman N, Cai L, Xie X S. Linking stochastic dynamics to population distribution: an analytical framework of gene expression[J]. Phys. Rev. Lett, 2006, 97: 168302.
https://doi.org/10.1103/PhysRevLett.97.168302.
[10] Mackey M C, Tyran-Kaminska M, Yvinec R. Dynamic behavior of stochastic gene expression models in the presence of bursting[J]. SIAM J. Appl. Math, 2013, 73: 1830-1852.
https://doi.org/10.1137/12090229X.
[11] Bokes P, Singh A. Protein copy number distributions for a self-regulating gene in the presence of decoy binding sites[J]. PloS one, 2015, 10: e0120555.
https://doi.org/10.1371/journal.pone.0120555.
[12] Munsky B, Neuert G, Van Oudenaarden A. Using gene expression noise to understand gene regulation[J]. Science, 2012, 336: 183-187.
https://doi.org/10.1126/science.1216379.
[13] Venturelli O S, El-Samad H, Murray R M. Synergistic dual positive feedback loops established by molecular sequestration generate robust bimodal response[J]. Proc Natl Acad Sci, 2012, 109(48): E3324-3333.
https://doi.org/10.1073/pnas.1211902109.
[14] Choi P J, Cai L, Frieda K, et al. A stochastic single-molecule event triggers phenotype switching of a bacterial cell[J]. Science, 2008, 322(5900): 442-446.
https://doi.org/10.1126/science.1161427.
[15] Liu P, Yuan Z, Huang L, et al. Roles of factorial noise in inducing bimodal gene expression[J]. Phys Rev E Stat Nonlin Soft Matter Phys, 2015, 91(6): 062706.
https://doi.org/10.1103/PhysRevE.91.062706.
[16] Hornos J E M, Schultz D, Innocentini G C P, et al. Selfregulating gene: an exact solution[J]. Phys. Rev. E, 2005, 72: 051907.
https://doi.org/10.1103/PhysRevE.72.051907.
[17] Grima R, Schmidt D R, Newman T J. Steady-state fluctuations of a genetic feedback loop: An exact solution [J]. J. Chem. Phys, 2012, 137(3): 035104.
https://doi.org/10.1063/1.4736721.
[18] Kumar N, Platini T, Kulkarni R V. Exact distributions for stochastic gene expression models with bursting and feedback[J]. Phys. Rev. Lett, 2014, 113: 268105
https://doi.org/10.1103/PhysRevLett.113.268105.
[19] Jia C, Grima R. Small protein number effects in stochastic models of autoregulated bursty gene expression[J]. J. Chem. Phys, 2020, 152(8): 084115.
https://doi.org/10.1063/1.5144578.
[20] Jiao F, Sun Q, Tang M, Yu, et al. Distribution modes and their corresponding parameter regions in stochastic gene transcription[J]. SIAM J. Appl. Math, 2015, 75: 2396-2420.
https://doi.org/10.1137/151005567.
[21] Sheng Y, Lin G, Jiao F, et al. Geometric theory of distribution shapes for autoregulatory gene circuits[R]. To appear in SIAM Journal on Applied Mathematics, 2024.
https://doi.org/10.1101/2024.04.02.587730
[22] Liu P, Yuan Z, Wang H, et al. Decomposition and tunability of expression noise in the presence of coupled feedbacks[J]. Chaos, 2016, 26: 043108.
https://doi.org/10.1063/1.4947202.
[23] Jia C, Yin G G, Zhang M Q, et al. Single-cell stochastic gene expression kinetics with coupled positive-plusnegative feedback[J]. Phys. Rev. E, 2019, 100: 052406.
https://doi.org/10.1103/PhysRevE.100.052406.
[24] Frank W J, Olver, Daniel W L, et al. NIST Digital Library of Mathematical Functions[J]. Annals of Mathematics and Artificial Intelligence, 2003, 38: 105-119.
https://doi.org/10.1023/A:1022915830921

The Discriminative Conditions for the Distribution Pattern of Expression Products in Stochastic Gene Expression Models

QIU Zhishan, SHENG Ying, JIAO Feng^*

(School of Mathematics and Information Sciences, Guangzhou University, Guangzhou 510006, China)

Abstract: Gene expression is essentially a random process. The distribution of expression product quantities can comprehensively describe the stochastic behavior. of gene expression, which typically exhibits three distribution shapes: decaying, bell-shaped, and bimodal. Ref. [21] explores a stochastic gene expression model of minimal coupled positive-plus-negative feedback loop. By constructing two continuous curves C1 and C2 in the parameter phase, the necessary and sufficient conditions for the model to generate three distribution shapes were theoretically provided. However, for any given set of parameters, since the curves C1 and C2 cannot give exact expressions, it is difficult to directly and quickly determine which distribution shape the stochastic gene expression model of a minimal coupled positive-plus-negative feedback loop can generate. This greatly affects our research on massive single cell transcriptomic data using mathematical models. In this paper, we present several system parameter conditions that generate the three distribution shapes by quantitatively characterizing the curves C1 and C2. These parameter conditions can be calculated using simple elementary functions. Thus, a rapid discrimination method for determining the distribution shape of the quantity of expression products in the stochastic gene expression model is provided.  

Keywords: Stochastic gene transcription model, positive-plus-negative feedback loop, chemical response master equation, quantitative distribution of expression products

DOI: 10.48014/jcss.20250201001

Citation: QIU Zhishan, SHENG Ying, JIAO Feng. The discriminative conditions for the distribution pattern of expression products in stochastic gene expression models[J]. Journal of Chinese Statistical Sciences, 2025, 3(1): 15-25.