

阀式磁流变阻尼器中磁流变液流动状态多物理场模拟
(1. 大连理工大学 材料科学与工程学院, 大连 116024
2. 海军潜艇学院, 青岛 266199
3. 大连理工大学 土木工程学院, 大连 116024
4. 海南大学 土木建筑工程学院, 海口 570228)
摘要: 磁流变液 (Magnetorheological fluid, MRF) 作为一种磁场响应型的智能流体, 在阻尼减振领域受到广泛关注。MRF的流动状态对阻尼器中的振动控制起到关键作用。本文通过多物理场模拟对MRF在阀式阻尼器中的流动行为进行了研究, 目的在于全面的了解磁场如何改变沿磁流变阻尼器通道内MRF的速度分布和压降。通过创建通电线圈实现磁场的产生, 随后通过调整电流改变磁通密度。磁场计算表明, 在阻尼器流道最窄处, 磁场几乎垂直于MRF流动方向。接着, 基于流体流动、电场以及磁场间的多物理场耦合计算, 计算分析了不同磁场下MRF在流道中的流速变化以及压力等特性。结果表明, 在MRF流动方向垂直于磁场方向的流道最窄处, MRF的流动使其受到体积力, 进而使流速出现降低的趋势, 在流道左右两侧产生较大压力差。此外, MRF的流速随磁场的增大而减小, 磁场强度从0. 5T增加到1. 5T时, MRF流体在流道最窄处的流速降低大约0. 18m/s。
DOI: 10.48014/pcms.20231118001
引用格式: 赵鹏慧, 曾帆, 马宁, 等. 阀式磁流变阻尼器中磁流变液流动状态多物理场模拟[J]. 中国材料科学进展, 2024, 3(1): 12-19.
文章类型: 研究性论文
收稿日期: 2023-11-18
接收日期: 2023-12-17
出版日期: 2024-03-28
0 引言
1948年Rabinow首先提出了磁流变液(Magnetorheological fluid,MRF)的概念[1],MRF是由可磁化的磁性颗粒和不可磁化的载液构成的悬浮液[2],在外加磁场作用下会在毫秒间由近似牛顿流体快速转变成类固体的结构[3]。在此过程中,MRF的屈服应力、黏度等都会显著增大,当撤去磁场后又可以快速恢复到流体状态[4]。凭借在磁场下的快速响应、阻尼力可调以及低能量需求等优点,MRF已经在阻尼减振、旋转密封、生物医疗等工程技术领域受到广泛关注[5-8]。
近年来,计算机模拟技术因在探索MRF微观尺度上的结构与力学行为表现出重要作用,已成为MRF理论与实际应用研究中非常重要的一环。Liu[9]等提出了一种具有高精度的双网格双分量点阵玻尔兹曼方法,采用该方法对MRF中磁性粒子在磁场作用下从分散状态到链状结构的聚集过程进行了计算分析。为了从微观结构探究颗粒形貌对MRF聚集结构的影响,Satoh等[10,11]采用蒙特卡罗法研究了磁场作用下圆盘状及棒状磁性粒子的聚集结构,结果表明不同形状的磁性粒子在磁场作用下的聚集行为表现出较大的差异,其中圆盘状颗粒在磁场下具有更紧密的堆叠结构。Peng等[12]基于布朗动力学方法对外加磁场下MRF结构的相分离,链状结构尺寸统计以及聚集结构的各向异性进行了模拟分析。研究证明磁场强度越大,结构相分离的时间越短。磁性颗粒在磁场下的聚集结构随着剪切场流动并组成片状聚集结构,以抑制剪切流的作用。中国科学技术大学裴雷[13-15]等在磁偶极子模型的基础上,对磁性颗粒间弹性挤压力以及切向摩擦力的作用进行数学建模,将这两种作用力引入MRF的粒子级模拟中。该研究首次揭示了MRF微观结构与颗粒摩擦系数(μ)之间的关系,并提出摩擦系数的最佳范围为2≤μ≤2.75。在宏观模拟方面,针对MRF在工程领域的应用,科研人员主要对MRF阻尼器进行了有限元仿真设计,以实现辅助设计具有不同功能的器件或者优化结构的目的。Maurya等[16]通过数值模拟证明磁流变仪在MRF测试区的磁通密度和温度分布最为均匀,在3安培的通电线圈下可产生1.1 T的最大磁通密度。为控制管道振动,Xin等[17]设计了一种剪切阀型磁流变阻尼器,计算了最优阻尼力,并采用有限元方法对阻尼器的磁场和电磁热场进行仿真,确保阻尼器的温度和磁场满足实际工作条件。
综上所述,目前MRF的理论研究主要集中于介观尺度的磁致取向结构和宏观尺度下MRF阻尼器中的磁场分布。事实上,磁场作用下MRF在阻尼器等结构中的流动状态对研究磁流变阻尼器的工作特点,制作高性能MRF器件有重要参考价值。因此,我们基于磁流体动力学,研究了电磁场与流场耦合下不可压缩MRF在通过阀式阻尼器孔道中的流动行为进行了模拟研究。
1 模型与理论
1.1 模型构建
MRF阀式阻尼器是MRF应用中较为广泛的一种,在这种模式中,MRF压力流在磁极间流动,通过COMSOL软件建立与实际MRF阻尼器相匹配的二维几何模型,如图1所示。在模拟过程中,令MRF从左侧端口流入,右侧端口流出,中间经过缸壁与通电线圈之间的流道。当通电线圈产生磁场时,流道中的MRF由于磁流变效应而转变为类固体结构而产生屈服应力和压力差。另一方面,在这类型MRF装置中,MRF不断穿过内部的各流道时,由于流体动量方程中与磁场存在而产生的外力所导致MRF速度减小而产生压降,进而产生屈服作用。在本模型中,缸壁和活塞均为导磁材料,相对磁导率设置为2000。
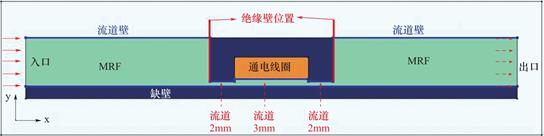
图1 MRF阻尼器中MRF流动模拟二维几何模型
Fig.1 A two-dimensional geometric model for MRF flow simulation in MRF dampers
1.2 多物理场耦合
本文对磁场下MRF在阻尼器中的流动状态进行了有限元模拟研究,这涉及到了流体流动、电流以及磁场间的多物理场耦合,不同的物理场对应不同的偏微分方程,这些方程可通过有限元方法求解。当MRF中颗粒体积分数为30%~40%时,MRF流动和磁性颗粒的运动之间几乎没有区别。基于这种情况,在磁流体动力学中,每个磁性颗粒视为流体颗粒,磁性颗粒之间的任何相互作用,如磁性粒子的转动、内部磁力或碰撞都不被考虑在内[18],MRF表现为稳定连续的不可压缩单相流体。另一方面,根据MRF的组成可知,载液通常为硅油等不导电介质,而磁性颗粒则是良导体。基于磁性颗粒连续介质假设,由于磁粒的存在,在磁流体动力学中MRF整体上视作是良导体。如果它在磁场中运动,就会产生电流,从而在MRF中产生一种新的力,即洛伦兹力。因此,本文对MRF在磁场下的流动状态研究基于磁性颗粒连续体假设和连续介质下MRF导电的假设。
经过上述的分析假设可知,MRF流体流场与电磁场之间的耦合源于MRF在磁场中运动而产生感应电流,以及MRF中感应电流和磁场间产生的洛伦兹力。而感应电流所导致的洛伦兹力表现出与产生它们的作用而相反的效果。这将导致MRF在磁场中的往复运动被由此产生的洛伦兹力所破坏。
在模拟中,整个MRF阻尼器内的电磁场分布可以通过麦克斯韦方程组表示:
Ñ×H=J(1)
B=Ñ×A(2)
E=-![]() (3)
(3)
式中,Ñ是哈密顿算符,J是电流密度,B和E分别为磁场和电场,A表示磁势。
MRF流体以一定速度v移动通过通电线圈产生的磁场B,从而产生感应电流J。因此,对于磁场B中的速度场为v的MRF,电流密度J表示为:
J=σ![]() (4)
(4)
式中,![]() 为电导率。磁场和流场耦合下,MRF受到的体积力F表示为:
为电导率。磁场和流场耦合下,MRF受到的体积力F表示为:
F=J×B(5)
此外,还需要求解通道中的流场。在模拟中,MRF被认为是稳定的层流,从而在通道域中求解纳维-斯托克斯方程。
ρ![]() +ρ
+ρ![]() v=Ñ·
v=Ñ·![]() +F+ρg(6)
+F+ρg(6)
ρÑ·v=0(7)
K=μ![]() (8)
(8)
式中ρ,v,μ分别表示流体密度,速度矢量和动态黏度。p,I,g分别表示压力场,单位矩阵以及重力场。F表示MRF流动过程中受到的洛伦兹力,即体积力。
1.3 网格划分
在有限元模型中,将整个求解域看作由大量微小互连子域组成的结构,这些子域被称为单元(网格)。一般来说,网格划分的精密度决定了区域求解的精确性,但是随着网格尺寸的减小,计算成本将大幅增加。因此,在有限元模型网格划分时,不同位置的网格细化程度也不同。在位移梯度较大或者需要较高精度的区域网格划分更加精细,而边缘位置网格较大。基于此,本研究中MRF在阻尼器中流动模拟结构的网格划分如图2所示。将模拟区域划分为大量的三角形单元,对相邻区域的边界处进行更精细的网格划分,整个区域中网格介于0.4mm~14mm之间,其中MRF流动模拟区域网格尺寸约0.4mm~2mm。网格划分后,设置MRF模拟参数,如表1所示。最后,对设置好的模型进行有限元计算,求解在历时10s的时间范围内MRF的瞬态流动。

图2 模拟区域有限元网格划分
Fig.2 Finite element mesh division of simulation area
表1 模拟参数
Table 1 Simulation parameter
|
项目 |
φ |
ρ/(kg/m3) |
η/(kg/ms) |
μr |
σ/(S/m) |
d/mm |
l/mm |
p0/Pa |
|
数值 |
20% |
2380 |
0.050 |
4 |
3.46·104 |
2 |
50 |
5000 |
|
描述 |
磁性颗粒 体积分数 |
MRF 密度 |
MRF 黏度 |
MRF相对 磁导率 |
MRF 电导率 |
流道最 窄宽度 |
流道 长度 |
入口 压力 |
2 结果与讨论
2.1 磁路分析
模拟中磁场由通电线圈产生[19,20],导线的直径为0.8mm,线圈匝数为500,接入电流为2A,经过有限元计算得到如图3所示的磁通密度分布。因为MRF沿着x方向在孔道中流动,因此我们只显示了在y方向通过流道处的磁通密度分布以及磁场线穿过狭缝处的情况。从图中可以看出,电流为2A时,在流道最窄处可产生近1.0T的磁场,在MRF阻尼器内形成了闭合磁路。另外,由于在活塞架两端设置了绝缘壁,可以在一定程度上改善MRF阻尼器内磁感线的分布,使得流道最窄处磁感线分布较为均匀,方向几乎与y轴平行。因此,从磁通密度和磁感线分布可知,该模型的输入电流以及产生的磁场与MRF阻尼器的实际情况较为接近,模拟设置可以较好地反映MRF阻尼器的真实情况[21,22]。
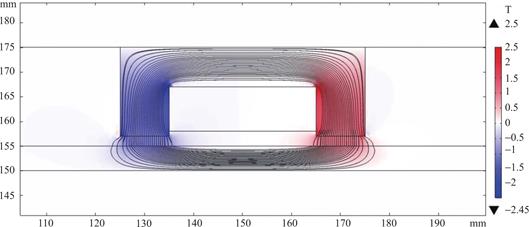
图3 MRF阻尼器中磁通密度和磁感线分布
Fig.3 Magnetic flux density and magnetic induction line distribution in MRF dampers
2.2 体积力与压力
本研究中,令MRF以压力流的方式从流道中通过,MRF的初速度为0,将MRF入口端的压力和出口端压力分别设置为5000Pa和0Pa。流体流经流道最狭窄处时,由于此处磁场几乎与流体流动方向垂直,所以MRF必然受到洛伦兹力。图4表示狭缝处磁场为0.5T和1.0T时,MRF在流道中受到的体积力。从图中可以看到,MRF在狭缝处受到与与其流动方向相反的体积力(洛伦兹力),且随着狭缝处磁场的增大,MRF受到的力也显著增大,这将对MRF在阻尼器中的正常流动产生影响[23,24]。
接下来我们计算了MRF在阻尼器中的压力情况。图5(a)为模拟初始时刻系统中MRF的压力云图,可以发现在流道左侧的腔体里面,MRF的压力为0,而由于中间狭窄流道(仅2~3mm)的存在,MRF的自然流动受限,右侧腔体则压力出现的负值,在开始阶段这是正常的现象,如果流道的宽度较大则两侧腔体的压力都将趋于0。随着MRF在左端入口处加载压力后,体系中MRF的压力开始发生变化,如图5(b)。由于MRF受到磁场的作用,在经过左侧流道最窄处时受到阻碍作用,在流道中压力梯度变化急剧增大,因此两个腔体出现显著的压力差,右侧腔室压力变得更小。
2.3 流速
图6为通电线圈电流为2A产生磁场下,系统中不同时刻MRF的流速与流线分布情况,此时流道狭缝处磁场为1.0T。由图可知,在模拟初始时刻(t=0),MRF的流速几乎接近于0。随着时间推移,在压力推动下MRF开始向出口端流动,经过流道时流速明显增大,从流道右边出来后,MRF以喷射状流出,并产生了较为明显的漩涡,这也说明MRF经过流道从右侧的狭缝中流出时存在较大压力差。
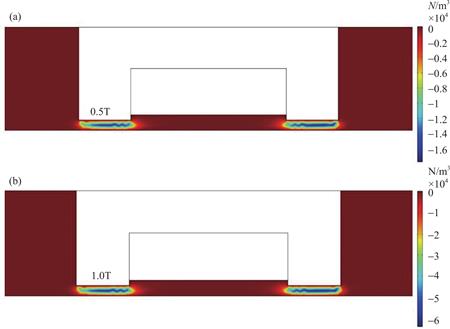
图4 磁场下MRF流动时受到的体积力
Fig.4 Volume force acting on MRF flow under magnetic field

图5 MRF阻尼器中不同时刻MRF的压力
Fig.5 Pressure of MRF at different times in MRF dampers
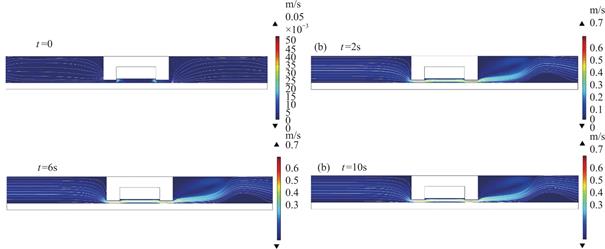
图6 不同时刻MRF的流速和流线分布
Fig.6 Flow velocity and streamline distribution of MRF at different times
为了进一步考察磁场强度对MRF流速的影响,在500匝的通电线圈中接入1A、2A、3A的电流,令流道最窄处分别产生0.5T、1.0T以及1.5T的磁场(还可以改变通电线圈的匝数来调节磁场)。同样在左侧入口处施加5000Pa的压力,令MRF从右侧流出。然后我们通过域点探针监测了左侧流道最窄处MRF流速的变化情况,如图7所示。从图中可以看出MRF的流速随着磁场的增加流道最窄处的流速逐渐减小,0.5T时狭缝处的流速为0.74m/s,当磁场增加到1.5T时,降低到了0.56m/s。这种变化特点表明MRF的流动会受到磁场的影响,而这种影响的来源是体积力。
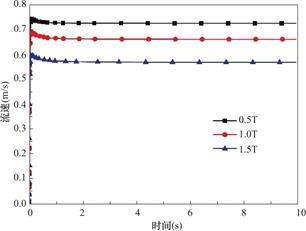
图7 不同磁场强度下MRF的流速对比
Fig.7 Velocity of MRF at different magnetic fields
进一步,我们固定通电线圈的电流为3A,将线圈匝数增加到2000,此时流道最窄处的磁场高达6.0T,在日常生活中如此高的磁场是罕见的,我们仅用该强度磁场说明磁场对MRF流动性的影响。在这种极强磁场下,MRF的流动如图8所示。结果表明,与0.5T~1.5T磁场下的MRF流动相比,强磁场下流道最窄处MRF的流速急剧降低到0.07m/s。不难想象,当磁场强度继续增大,MRF将处于停滞状态。表明调节磁场可以控制MRF的流动速度[25,26],进而调控其在阀模式下的流动行为。
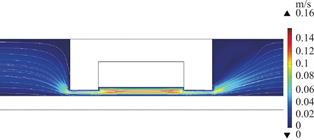
图8 强磁场下阻尼器中MRF的流速和流线分布
Fig.8 Velocity and streamline distribution of MRF in dampers under high magnetic fields
3 结论
本文在电磁场与流体流动方程耦合下,对MRF在阀式阻尼器中的流动行为进行了多物理场模拟,磁场由通电线圈产生磁场,MRF流体为不可压缩的黏性单相流。经过有限元计算,得到了MRF在阻尼器中流动时受到的洛伦兹力、压力以及随着时间变化的流速情况,揭示了MRF在压力驱动下的流动行为。结果表明,磁场作用于MRF时,MRF的流速随磁场的增大而减小。当流道最窄处的磁通密度达到6.0T的极强磁场时,MRF的流动将非常微弱,处于几乎停止的状态这将进一步导致在流道左右的腔室产生较大的压力差。磁场下MRF流动状态的改变是由于其作为导电流体在流经磁场时受到洛伦兹力的作用。本研究采用的多物理场耦合方法可以为模拟MRF在更复杂器件中的流动问题提供了一个有意义的参考。
利益冲突: 作者声明无利益冲突。
[②] *通讯作者 Corresponding author:董旭峰,dongxf@dlut.edu.cn
收稿日期:2023-11-18; 录用日期:2023-11-17; 发表日期:2024-03-28
基金项目:本项研究得到了国家自然科学基金项目(资助号52178459和52008016)的资助。
参考文献(References)
[1] Rabinow J. The magnetic fluid clutch[J]. Electrical Engineering, 1948, 67(12): 1167-1167.
https://doi.org/10.1109/EE.1948.6444497
[2] Zhou J, Mo J, Shao C, et al. Effects of magnetized walls on the particle structure and the yield stress of magnetorheological fluids[J]. Journal of Magnetism & Magnetic Materials, 2015, 389: 124-129.
https://doi.org/10.1016/j.jmmm.2015.03.088
[3] De Vicente J, Klingenberg D J, Hidalgoalvarez R. Magnetorheological fluids: a review[J]. Soft Matter, 2011, 7(8): 3701-3710.
https://doi.org/10.1039/C0SM01221A
[4] 江泽琦, 刘坪, 方建华. 磁流变液的研究综述[J]. 合成润滑材料, 2018, 45(2): 27-30.
https://doi.org/10.3969/j.issn.1672-4364.2018.02.010
[5] Liu G, Gao F, Wang D, et al. Medical applications of magnetorheological fluid: A systematic review[J]. Smart Materials and Structures, 2022, 31(4): 043002.
https://doi.org/10.1088/1361-665X/ac54e7
[6] 郭朝阳, 黎剑锋, 薛群, 等. 内通道式磁流变阻尼器研究[J]. 实验力学, 2008, 23(06): 485-490.
[7] 阮晓辉, 边会婷, 赵军, 等. 用于提高剪力墙性能的大尺度磁流变阻尼器的力学性能研究[J]. 实验力学, 2020, 35(05): 759-770.
https://doi.org/10.7520/1001-4888-19-199
[8] 丁欢, 韩光辉, 邓华夏, 等. 视觉引导的磁流变振动控制方法[J]. 实验力学, 2021, 36(04): 491-498.
https://doi.org/10.7520/1001-4888-20-207
[9] Liu X, Liu H, Liu Y. Simulation of magnetorheological fluids based on Lattice Boltzmann method with double meshes[J]. Journal of Applied Mathematics, 2012, 2012: 1-16.
https://doi.org/10.1155/2012/567208
[10] Satoh A, Aoshima M. 3D Monte Carlo simulations of a magnetic disk-like particle dispersion[J]. Colloid & Polymer Science, 2011, 289(1): 53-62.
https://doi.org/10.1007/s00396-010-2320-9
[11] Satoh A. Monte Carlo simulations on phase change in aggregate structures of ferromagnetic spherocylinder particles[J]. Colloids & Surfaces A Physicochemical & Engineering Aspects, 2016, 504: 393-399.
https://doi.org/10.1016/j.colsurfa.2016.05.081
[12] Peng Y B, Ghanem R, Li J. Investigations of microstructured behaviors of magnetorheological suspensions[J]. Journal of Intelligent Material Systems & Structures, 2012, 23(12): 1351-1370.
https://doi.org/10.1177/1045389X12447288
[13] Pei L, Xuan S, Wu J, et al. Experiments and simulations on the magnetorheology of magnetic fluid based on Fe3O4 hollow chains[J]. Langmuir, 2019, 35(37): 12158-12167.
https://doi.org/10.1021/acs.langmuir.9b01957
[14] Pei L, Xuan S, Pang H, et al. Influence of interparticle friction on the magneto-rheological effect for magnetic fluid: a simulation investigation[J]. Smart Materials and Structures, 2020, 29(11): 115002.
https://doi.org/10.1088/1361-665X/ababe3
[15] Pei L, Ma Z, Ma D, et al. Simulations on the rheology of dry magneto-rheological fluid under various working modes[J]. Smart Materials and Structures, 2021, 31(1): 015031.
https://doi.org/10.1088/1361-665x/ac36ad
[16] Maurya C S, Sarkar C. Magnetic and transient temperature field simulation of plate-plate magnetorheometer using finite-element method[J]. IEEE Transactions on Magnetics, 2020, 56(4): 1-9.
https://doi.org/10.1109/tmag.2019.2960237
[17] De-kui X, Song-lin N, Hui J, et al. Characteristics, optimal design, and performance analyses of MRF damper[J]. Shock and Vibration, 2018, 2018(PT. 6): 64549321. 1-6454932. 17.
https://doi.org/10.1155/2018/6454932
[18] Llorente V J, Pascau A. Numerical simulations of magnetorheological fluids flowing between two fixed parallel plates[J]. Applied Mathematical Modelling, 2019, 74: 151-169.
https://doi.org/10.1016/j.apm.2019.04.047
[19] 王金刚, 王治国. 磁流变阻尼器阻尼性能仿真研究[J]. 石油机械, 2006(10): 19-22+1.
https://doi.org/10.3969/j.issn.1001-4578.2006.10.007
[20] 赵玉亮, 徐赵东, 许飞鸿. 基于全构件模型的磁流变阻尼器磁路分析及测试[J]. 东南大学学报(自然科学版), 2017, 47(03): 565-570.
https://doi.org/10.3969/j.issn.1001-0505.2017.03.025
[21] 李国全, 黄子齐, 陈俊杰. 磁流变液制备及其流动特性有限元仿真[J]. 机电工程技术, 2023, 52(09): 84-88.
https://doi.org/10.3969/j.issn.1009-9492.2023.09.018
[22] 许飞鸿, 徐赵东. 多级线圈磁流变阻尼器磁路分析[J]. 东南大学学报(自然科学版), 2016, 46(01): 100-104.
https://doi.org/10.3969/j.issn.1001-0505.2016.01.017
[23] Gedik E, Kurt H, Recebli Z, et al. Two-dimensional CFD simulation of magnetorheological fluid between two fixed parallel plates applied external magnetic field[J]. Computers & fluids, 2012, 63: 128-134.
https://doi.org/10.1016/j.compfluid.2012.04.011
[24] Szabo P S B, Frueh W G. The transition from natural convection to thermomagnetic convection of a magnetic fluid in a non-uniform magnetic field[J]. Journal of Magnetism and Magnetic Materials, 2018, 447: 116-123.
https://doi.org/10.1016/j.jmmm.2017.09.028
[25] Kemerli M, Engin T. Numerical analysis of a monotube mixed mode magnetorheological damper by using a new rheological approach in CFD[J]. Rheologica Acta, 2021, 60(1): 77-95.
https://doi.org/10.1007/s00397-020-01252-2
[26] Zhang S, Zhou J, Shao C. Numerical investigation on yielding phenomena of magnetorheological fluid flowing through microchannel governed by transverse magnetic field[J]. Physics of Fluids, 2019, 31(2): 022005.
https://doi.org/10.1063/1.5079624
Multi-Physical Field Simulation of Magnetorheological Fluid Flow State in Valve Magnetorheological Damper
(1. School of Materials Science and Engineering, Dalian University of Technology, Dalian 116024, China
2. Naval Submarine Academy, Qingdao 266199, China
3. School of Civil Engineering, Dalian University of Technology, Dalian 116024, China
4. School of Civil Engineering, Hainan University, Haikou 570228, China)
Abstract: Magnetorheological fluid (MRF) is a kind of magnetic field responsive intelligent fluid, which is widely concerned in the field of damping and vibration reduction. The flow state of MRF plays a key role in vibration control in dampers. In this work, the flow behavior. of magnetorheological fluid (MRF) in a valve damper is studied through multi-physical field simulations. The objective is to comprehensively comprehend the influence of the magnetic field on the velocity distribution and pressure drop of the MRF within the damper channel. The magnetic field is generated by creating an electrified coil, and the magnetic flux density is subsequently changed by adjusting the current. The magnetic field calculation shows that the magnetic field is almost perpendicular to the MRF flow direction at the narrowest part of the damper channel. Next, based on the coupling calculation of multiple physical fields between fluid flow, electric field, and magnetic field, the flow velocity and pressure characteristics of MRF in the flow channel were calculated and analyzed. The results indicate that at the slit where the MRF flow direction is perpendicular to the magnetic field direction, the volume force acting on the MRF reduces its flow velocity, resulting in a significant pressure difference between the left and right sides of the flow channel. Additionally, the flow rate of MRF exhibits a decrease as the magnetic field strength increases. When the magnetic field strength increases from 0. 5T to 1. 5T, the flow rate of MRF fluid at the narrowest part of the flow channel decreases by about 0. 18m/s.
Keywords: Damper, magnetorheological fluid, flow state, multi-physical field
DOI: 10.48014/pcms.20231118001
Citation: ZHAO Penghui, ZENG Fan, MA Ning, et al. Multi-physical field simulation of magnetorheological fluid flow state in valve magnetorheological damper[J]. Progress in Chinese Materials Sciences, 2024, 3(1): 12-19.